众所周知,懒标记是线段树解决区间更新问题的利器。
本人学习懒标记的时候,找了网上一大堆博客看,但是少有人解释具体细节,导致浪费了很多时间才彻底理解。
好了,回顾一下整个过程:区间更新时,我们递归查找目标区间的子区间,过程中不断维护当前节点的信息(要求的信息,比如区间和),每找到一个目标区间的子区间(有可能只有1个点)被完全覆盖到时停止往下递归。最妙的地方在于我们每次不必要把懒标记下传到底,只需传到管理目标区间的子区间的节点就行,下次再有更新的时候,我们再随着更新递归传递标记就好了。注意,递归时我们不仅要把当前懒标记的信息传递下去还要重置懒标记,具体为什么后面解释。
以hdu-1698为例,q次操作,将某一个区间[x,y]内所有的数置为z,最后查询区间总和。
假设n=4,首先建树维护初始区间和,s数组表示区间,x数组表示懒标记,如下图所示:

然后我们执行两次更新操作:
更新[1,2]为2;
更新[2,3]为3;
我们先不用执行down函数即不下传懒标记,查询结果:

可以发现4号节点的sumv错误,应该为2,由此导致2号节点的sumv也错误,原因是更新[2,3]为3时没有把2号节点的懒标记传下给4号和5号。
再来看下执行down函数传递懒标记之后的正确结果:

ok,看到这里你大概已经意识到了传递懒标记的必要性。
我们都知道每次传递懒标记后自身的要重置,直觉告诉我们这是必要的,我们不妨也来个例子证明一下下:
我们执行三次更新操作:
更新[1,2]为2;
更新[2,2]为3;
更新[1,1]为3;
先不重置懒标记,看下结果是怎样:
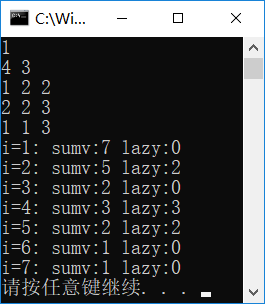
发现5号节点的sumv错误,应该是3才对!
这是因为2号的lazy我们没有重置为0,导致在更新[1,1]时把5号节点的sumv(本来是3)置为了2。
再来看下重置懒标记后的正确结果:

附上这题的AC兼测试代码:
1 #define dbg(x) cout<<#x<<" = "<< (x)<< endl 2 #define IO std::ios::sync_with_stdio(0); 3 #include <bits/stdc++.h> 4 #define iter ::iterator 5 using namespace std; 6 typedef long long ll; 7 typedef pair<ll,ll>P; 8 #define pb push_back 9 #define se second 10 #define fi first 11 #define rs o*2+1 12 #define ls o*2 13 const ll inf=0x7fffffff; 14 const int N=1e5+5; 15 int sumv[N*4],setv[N*4]; 16 void build(int o,int l,int r){ 17 setv[o]=0; 18 if(l==r){ 19 sumv[o]=1; 20 return; 21 } 22 int m=(l+r)/2; 23 build(ls,l,m); 24 build(rs,m+1,r); 25 sumv[o]=sumv[ls]+sumv[rs]; 26 } 27 void down(int o,int l,int r){ 28 if(!setv[o])return; 29 int m=(l+r)/2; 30 setv[ls]=setv[rs]=setv[o]; 31 sumv[ls]=setv[ls]*(m-l+1); 32 sumv[rs]=setv[rs]*(r-m); 33 setv[o]=0; 34 } 35 void up(int o,int l,int r,int ql,int qr,int v){ 36 if(l>=ql&&r<=qr){ 37 sumv[o]=v*(r-l+1); 38 setv[o]=v; 39 return; 40 } 41 down(o,l,r); 42 int m=(l+r)/2; 43 if(ql<=m)up(ls,l,m,ql,qr,v); 44 if(qr>m)up(rs,m+1,r,ql,qr,v); 45 sumv[o]=sumv[ls]+sumv[rs]; 46 } 47 int T,n,q; 48 int main(){ 49 scanf("%d",&T); 50 int kase=0; 51 while(T--){ 52 scanf("%d%d",&n,&q); 53 build(1,1,n); 54 while(q--){ 55 int x,y,z; 56 scanf("%d%d%d",&x,&y,&z); 57 up(1,1,n,x,y,z); 58 } 59 //for(int i=1;i<=7;i++)printf("i=%d: sumv:%d lazy:%d ",i,sumv[i],setv[i]); 60 printf("Case %d: The total value of the hook is %d. ",++kase,sumv[1]); 61 } 62 } 63 /* 64 1 65 4 2 66 1 2 2 67 2 3 3 68 69 1 70 4 3 71 1 2 2 72 2 2 3 73 1 1 3 74 75 */
看到这里,宣告线段树懒标记彻底拿下,但是线段树花样多,还是要靠大量刷题才能完全掌握。具体可以参考本人刷过的线段树专题,直接点击右边线段树标签即可。