Prologue
令人遗憾的是,我的讲解可能很抽象。
也可以参考 Topcoder 的 Competitive-Programming 教程 -> [Click Here]
或者 OI Wiki 的教程,左边 Menu 可以快速跳转。
树状数组是什么?它可以维护一个序列。
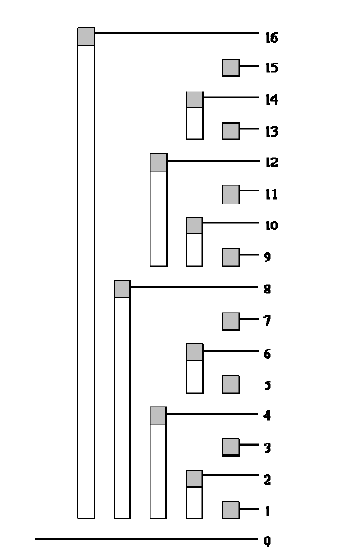
某些简单的单点修改操作,比如下面给出的题目,时间复杂度为 (O(log{n})) 。
某些简单的区间查询操作,比如下面给出的题目,时间复杂度为 (O(log{n})) 。
树状数组 1 :单点修改,区间查询 ( LuoguP3374 / LibreOJ#130 )
Description
已知一个数列,你需要进行下面两种操作:
- 将某一个数加上 (x);
- 求出某区间每一个数的和。
Solution
思考一下怎么用上面那种数据结构实现?
比较像线段树。
就是:
线段树的右儿子都被合并到父亲身上了。
对没错,所以树状数组完全是前缀和机器。
既然是前缀和,右儿子其实是没有必要的。
去掉右儿子的线段树,结点个数也就是 (n) 了。
ʌ 结构就变成了 」 结构
那么
(;)ʌ
ʌ ʌ
ʌ ʌ ʌ ʌ
就变成了
」
」 」
」」」」
跟二进制明显很有关系。(如果多写几个会更明显)
不妨从左到右标号为 1,2,3,4 用二进制表示
0 0 0 1
0 1 1 0
1 0 1 0
在原线段树中所在层数 = 二进制最低位 1 的位置
层数不妨从下往上标为 0 1 2 3
那么从左儿子跳到右儿子只需要加上 1 << 层数,这就是 Modify
幸运的左儿子可能跳一下跳到了一连串右儿子上就顺着飞升成为爸爸
至于求前缀和,就是作为一个左儿子要找它左边的左儿子
同样,减掉 1 << 层数 即可。
比如说 7 → 6 → 4 这样。放在线段树上查询区间和模拟一下就懂了。
这个 1 << 层数,实际上代表的是区间长度。
我仍旧建议放到线段树上思考。
而 lowbit(x) = x&((~x)+1) = x&-x
具体的与补码有关。
Code
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<cmath>
using namespace std;
const int MAXN = 1e6 + 10;
int n, m;
int a[MAXN];
long long BIt_Sum[MAXN];
#define lowbit(i) ((i)&-(i))
void BIt_Add(int Pos, int Val)
{
while (Pos <= n)
{
BIt_Sum[Pos] += Val;
Pos += lowbit(Pos);
}
}
long long BIt_Query(int Pos)
{
static long long Ans;
Ans = 0;
while (Pos)
{
Ans += BIt_Sum[Pos];
Pos -= lowbit(Pos);
}
return Ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
BIt_Add(i, a[i]);
}
for (int Opt, x, y, i = 1; i <= m; ++i)
{
cin >> Opt >> x >> y;
if (Opt==1)
{
BIt_Add(x, y);
continue;
}
cout << BIt_Query(y) - BIt_Query(x-1) << endl;
// Opt==2
}
return 0;
}
树状数组 2 :区间修改,单点查询 ( LuoguP3368 / LibreOJ#131 )
Description
已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 (x);
- 求出某一个数的值。
Solution
差分,区间加变成单点修改
同时单点查询变成前缀和,正好可以用树状数组。
Code
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<cmath>
using namespace std;
const int MAXN = 1e6 + 10;
int n, m;
int o[MAXN];
long long BIt_Sum[MAXN];
#define lowbit(i) ((i)&-(i))
void BIt_Add(int Pos, int Val)
{
while (Pos <= n)
{
BIt_Sum[Pos] += Val;
Pos += lowbit(Pos);
}
}
long long BIt_Query(int Pos)
{
static long long Ans;
Ans = 0;
while (Pos)
{
Ans += BIt_Sum[Pos];
Pos -= lowbit(Pos);
}
return Ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
o[0] = 0;
for (int i = 1; i <= n; ++i)
{
cin >> o[i];
BIt_Add(i, o[i] - o[i-1]);
}
for (int Opt, l, r, x, i = 1; i <= m; ++i)
{
cin >> Opt;
if (Opt==1)
{
cin >> l >> r >> x;
BIt_Add(l, x);
if (r<n) BIt_Add(r + 1, -x);
continue;
}
cin >> x;
cout << BIt_Query(x) << endl;
// Opt==2
}
return 0;
}
「SDOI2009」HH的项链 ( LuoguP1972 )
Description
已知一条项链穿了 (nlog n) 可过个数的贝壳,要求支持区间查询贝壳种数。
不强制在线。
Solution
莫队经典题。也可以分块。
你可能奇怪,这怎么树状数组?
离线,从左往右扫描的同时处理询问。如果现在扫描到 (i) ,就只处理右端点坐标为 (i) 的询问。
不妨把现在扫描到 (i) 看作 现在是第 (i) 秒,当前处理的所有询问就都变成:
从 (i-x) 秒到 (i) 秒这段时间内捡到了几种贝壳?
那么,每种贝壳只需要记录最后一次捡到的时刻即可。
最后一次捡到某个贝壳,往前的询问相当于往左伸手,必定先碰到这一次才能碰到更早的某一次。
那么除了最后一次捡到的时刻之外都是对答案没有贡献的。
然后标记每个时刻是否有最后一次捡到某种贝壳,统计答案的时候就统计查询的区间里面 true 的个数。
这就可以前缀和了。
实现上是:从左往右扫描
这个时刻捡到了一块贝壳就给这个时刻标记上1,然后把这个贝壳上次出现的时刻标记成0
(假如每个时刻可以有多块贝壳就要变成 ++ 和 -- ,但是那样的话这条项链有点奇葩)
同时维护这个01序列的前缀和。答案就是 Sum[i] - Sum[Left-1]
Code
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<cmath>
using namespace std;
const int MAXN = 1e6 + 10;
int N, M, Ai[MAXN] = {};
int LatestVis[MAXN] = {};
int BItree[MAXN] = {};
int FinalAns[MAXN] = {};
struct Query
{
int L, R, Id;
Query()
{
L = 0;
R = 0;
Id = 0;
}
} q[MAXN];
bool cmp(Query a, Query b)
{
if (a.R == b.R) return a.L < b.L;
return a.R < b.R;
}
#define lowbit(i) ((i)&-(i))
void BItAdd(int Pos, int Val)
{
while (Pos <= N)
{
BItree[Pos] += Val;
Pos += lowbit(Pos);
}
}
int BItQsum(int Pos)
{
static int Ans;
Ans = 0;
while (Pos)
{
Ans += BItree[Pos];
Pos -= lowbit(Pos);
}
return Ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> N;
for (int i = 1; i <= N; ++i)
{
cin >> Ai[i];
}
cin >> M;
for (int i = 1; i <= M; ++i)
{
cin >> q[i].L >> q[i].R;
q[i].Id = i;
}
sort(q + 1, q + 1 + M, cmp);
for (int qid = 1, i = 1; i <= N; ++i)
{
if (LatestVis[Ai[i]]) BItAdd(LatestVis[Ai[i]], -1);
BItAdd(i, 1);
LatestVis[Ai[i]] = i;
while (q[qid].R == i)
{
FinalAns[q[qid].Id] = BItQsum(q[qid].R) - BItQsum(q[qid].L - 1);
++qid;
}
}
for (int i = 1; i <= M; ++i) cout << FinalAns[i] << endl;
return 0;
}
树状数组 3 :区间修改,区间查询 ( LibreOJ#132 )
Solution
维护两个树状数组不就完了? ← 显然错误的想法
思考一下。修改还是得变成单点,所以要差分。 记差分数列 ({D_n})
前缀和是
也就是
分别维护两种前缀和。
Code
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<cmath>
using namespace std;
#define upre(nam, i, j) for (int nam = (i); nam <= (j); ++nam)
const int mx = 1e6 + 10;
int N, Q;
int a[mx]={};
long long BIT[mx]={};
long long iBIT[mx]={};
#define lb(i) ((i)&-(i))
void Bad(int p, int x)
{
static int pp;
pp = p;
while (p <= N)
{
iBIT[p]+=1ll * (pp-1) * x;
BIT[p]+=x;
p += lb(p);
}
}
long long Ban(int p, bool isi)
{
static long long Ans;
Ans = 0;
while (p)
{
isi ? Ans += iBIT[p] : Ans += BIT[p];
p -= lb(p);
}
return Ans;
}
long long Qer(int l, int r)
{
return Ban(r,0)*r-Ban(r,1)-Ban(l-1,0)*(l-1)+Ban(l-1,1);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> N >> Q;
upre(i, 1, N)
{
cin >> a[i];
Bad(i, a[i]-a[i-1]);
}
int meme, l, r, x;
upre(i, 1, Q)
{
cin >> meme >> l >> r;
if (meme==2)
{
cout << Qer(l, r)<<endl;
continue;
}
cin >> x;
Bad(l, x);
Bad(r+1, -x);
}
return 0;
}
I Hate It ( Luogu1531 )
按照最开始讲的那样。
发现树状数组其实跟线段树一样,可以做到支持区间操作(而不是前/后缀和相减)
也就是说可以支持区间最值
不过比起支持前/后缀和麻烦很多。
而且树状数组支持区间最值是通过有点二进制的方式,所以单次查询复杂度会是 (O(log^2n))