一、非线性结构:图
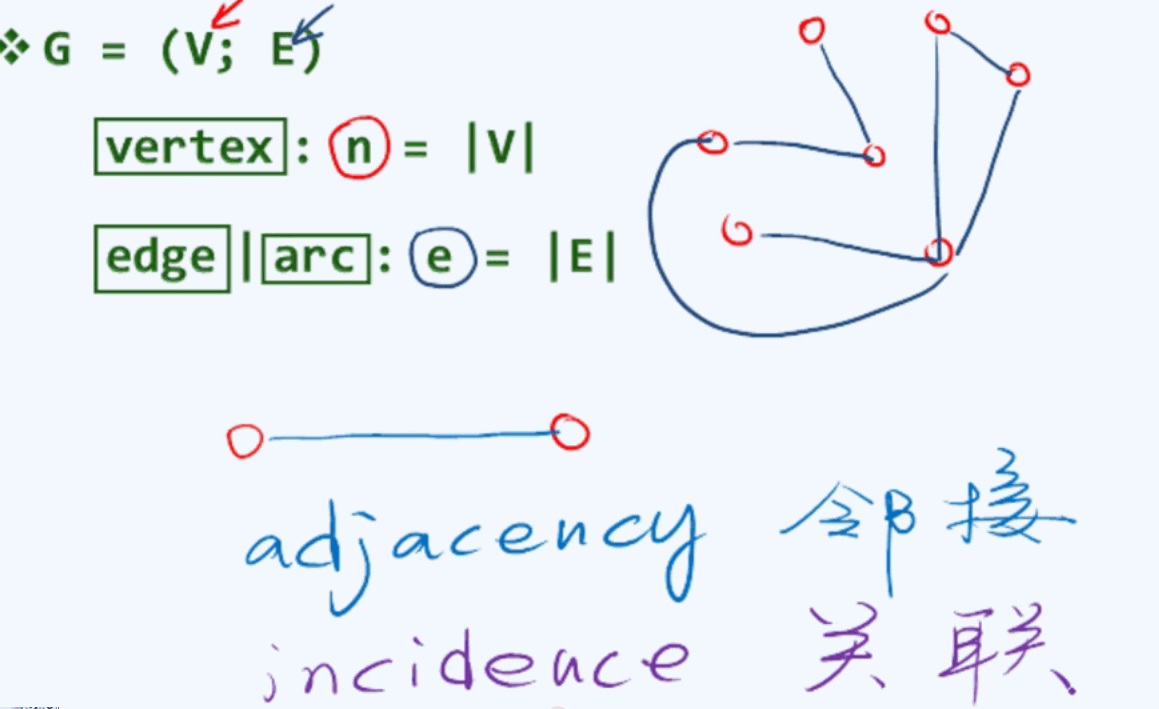
图由顶点集V,集合规模为n,在n个顶点之间可能存在对应关系,我们用连边来描述这种,即边E,规模为e。
邻接关系:顶点与顶点之间的关系;关联关系:顶点与它相连的边的关系。序列结构(vector和list)是图的一种特例,只有相邻点之间才可以定义临接关系,而树结构只有父节点和子节点之间构成临接关系,也是图的一种特例,而图任意两个节点之间都可以构成临接关系。
二、有向图和无向图
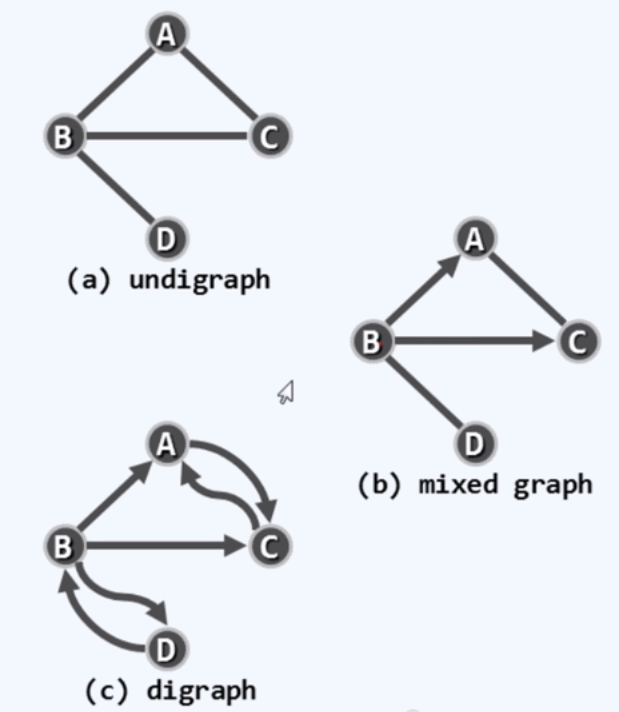
若邻接顶点u和v的次序无所谓,则(u,v)是无向边(undirected edge).所有边均为无方向的图,称为无向图。(undigraph).反之,有向图(digraph)中均为有向边(directed edge),u,v分别称作边(u,v)的head和tail.
我们主要研究有向图,有向图可以用来描述其他图。
三、通径和环路
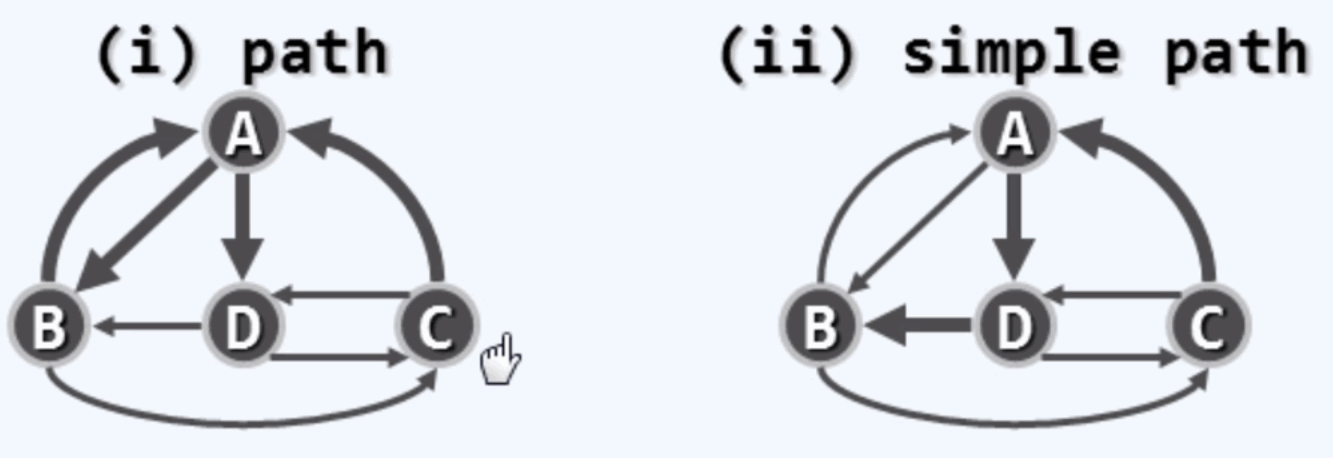
路径:由系列顶点按照依次邻接关系构成的序列。
简单路径(simple cycle):其中不含重复节点的路径 .不简单路径(unsimple cycle):含有重复节点的路径
环路:v0 = vk :路径的起点和终点是重合的
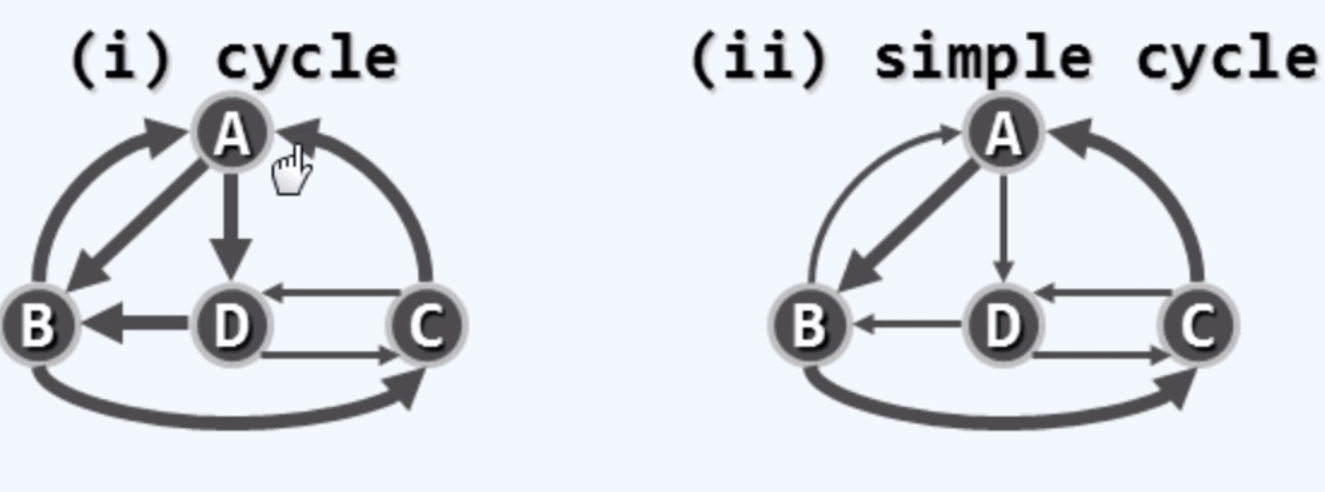
欧拉环路: 覆盖了图中所有的边。
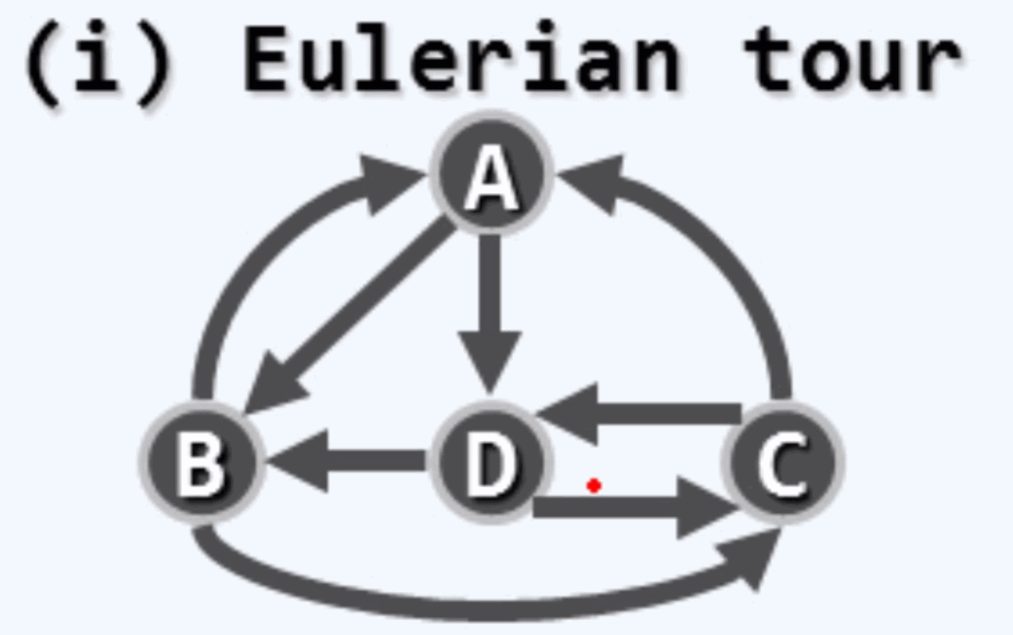
哈密尔顿环路:

四、图的接口
Graph模板类:
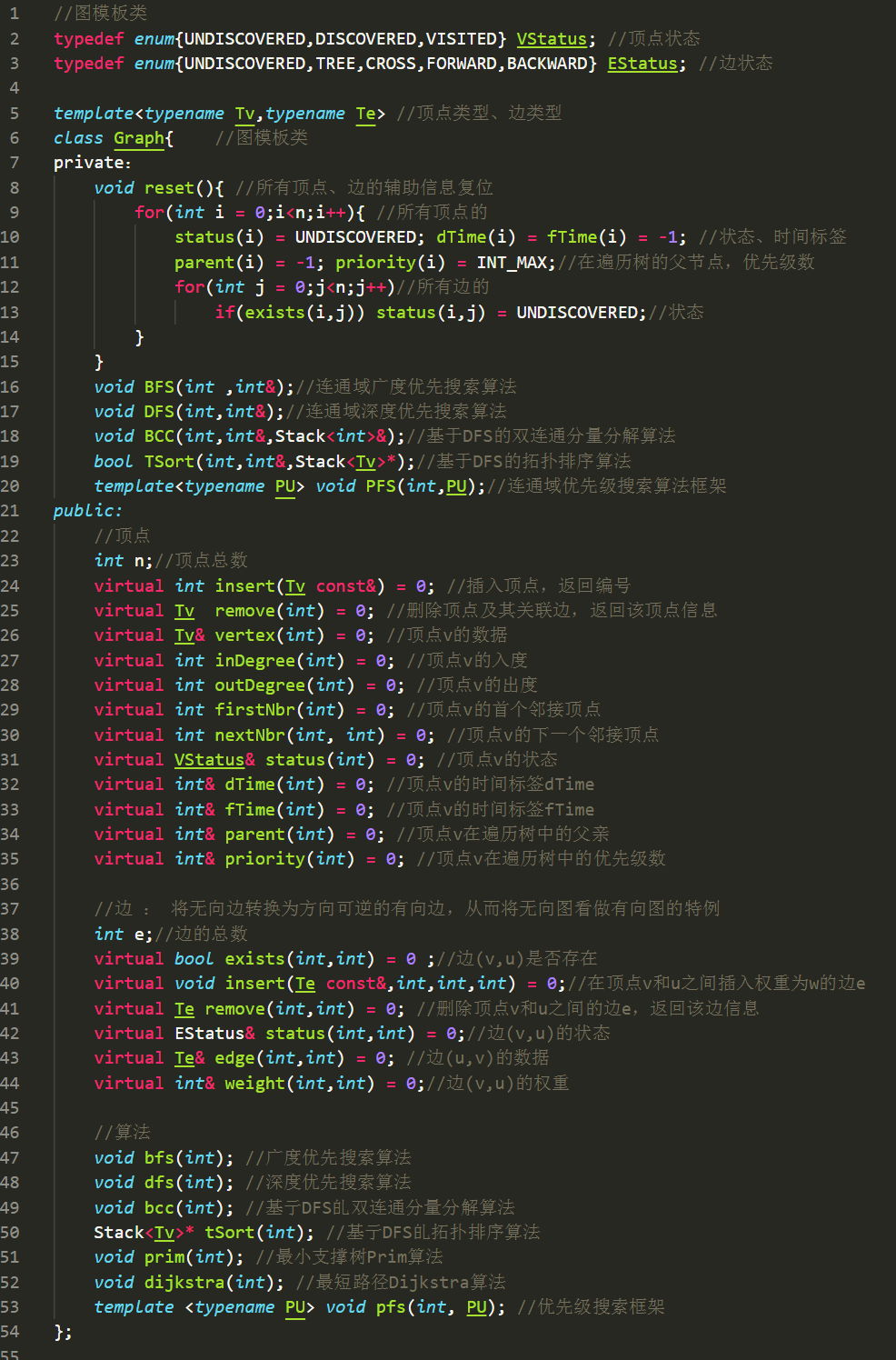
邻接矩阵和关联矩阵:
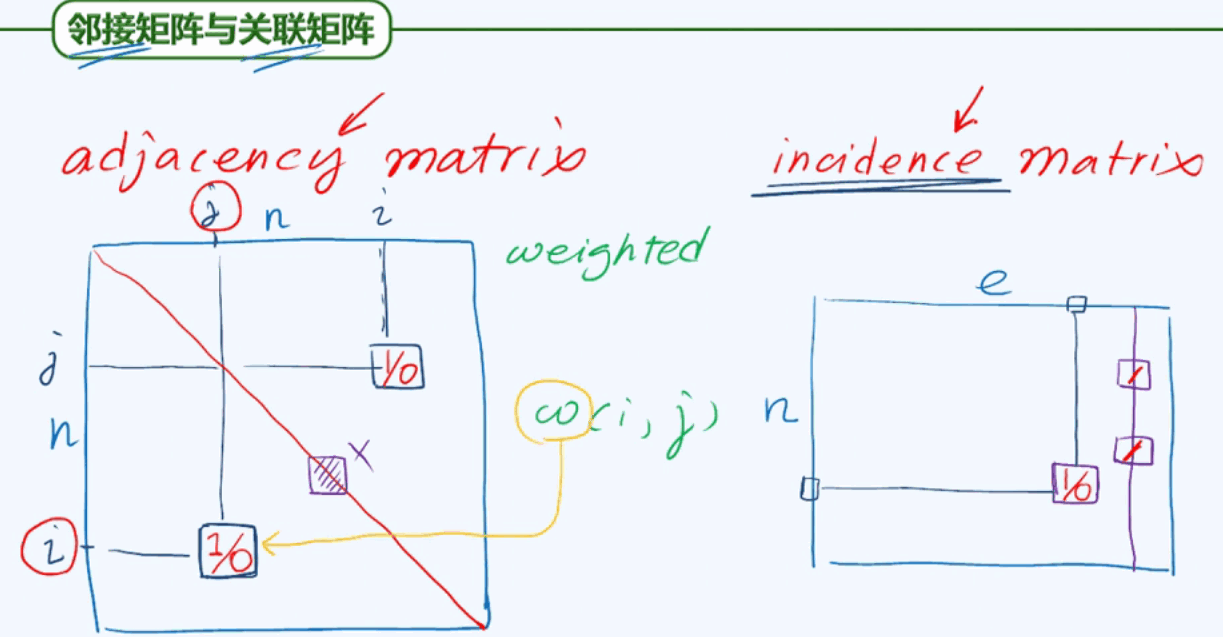
无向图的邻接矩阵存在一定冗余性,它在邻接矩阵中的值保存了两次。
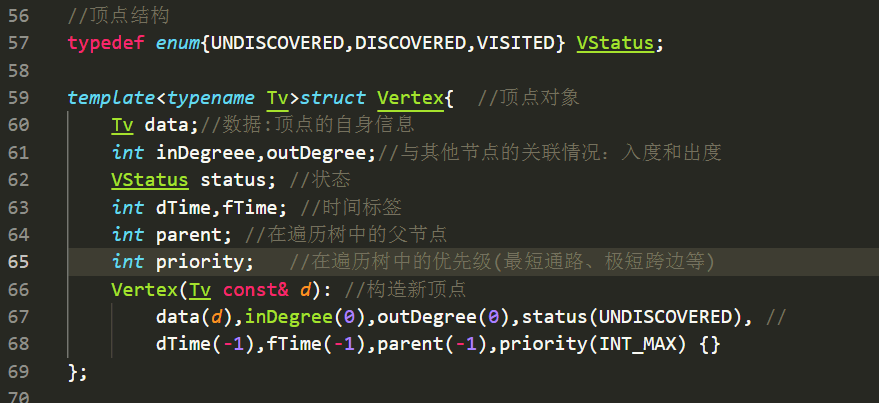
顶点结构:
边结构:

GraphMatrix: E是一个二维向量。

顶点的基本操作:

任意顶点i枚举其所有的邻接顶点: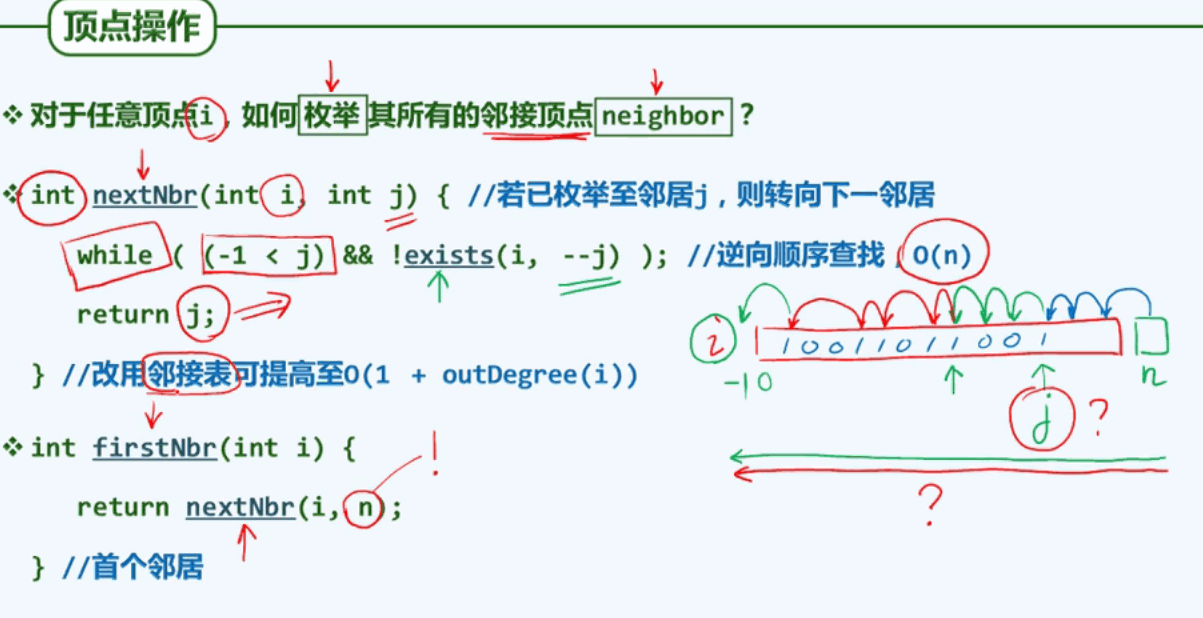
顶点的插入和删除,会改变邻接矩阵的规模,而边并不会。


边操作:
判断某条边是否存在?
返回边的其他信息:

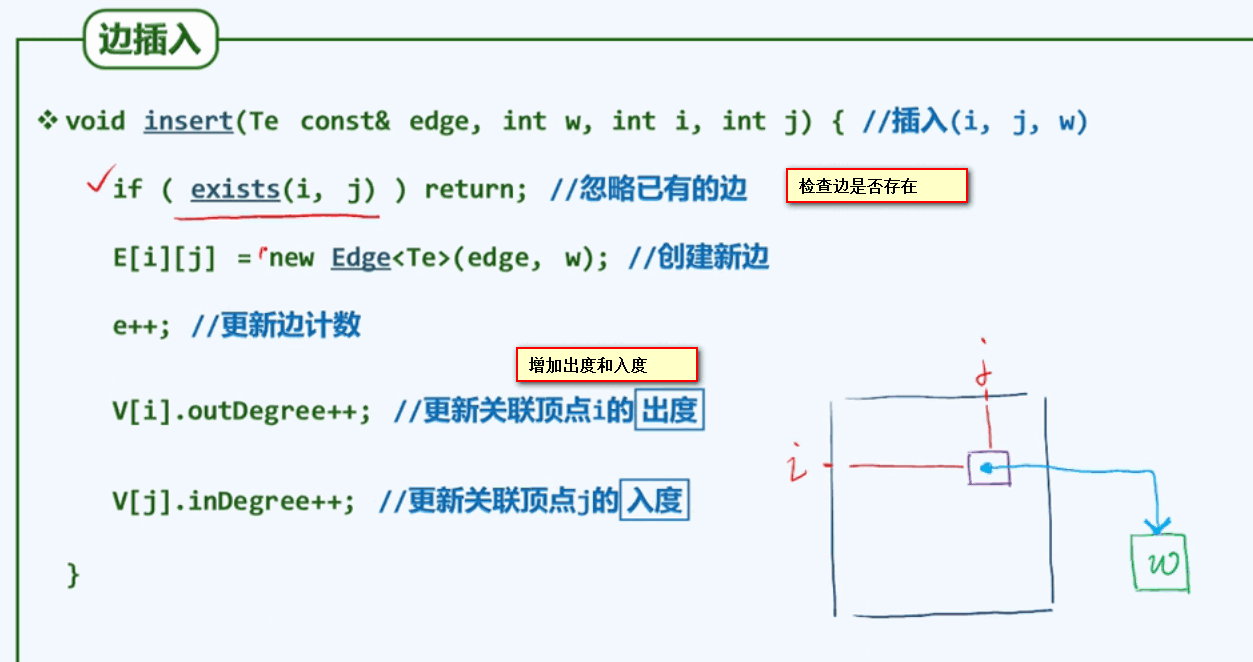
插入一条新的边:
删除一条已经存在的边:

总结:邻接矩阵表示法:

缺点:
平面图:不存在相交的边。

图的相关算法:将图转换为树
广度优先搜索:不折不扣的层次遍历,图 的广度优先遍历就等同于树的层次遍历: 每个顶点与s之间的那条通路,恰好就是在原图中这两个顶点之间的那条最短通路。
· 
BFS只是一个算法框架,

对于邻居顶点的不同处理方法如下所示:

BFS的实例:得到一颗遍历支撑树,其实也很简单。
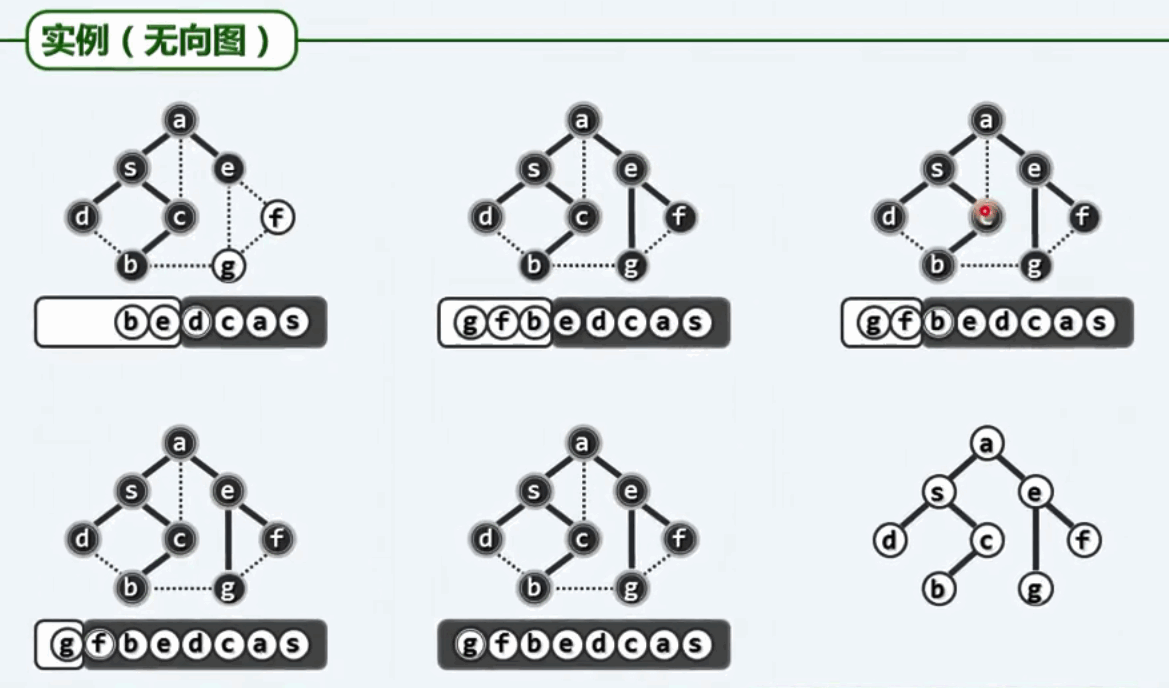
如何使BFS覆盖整幅图,而不是其中的某一个顶点呢?

存储级别之间的巨大的速度差异,在实际应用中往往更为举足轻重:因此如此实现的BFS算法的实际性能时n+e:至少对每个顶点和每条边访问一次。
作为后续算法的一个基本框架,已经达到了一个比较低廉的成本:对于使用邻接表实现的BFS,其时间复杂度就是O(n+e)
深度优先搜索(DFS):深度优先搜索是一个不断回溯的过程。类似于树的先序遍历:

DFS的基本框架:
内部实现算法:
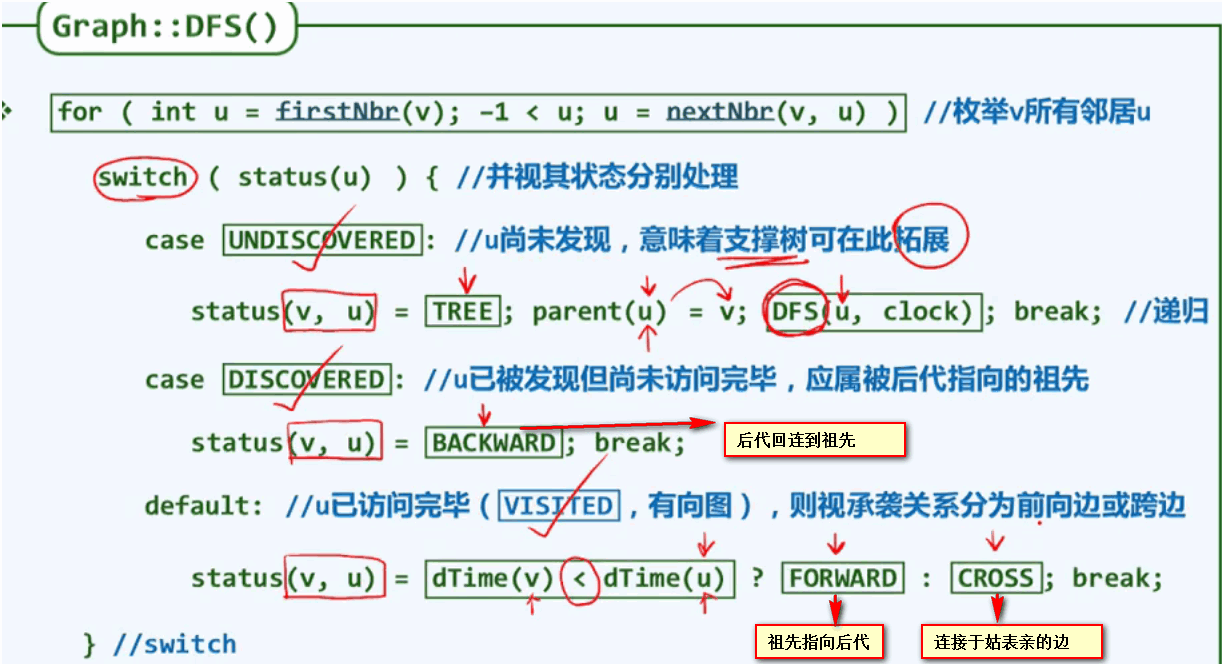
实例:

DFS的有向图实例:
出现一条BACKWARD就说明发现了一条回路。
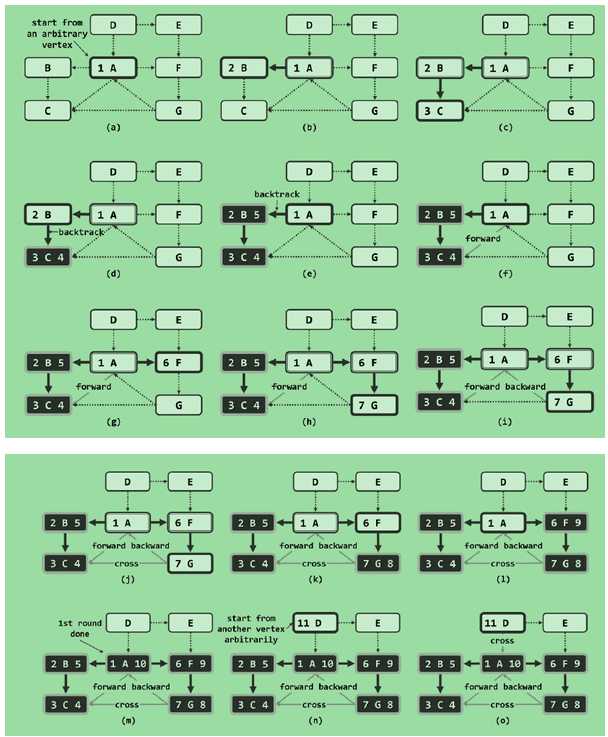
在遍历的最外层包装一层循环,以保证DFS遍历所有的顶点:
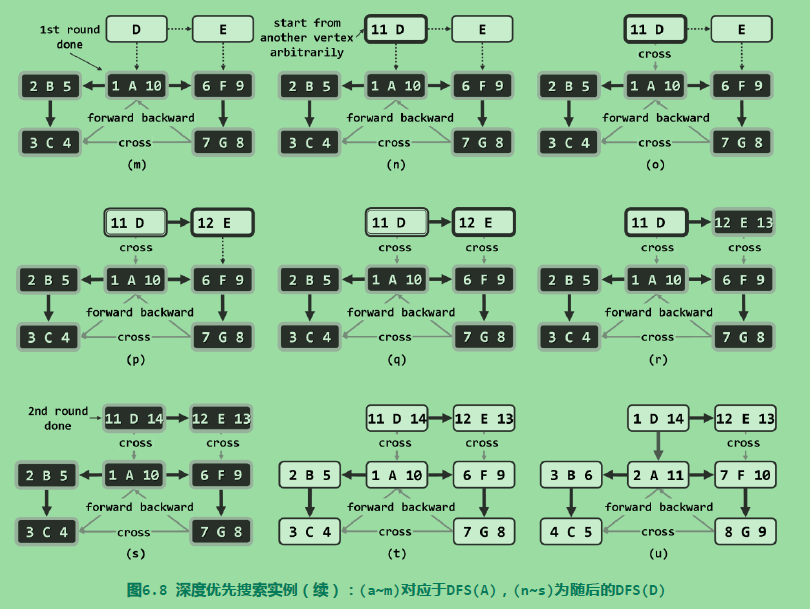
借助时间标签可以快速的判断两个节点之间在整个遍历树中是否存在直系血缘关系:
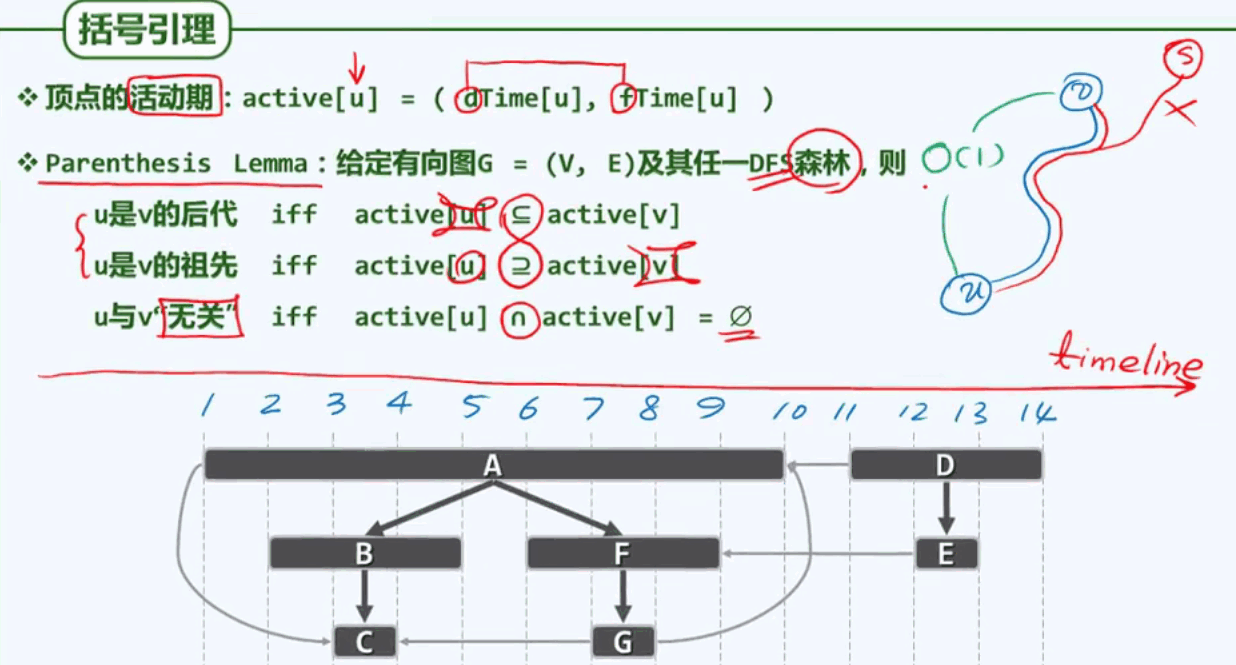
拓扑排序
每一顶点都不会通过边,指向其在此序列中的前驱顶点,这样的一个线性序列,称作原有向图的一个拓扑排序(topological sorting)。
给定一个描述实际应用的有向图,如何在于该图相容的前提下,将所有顶点排成一个线性序列。
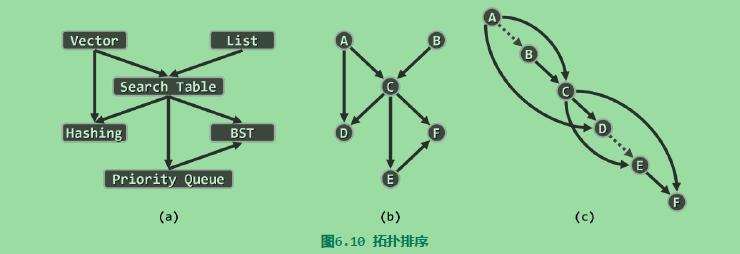
有向无环图必然存在拓扑排序,拓扑排序存在,那么它必定是一个有向无环图。有向无换图属于偏序关系,而拓扑排序则对应于全序关系,在顶点数目有限时,与任一偏序相容的全序必然存在。
任一有限偏序集,必有极值元素,类似,任一有向无环图,也必然包含入度为0的顶点。
于是只要将入度为0的顶点m(及其关联边)从图G中取出,则剩余的G‘依然是有向无环图,故其拓扑排序依然存在。从递归的角度看,一旦得到了G’的拓扑排序,只需要将m作为最大顶点插入即可,即可得到G的拓扑排序,如此我们得到了一个拓扑排序的算法。

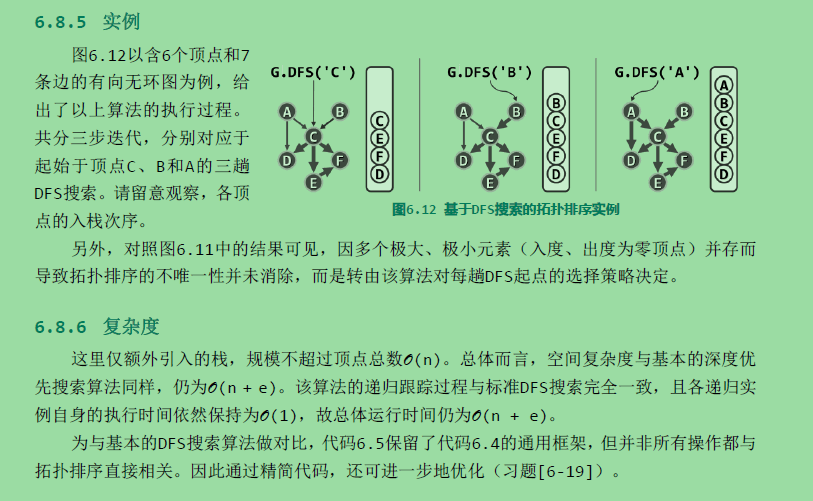
将关注点,转到与极大顶点相对称的极小顶点。DFS搜索过程中各顶点被标记为VISITED的次序,恰好(按逆序)给出了原图的一个拓扑排序。具体地,搜索过程中一旦发现后向边,即可终止算法并报告“因非DAG而无法拓扑排序”。
实现:

实例如下:
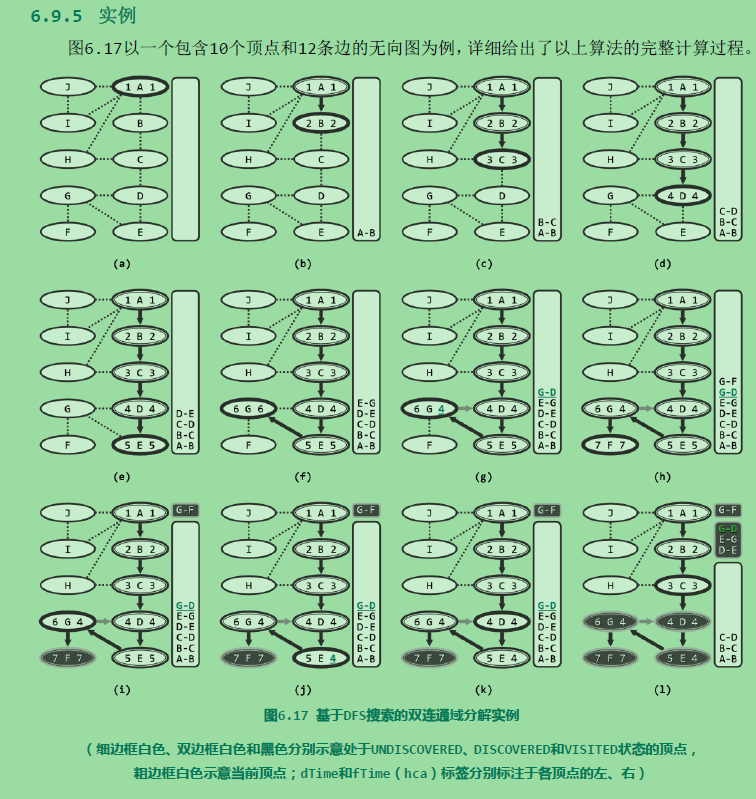
双连通域分解:
考查无向图G。若删除顶点v后G所包含的连通域增多,则v称作切割节点(cut vertex)或关节点(articulation point)。如图6.13中的C即是一个关节点——它的删除将导致连通域增加两块。反之,不含任何关节点的图称作双连通图。任一无向图都可视作由若干个极大的双连通子图组合而成,这样的每一子图都称作原图的一个双连通域(bi-connected component)。例如图6.14(a)中的无向图,可分解为如图(b)所示的三个双连通域。

较之其它顶点,关节点更为重要。在网络系统中它们对应于网关,决定子网之间能否连通。在航空系统中,某些机场的损坏,将同时切断其它机场之间的交通。故在资源总量有限的前提下,找出关节点并重点予以保障,是提高系统整体稳定性和鲁棒性的基本策略。题目中的bus station也是一个关节点。
如何找出关节点?
蛮力算法
由其定义,可直接导出蛮力算法大致如下:首先,通过BFS或DFS搜索统计出图G所含连通域的数目;然后逐一枚举每个顶点v,暂时将其从图G中删去,并再次通过搜索统计出图G{v}所含连通域的数目。当且仅当图G{v}包含的连通域多于图G时,节点v就是关节点。这一算法需执行n趟搜索,耗时O(n(n + e)),如此低的效率无法令人满意。
可行算法
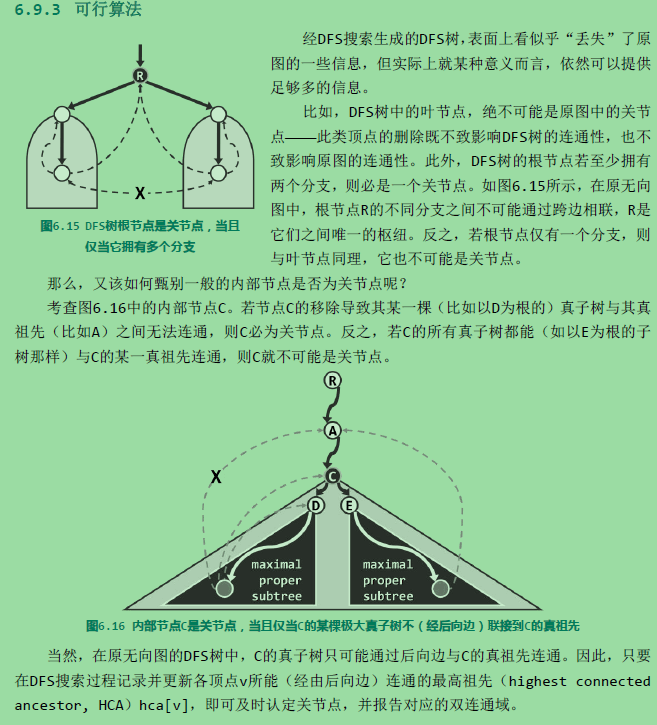
算法:

由于处理的是无向图,故DFS搜索在顶点v的孩子u处返回之后,通过比较hca[u]与dTime[v]的大小,即可判断v是否关节点。这里将闲置的fTime[]用作hca[]。故若hca[u] 大于等于 dTime[v],则说明u及其后代无法通过后向边与v的真祖先连通,故v为关节点。既然栈S存有搜索过的顶点,与该关节点相对应的双连通域内的顶点,此时都应集中存放于S顶部,故可依次弹出这些顶点。v本身必然最后弹出,作为多个连通域的联接枢纽,它应重新进栈。反之若hca[u] < dTime[v],则意味着u可经由后向边连通至v的真祖先。果真如此,则这一性质对v同样适用,故有必要将hca[v],更新为hca[v]与hca[u]之间的更小者。当然,每遇到一条后向边(v, u),也需要及时地将hca[v],更新为hca[v]与dTime[u]之间的更小者,以保证hca[v]能够始终记录顶点v可经由后向边向上连通的最高祖先。

复杂度
与基本的DFS搜索算法相比,这里只增加了一个规模O(n)的辅助栈,故整体空间复杂度仍为O(n + e)。时间方面,尽管同一顶点v可能多次入栈,但每一次重复入栈都对应于某一新发现的双连通域,与之对应地必有至少另一顶点出栈且不再入栈。因此,这类重复入栈操作不会超过n次,入栈操作累计不超过2n次,故算法的整体运行时间依然是O(n + e)。
优先级搜索
每一种选取策略都等效于,给所有顶点赋予不同的优先级,而且随着算法的推进不断调整;而每一步迭代所选取的顶点,都是当时的优先级最高者。按照这种理解,包括BFS和DFS在内的几乎所有图搜索,都可纳入统一的框架。鉴于优先级在其中所扮演的关键角色,故亦称作优先级搜索(priority-first search, PFS),或最佳优先搜索(best-first search, BFS)。为落实以上理解,图ADT(表6.2和代码6.1)提供了priority()接口,以支持对顶点优先级数(priority number)的读取和修改。在实际应用中,引导优化方向的指标往往对应于某种有限的资源或成本(如光纤长度、通讯带宽等),故不妨约定优先级数越大(小)顶点的优先级越低(高)。相应地,在算法的初始化阶段(如代码6.1中的reset()),通常都将顶点的优先级数统一置为最大(比如INT_MAX)——或等价地,优先级最低。

可见,PFS搜索的基本过程和功能与常规的图搜索算法一样,也是以迭代方式逐步引入顶点和边,最终构造出一棵遍历树(或者遍历森林)。如上所述,每次都是引入当前优先级最高(优先级数最小)的顶点s,然后按照不同的策略更新其邻接顶点的优先级数。这里借助函数对象prioUpdater,使算法设计者得以根据不同的问题需求,简明地描述和实现对应的更新策略。具体地,只需重新定义prioUpdater对象即可,而不必重复实现公共部分。比如,此前的BFS搜索和DFS搜索都可按照此模式统一实现。
PFS搜索由两重循环构成,其中内层循环又含并列的两个循环。若采用邻接表实现方式,同时假定prioUpdater()只需常数时间,则前一内循环的累计时间应取决于所有顶点的出度总和,即O(e);后一内循环固定迭代n次,累计O(n2)时间。两项合计总体复杂度为O(n2)。
最小支撑树
连通图G的某一无环连通子图T若覆盖G中所有的顶点,则称作G的一棵支撑树或生成树(spanning tree)。

就保留原图中边的数目而言,支撑树既是“禁止环路”前提下的极大子图,也是“保持连通”前提下的最小子图。在实际应用中,原图往往对应于由一组可能相互联接(边)的成员(顶点)构成的系统,而支撑树则对应于该系统最经济的联接方案。确切地,尽管同一幅图可能有多棵支撑树,但由于其中的顶点总数均为n,故其采用的边数也均为n - 1。
prim算法步骤:
- 以某一个点开始,寻找当前该点可以访问的所有的边;
- 在已经寻找的边中发现最小边,这个边必须有一个点还没有访问过,将还没有访问过的点加入我们的集合,记录添加的边;
- 寻找当前集合可以访问的所有边,重复2的过程,直到没有新的点可以加入。
- 此时由所有边构成的树即为最小生成树。
最短路径树: