【字符串】基于确定状态自动机(dfa)的kmp算法（算法第四版）

一、确定状态自动机（dfa）解释

有限状态的集合，还包含了从一个状态到另外一个状态的转换。有穷自动机看上去就像是一个有向图，其中状态是图的节点，而状态转换则是图的边。此外这些状态中还必须有一个初始状态和至少一个接受状态。状态转移的性质又分为确定的自动机（DFA）和非确定的自动机（NFA）。

二、dfa自己的理解

如果做过Leetcode动态规划相关题目的话，理解就比较容易了。

lc上的买卖股票问题就是很经典的动态规划问题。

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/

三、算法第四版dfa演化

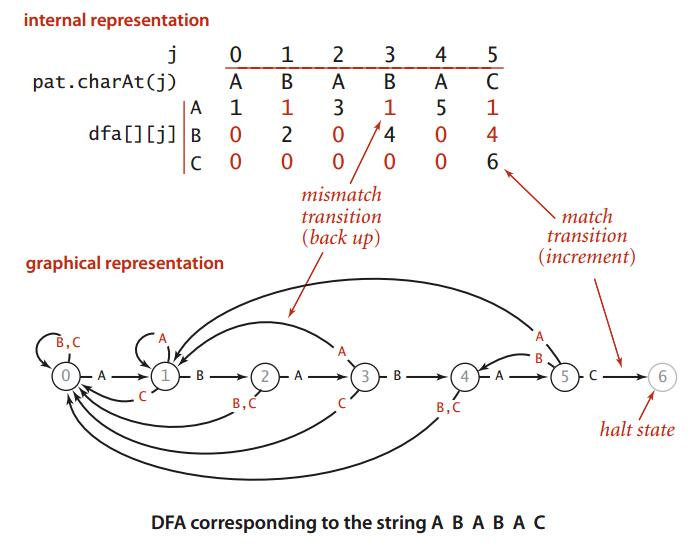
第一步：

因为A匹配所以若果是A就可以到状态1，B,C就还是状态0。那么结果就是1 0 0；

第二步：

因为就两个字母A和B,中间没有了，所以就复制j=0时的状态为 1 0 0，然后又因为B是匹配的可以进入到下一个状态，所以就把B的那一个更新为2，结果就是 1 2 0

第三步：

因为有三个字母了，就把第1个字母B和第0个字母匹配，因为第0个字母是A，匹配失败，所以还是把j=0的状态复制过来得到 1 0 0,  然后又因为A是匹配的可以进入到下一个状态，所以就把A的那一个更新为3，结果就是 3 0 0

第四步：

现在就是有四个字母了，就把中间的B,A和第0个字母进行比较，先用B和第0个字母比较，因为第0个字母是A，所以失败。再用A和第0个字母比较，显然比较成功，那么就进入状态1，因为状态是从0开始的，现在就把j=1的值复制过来得到1  2  0，然后又因为B是匹配的可以进入到下一个状态，所以就把B的那一个更新为4，结果就是 1  4  0

第五步：

现在有5个字母了，就把中间的B,A,B和第0个字母进行比较，先用B和第0个字母比较，因为第0个字母是A，所以失败。再用A和第0个字母比较，显然比较成功。继续用B和第1个字母比较，因为第1个字母是B，比较成功，所以就把j=2的状态复制过来得到3  0  0，然后又因为A是匹配的可以进入到下一个状态，所以就把A的那一个更新为5，结果就是 5  0  0

第六步：

现在有6个字母了，就把中间的B,A,B,A和第0个字母进行比较，先用B和第0个字母比较，因为第0个字母是A，所以失败。再用A和第0个字母比较，显然比较成功。继续用B和第1个字母比较，因为第1个字母是B，比较成功。继续用A和第2个字母比较，因为第2个字母是A，比较成功，所以就把j=3的状态复制过来得到1  4  0，然后又因为C是匹配的可以进入到下一个状态，所以就把C的那一个更新为6，结果就是 1  4  6

public kmp(String pat)
    {
        this.pat=pat;
        int M=pat.length();
        int R=256;
        dfa=new int[R][M];
        dfa[pat.charAt(0)][0]=1;
//构造dfa数组
        for(int X=0,j=1;j<M;j++)
        {
            for(int c=0;c<256;c++)
                dfa[c][j]=dfa[c][X];
            dfa[pat.charAt(j)][j]=j+1;
            X=dfa[pat.charAt(j)][X];
        }
    }

四、kmp完整代码

public class kmp {
    private String pat;
    private int[][] dfa;
    public kmp(String pat)
    {
        this.pat=pat;
        int M=pat.length();
        int R=256;
        dfa=new int[R][M];
        dfa[pat.charAt(0)][0]=1;
        for(int X=0,j=1;j<M;j++)
        {
            for(int c=0;c<256;c++)
                dfa[c][j]=dfa[c][X];
            dfa[pat.charAt(j)][j]=j+1;
            X=dfa[pat.charAt(j)][X];
        }
    }
    public int search(String txt)
    {
        int i,j,N=txt.length(),M=pat.length();
        for(i=0,j=0;i<N&&j<M;i++)
        {
            j=dfa[txt.charAt(i)][j];
        }
        if(j==M) return i-M;
        else return N;
    }

    public static void main(String[] args) {
        String pat=args[0];
        String txt=args[1];
        kmp k=new kmp(pat);
        //以下输出的语句和空格的输出是为了结果模式串和主串匹配的地方一一匹配
        System.out.println("text:   "+txt);
        int offset= k.search(txt);
       // System.out.print("
");
        System.out.print("pattern:");
        for(int i=0;i<offset;i++)
        {
            System.out.print(" ");
        }
        System.out.print(pat);

    }
}

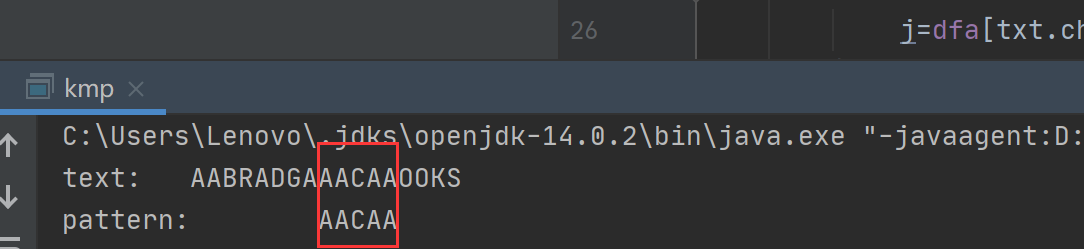
 五、kmp题目变体(TODO:代码要改！！！)

我曾经记得在大一上学习c语言课程设计的时候 做过kmp的题

大概题目是这样的：

给你一个模式串和主串，利用kmp算法（不能暴力），要求求出主串中可以匹配多少个模式串

AACABACABAACACA          ACA    输出 4

  1        1           1   1

上面的kmp算法如果有匹配到就直接返回了 不会判断主串剩余的是否还有

public class kmp {
    private String pat;
    private int[][] dfa;
    public kmp(String pat)
    {
        this.pat=pat;
        int M=pat.length();
        int R=256;
        dfa=new int[R][M];
        dfa[pat.charAt(0)][0]=1;
        for(int X=0,j=1;j<M;j++)
        {
            for(int c=0;c<256;c++)
                dfa[c][j]=dfa[c][X];
            dfa[pat.charAt(j)][j]=j+1;
            X=dfa[pat.charAt(j)][X];
        }
    }
    public int search(String txt)
    {
        int i,j,N=txt.length(),M=pat.length();
        int count=0;
        for(i=0,j=0;i<N;i++)
        {
            j=dfa[txt.charAt(i)][j];
            if(j==M){
                count++;
                j=0;
            }

        }
//        if(j==M) return i-M;
//        else return N;
        return count;
    }

    public static void main(String[] args) {
        String pat=args[0];
        String txt=args[1];
        kmp k=new kmp(pat);
        int n=k.search(txt);
        System.out.println(n);
        //以下输出的语句和空格的输出是为了结果模式串和主串匹配的地方一一匹配
//        System.out.println("text:   "+txt);
//        int offset= k.search(txt);
//       // System.out.print("
");
//        System.out.print("pattern:");
//        for(int i=0;i<offset;i++)
//        {
//            System.out.print(" ");
//        }
//        System.out.print(pat);

    }
}