目录
EM算法(4):EM算法证明
1. 概述
上一篇博客我们已经讲过了EM算法,EM算法由于其普适性收到广泛关注,高频率地被运用在各种优化问题中。但是EM算法为什么用简单两步就能保证使得问题最优化呢?下面我们就给出证明。
2. 证明
现在我们已经对EM算法有所了解,知道其以两步(E-step和M-step)为周期,迭代进行,直到收敛为止。那问题就是,在一个周期内,目标函数的值是否增加了?如果能保证其每个周期都在增加的话,那么其必然收敛到一个局部最大值处。这就是我们EM算法所需要证明的,即:
$p(mathbf{X}; heta^{(i+1)}) geqslant p(mathbf{X}; heta^{(i)})$
首先假设Y的分布为$q(mathbf{Y})$,则有$sum_Yq(mathbf{Y}) = 1$,则:
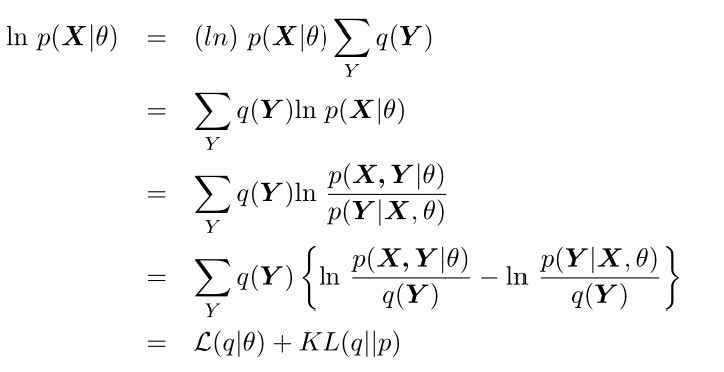
现在假设在EM算法第i个周期结束,因为KL(q||p)不小于零,那么其最小时就为0,即$q(mathbf{Y})=p(mathbf{Y}|mathbf{X}, heta^{(i)})$时。
在E-step时,我们计算$Q( heta^{(i+1)}| heta^{(i)})$,我们发现:

在M-step时,我们找到一个$ heta^{(i+1)}$,使得$Q( heta| heta^{(i)})$最大,即也是使得$mathcal{L}(q| heta)$最大。同时,因为此时$p(mathbf{X,Y}| heta^{(i+1)}) eq p(mathbf{X,Y}| heta^{(i)}) = q(mathbf{Y})$,那么KL(q||p)也会大于零。那么相对于第i个EM周期结束时的目标函数的值,现在其两个和项的值都是非减的,那么很容易得到:
$p(mathbf(X)| heta^{(i+1)}) geqslant p(mathbf{X}| heta^{(i)})$