目录
EM算法(2):GMM训练算法
1. 简介
GMM模型全称为Gaussian Mixture Model,即高斯混合模型。其主要是针对普通的单个高斯模型提出来的。我们知道,普通高斯模型对实际数据拟合效果还不错,但是其有一个致命的缺陷,就是其为单峰函数,如果数据的真实分布为复杂的多峰分布,那么单峰高斯的拟合效果就不够好了。
与单峰高斯模型不同,GMM模型是多个高斯模型的加权和,具体一点就是:
$p(mathbf{x}) = sum_kpi_kmathcal{N}(mathbf{x}|mu_k,Sigma_k)$
这是一个多峰分布,理论上,只要k足够大,GMM模型能拟合任何分布。
2. 困难
GMM模型比普通高斯模型拟合能力更强了,但是对其训练的难度也增加了。回忆一下,在训练普通高斯模型时,我们是对其分布函数去ln进行求导,具体一点就是:
$frac{partial lnp(mathbf{x})}{partial mathbf{ heta}} = 0$
那么对于普通高斯函数来说,$lnp(mathbf{x}) = C - frac{1}{2}(mathbf{x}-mu)^TSigma^{-1}(mathbf{x}-mu)$,可以看到,ln将分布函数中的指数形式消除了,那么对其求导很容易得到闭式解。但是对于GMM模型来说就不是这么简单了。我们可以计算一下,其概率函数取ln形式为:
$lnp(mathbf{x}) = ln{ sum_kpi_kmathcal{N}(mathbf{x}|mu_k,Sigma_k)}$
我们可以看到,因为在ln里面还有加法,所以其无法消除其中的指数形式,导致其最优化问题没有闭式解。所以想要用calculus的方式来解决GMM模型训练的问题是不行的。
3. Inspiration from k-means algorithm
没有什么事情是一步解决不了的,如果有,那就用两步。
--沃 · 兹基硕德
我们重新来看看GMM模型的表达式,其由多个高斯函数相加而成,你可以想想一个空间中有很多高斯函数,它们分别在各自中心点所在的位置。一个一维的三个高斯混合的模型示意如下:
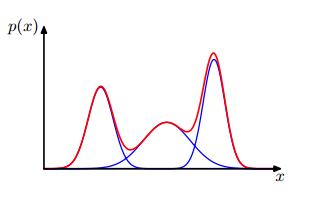
那么对于任何一个点,都有其最靠近的一个峰。比如在中间峰处的点,其概率几乎全是来自于第二个高斯分布。那么我们就可以这样想,是不是每个点都有其更加偏向的高斯峰呢?等等,这个想法好像在哪里见过?k-means算法中的第一步不就是干的这事吗?将每个点都分配给最近的一个类。但是,我们这里怎么去度量距离呢?继续使用点到中心的距离?这样好像把每个高斯的方差忽略掉了。那么既然是概率模型,最好的方法就是用概率来比较。对于一个点$mathbf{x}$,第k个高斯对其的贡献为$pi_kmathcal{N}(mathbf{x}|mu_k,Sigma_k)$,那么把$mathbf{x}$分配给贡献最大的一个,这样看起来把各个因素考虑进去,似乎很合理了。
但是,我们发现,如果一个点处于两个峰之间呢,这样把其归为任何一个峰都不太好吧?当然,k-means也没有解决这个问题,但是我们这里是概率模型,我们有更好的描述方法,我们可以计算一个点$mathbf{x}$属于每个高斯的概率。这样的考虑就比较全面了。那么点$mathbf{x}$属于每个高斯的概率自然就取这个高斯对其的贡献$pi_kmathcal{N}(mathbf{x}|mu_k,Sigma_k)$。为了使其成为一个概率,我们还需要对其归一化,所以得到第n个数据点属于第k个高斯的概率:
$gamma_{nk}=frac{pi_kmathcal{N}(mathbf{x}_n|mu_k,Sigma_k)}{sum_jpi_jmathcal{N}(mathbf{x}_n|mu_j,Sigma_j)}$
按照k-means算法,第二步就是把$gamma_{nk}$当做已知去做最优化。这里既然是要拟合分布,那么就使用最大似然的方法,最大化$lnp(mathbf{X})$。那么这里就有一个问题了:在k-means算法中,目标函数是有$r_{nk}$这一项的,然而$lnp(mathbf{X})$中并没有$gamma_{nk}$这一项呀,我怎么把其当做已知的呢?这里我们不急,暂时不去管这个,我们先计算$frac{partial lnp(mathbf{X})}{partial mu_k}$:
$frac{partial lnp(mathbf{X})}{partial mu_k} = - sum_nfrac{pi_kmathcal{N}(mathbf{x}_n|mu_k,Sigma_k)}{sum_jpi_jmathcal{N}(mathbf{x}_n|mu_j,Sigma_k)}Sigma_k(mathbf{x}_n - mu_k) $ (1)
我们的$gamma_{nk}$是不是已经出现了,那么上式可以简写为:
$ - sum_ngamma_{nk}Sigma_k(mathbf{x}_n - mu_k)$
令其等于0,可以得到:
$mu_k = frac{sum_ngamma_{nk}mathbf{x}_n}{sum_ngamma_{nk}}$ (2)
可以看到,其与k-means算法第二步中心点的计算方法$mu_k=frac{sum_nr_{nk}mathbf{x}_n}{sum_nr_{nk}}$非常相似。
类似的,对$Sigma_k$求导,可以得到:
$Sigma_k = frac{sum_ngamma_{nk}(mathbf{x}_n-mu_k)(mathbf{x}_n-mu_k)^T}{sum_ngamma_{nk}}$ (3)
对$pi_k$求导,可以得到:
$pi_k = frac{sum_ngamma_{nk}}{sum_ksum_ngamma_{nk}}$ (4)
自此,GMM训练方法就得到了,第一步,使用式(1)计算所有点的属于各个高斯的概率;第二步,利用式(2),(3),(4)更新均值、方差和权值。重复这两步直到收敛。
4. 与EM算法的关系
这里我们是从k-means算法出发得到的GMM训练算法,那么其与EM算法的关系与k-means算法和EM算法的关系类似。同样,我们后面可以看到,利用EM算法可以推导出GMM训练算法。