树的特点:



树的遍历:
广度优先遍历 一层一层的遍历(可以依靠Queue来实现)
深度优先遍历:
先序: 根 左 右
中序: 左 根 右
后序: 左 右 根
满二叉树和完全二叉树的区别:
完全二叉树是由满二叉树而引出来的。对于bai深度为duK的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
对于满二叉树,除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。而完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
1.满二叉树
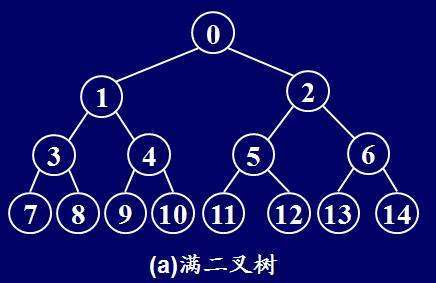
定义:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
2.完全二叉树
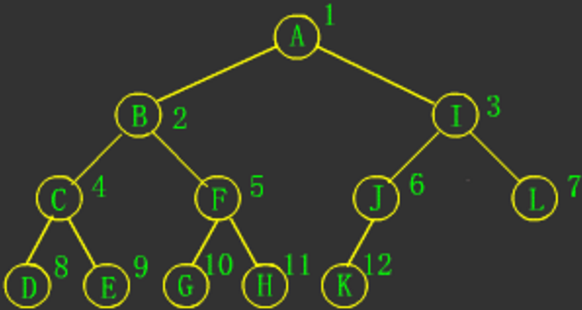
定义:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
扩展资料:
满二叉树:美国以及国际上所定义的满二叉树和国内的定义不同,美国NIST给出的定义为:满二叉树的任意节点,要么度为0,要么度为2.换个说法即要么为叶子结点,要么同时具有左右孩子。霍夫曼树是符合这种定义的,满足国际上定义的满二叉树,但是不满足国内的定义。
完全二叉树:可以根据公式进行推导,假设n0是度为0的结点总数(即叶子结点数),n1是度为1的结点总数,n2是度为2的结点总数,则 :
①n= n0+n1+n2 (其中n为完全二叉树的结点总数);又因为一个度为2的结点会有2个子结点,一个度为1的结点会有1个子结点,除根结点外其他结点都有父结点。
②n= 1+n1+2*n2 ;由①、②两式把n2消去得:n= 2*n0+n1-1,由于完全二叉树中度为1的结点数只有两种可能0或1,由此得到n0=n/2 或 n0=(n+1)/2。
简便来算,就是 n0=n/2,其中n为奇数时(n1=0)向上取整;n为偶数时(n1=1)。可根据完全二叉树的结点总数计算出叶子结点数。