前言
接着第四章
本篇总结自《算法笔记》4.3 递归
正文
知识点1:递归
递归的简单定义:函数反复调用自身,每次调用都把问题范围缩小,一直缩小到可以直接得到边界数据,然后再在返回的路上求出对应的解。
递归的逻辑中两个重要概念:
1 递归边界
2 递归式(递归调用)
其中的递归式是将原问题分成若干子问题的手段,递归边界则是分解的尽头。(如果没有尽头就会无限分解)
经典例子1️⃣:使用递归求解n的阶乘
n! = 1*2*3*4*5……(n-1)*n
写成递推形式:n! = (n-1)! * n 【规模从n变成了n-1】
用F(n)表示n!的递推形式:F(n) = F(n-1) * n
找边界:把规模一直减小到F(0)即0!,而0!=1,所以可以把F(0)=1作为递归的边界。

经典例子2️⃣:求Fibonacci数列的第n项
斐波那契数列满足F(0)=1,F(1)=1,F(n)=F(n-1)+F(n-2) (n≥2)

经典例子3️⃣:全排列(Full Permutation)
一个数列所有的排列方式的集合称为全排列。
【举例】如1,2,3的全排列:(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1);(按字典序)
【目的】按字典序从小到大输出全排列:其中(a1,a2,...an)的字典序小于(b1,b2,...bn),是指存在一个i,使得a1=b1,a2=b2,……,ai<bi成立;
#include<cstdio> const int maxn = 11; // max number int n, p[maxn], hashTable[maxn] = {false}; // p: Now permutation, hashTable: Record whether x has been placed in p void generateP(int index) { if(index == n + 1) // recursion boundary { for(int i = 1; i <= n; i++) // print result { printf("%d", p[i]); } printf(" "); return; } for(int x = 1; x <= n; x++) { if(hashTable[x] == false) // x hasn't been used { p[index] = x; // use x (place x in p) hashTable[x] = true; // x has been used generateP(index + 1); // recursion (resolve the sub-problems when p[index] = x) hashTable[x] = false; // restore the x (resolved) } } } int main() { n = 3; // want to print 1~3 full permutation generateP(1); // recursion start from 1 return 0; }
经典例子4️⃣:n皇后问题
#include<cstdio> #include<cmath> #include<algorithm> using namespace std; const int maxn = 11; int n, P[maxn], hashTable[maxn] = {false};
// p: 当前排列, hashTable: 记录x是否已经放入p
int counter = 0; void generateP1(int index){ /* 递归边界 生成一个排列 */ if(index == n + 1){ bool flag = true; // 当前排列合法 /* 遍历任意两个皇后 */ for(int i = 1; i <= n; i++){ for(int j = i + 1; j <= n; j++){ for(int j = i + 1; j <= n; j++){ if(abs(i - j) == abs(P[i] - P[j])){ // 在同一对角线上 flag = false; // 冲突 } } } } if(flag) counter++; return; } for(int x = 1; x <= n; x++){ if(hashTable[x] == false){ P[index] = x; hashTable[x] = true; generateP1(index + 1); hashTable[x] = false; } } } void generateP2(int index){ /* 递归边界 */ if(index == n + 1){ counter++; return; } /* 遍历行 */ for(int x = 1; x <= n; x++){ /* 若第x行还没皇后 */ if(hashTable[x] == false){ bool flag = true; // flag为true表示不会与之前的皇后冲突 /* 遍历之前的皇后 */ for(int pre = 1; pre < index; pre++){ /* 判断是否冲突 */ if(abs(index - pre) == abs(x - P[pre])){ flag = false; // 冲突(在同一对角线) break; // 跳出循环 } } /* 无冲突则放置皇后 */ if(flag) { P[index] = x; hashTable[x] = true; //占用第x行 generateP2(index + 1); // 处理下一行(子问题) hashTable[x] = false; // 子问题都处理完了,还原第x行状态 } } } } int main(){ n = 8; // 棋盘大小 n*n generateP2(1); //从P[1]开始填 printf("%d ", counter); return 0; }
【注】n皇后问题方法总结
普通枚举(暴力):随意选取空位摆放。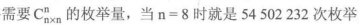 ;
;
全排列(暴力):按列/行逐个摆下去。把所有的子问题都遍历处理到底,最后再检测是否符合要求(见generateP1方法)
全排列(回溯):按列/行逐个摆下去。过程中增加检测功能,即若继续放已经不再可能达成目标,则不再遍历处理子问题,立即返回(见generateP2方法)
普通枚举要处理行冲突、列冲突、对角线冲突,全排列只需处理对角线冲突
“递归”总结到此为止;
“贪心”见下一篇;
加油