实验9 图及图的操作实验
--博客后半部分有程序的所有代码--
1、图邻接矩阵存储结构表示及基本操作算法实现
(1)邻接矩阵存储结构类定义:
#include "SeqList.h" //包含动态数组结构的顺序表类 #include "SeqQueue.h" //包含静态数组结构的顺序队列类 typedef char VerT; //定义邻接矩阵图类中的VerT class AdjMWGraph { private: SeqList Vertices; //顶点顺序表 int Edge[MaxVertices][MaxVertices]; //边权值数组 double numOfEdges; //边的个数 void DepthFirstSearch(const int v, int visited[]); void BroadFirstSearch(const int v, int visited[]); public: AdjMWGraph(const int sz=MaxVertices); //构造函数 ~AdjMWGraph(void){}; //析构函数 int NumOfVertices(void) //取顶点个数 {return Vertices.Size();} int NumOfEdges(void) //取边的个数 {return numOfEdges;} Void Show(); //输出邻接矩阵结果 VerT GetValue(const int v); //取顶点数值 int GetWeight(const int v1, const int v2); //取边的权值 void InsertVertex(const VerT &vertex); //插入顶点 void InsertWayEdge(const int v1, const int v2, int weight);//插入边 void InsertNoWayEdge(const int v1, const int v2, int weight);//插入边 void DeleteVertex(const int v); //删除顶点 void DeleteEdge(const int v1, const int v2); //删除边 int GetFirstNeighbor(const int v); //取第一个邻接顶点 int GetNextNeighbor(const int v1, const int v2);//取下一个邻接顶点 void DepthFirstSearch(); //深度优先遍历 void BroadFirstSearch(); //广度优先遍历 }; struct RowColWeight //网的结构体 { int row; //行下标 int col; //列下标 int weight; //权值 }; struct RowCol //图的结构体 { int row; //行下标 int col; //列下标 };
(2)创建邻接矩阵算法
①创建无向图邻接矩阵算法:
void CreatNoWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e) { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) { if(E[k].row>E[k].col) { cout<<"无向图参数输入错误"; exit(0); } G.InsertNoWayEdge(E[k].row, E[k].col, 1); G.InsertNoWayEdge(E[k].col, E[k].row, 1); } }
②创建无向网邻接矩阵算法:
void CreatNoWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e) { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) { if(E[k].row>E[k].col) { cout<<"无向网参数输入错误"; exit(0); } G.InsertNoWayEdge(E[k].row, E[k].col, E[k].weight); G.InsertNoWayEdge(E[k].col, E[k].row, E[k].weight); }
③创建有向图邻接矩阵算法:
void CreatWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e) //在图G中插入n个顶点V 和 e条边E { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) G.InsertWayEdge(E[k].row, E[k].col,1); }
④创建有向网邻接矩阵算法:
void CreatWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e) //在图G中插入n个顶点V 和 e条边E { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) G.InsertWayEdge(E[k].row, E[k].col, E[k].weight); }
(3)输出邻接矩阵结果算法
int AdjMWGraph::Show() { for(int i=0;i<Vertices.Size();i++) { for(int j=0;j<Vertices.Size();j++) { int a=GetWeight(i,j); if(a==MaxWeight) cout<<"∞ "; else cout<<a<<" "; } cout<<endl; } }
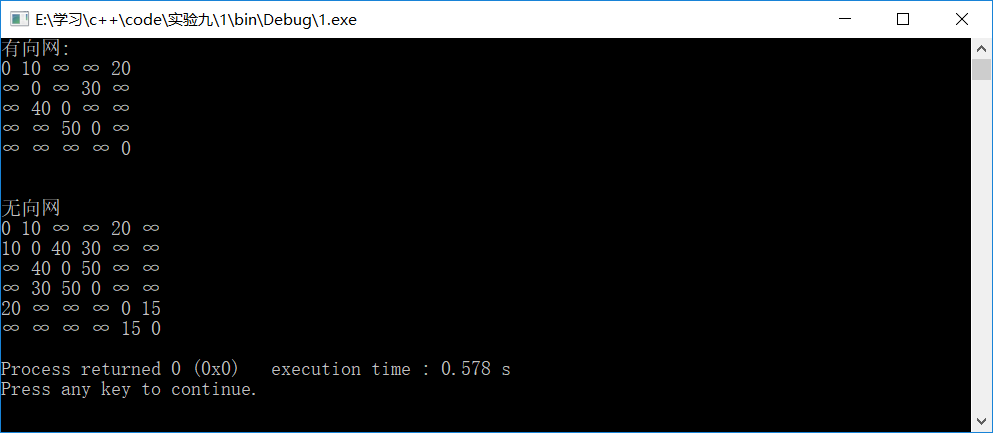
测试数据:
int main() { AdjMWGraph g,f; char a[] = {'A','B','C','D','E'}; char b[] = {'A','B','C','D','E','F'}; RowColWeight r1[] ={{0,1,10},{0,4,20},{1,3,30},{2,1,40},{3,2,50}}; RowColWeight r2[] ={{0,1,10},{0,4,20},{1,3,30},{1,2,40},{2,3,50},{4,5,15}}; int n1,n2,e1,e2; n1=sizeof(a)/sizeof(a[0]); n2=sizeof(b)/sizeof(b[0]); e1=sizeof(r1)/sizeof(r1[0]); e2=sizeof(r2)/sizeof(r2[0]); CreatWayWeb(g, a, n1, r1, e1); //创建有向网 CreatNoWayWeb(f, b, n2, r2, e2); //创建无向网 cout<<"有向网:"<<endl; g.Show(); cout<<" 无向网"<<endl; f.Show(); return 0; }
结果:
2、图的遍历递归算法
(1)(存储结构为邻接矩阵)深度优先遍历算法
void AdjMWGraph::DepthFirstSearch(const int v, int visited[]) //连通图G以v为初始顶点序号 //数组visited标记了相应顶点是否已访问过, // 0表示未访问,1表示已访问 { cout<<GetValue(v)<<" "; //访问该顶点 visited[v] = 1; //置已访问标记 //取第一个邻接顶点 int w = GetFirstNeighbor(v); //当邻接顶点存在时循环 while(w != -1) { if(! visited[w]) DepthFirstSearch(w, visited); //递归 w = GetNextNeighbor(v, w); //取下一个邻接顶点 } } void AdjMWGraph::DepthFirstSearch() { int *visited = new int[NumOfVertices()]; //初始化访问标记 for(int i = 0; i < NumOfVertices(); i++) visited[i] = 0; //深度优先遍历 for(int i = 0; i < NumOfVertices(); i++) if(! visited[i]) DepthFirstSearch(i, visited); delete []visited; }
有向/无向网的测试结果:
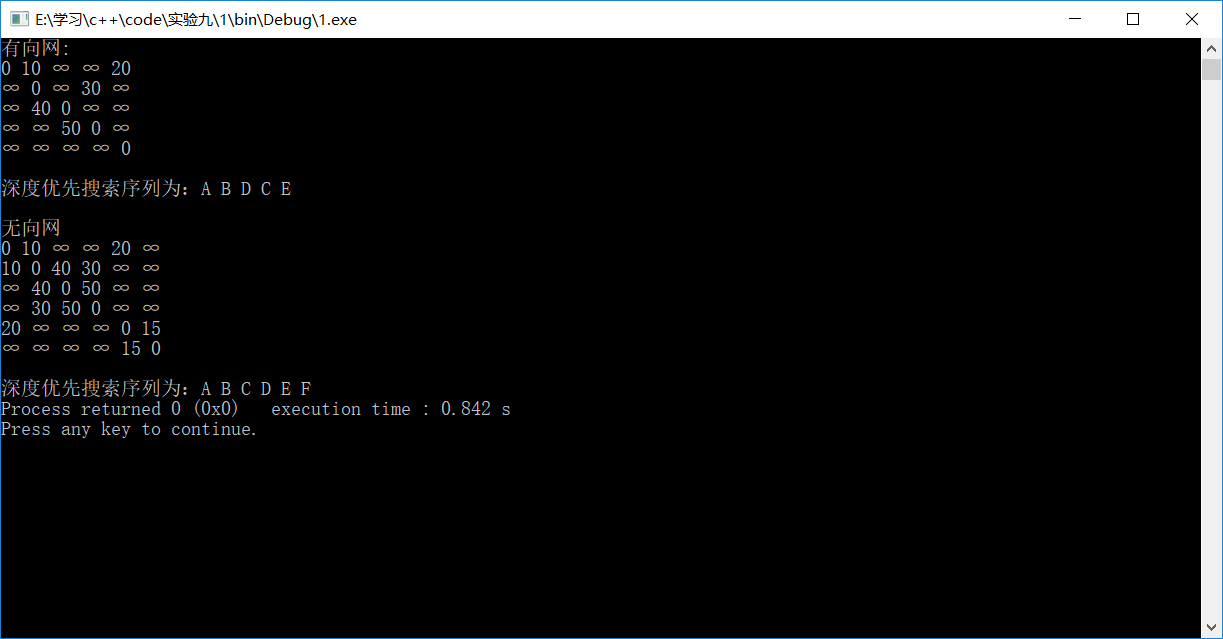
(2)广度优先遍历算法
void AdjMWGraph::BroadFirstSearch(const int v, int visited[]) { VerT u; int w; SeqQueue queue; //定义队列 cout<<GetValue(v)<<" "; //访问该顶点 visited[v] = 1; //置已访问标记 queue.Append(v); //顶点v入队列 while(queue.NotEmpty()) //队列非空时循环 { u = queue.Delete(); //出队列 w = GetFirstNeighbor(u); //取顶点u的第一个邻接顶点 while(w != -1) //邻接顶点存在时 { if(!visited[w]) //若该顶点没有访问过 { cout<<GetValue(w)<<" "; //访问该顶点 visited[w] = 1; //置已访问标记 queue.Append(w); //顶点w入队列 } w = GetNextNeighbor(u, w); } } } void AdjMWGraph::BroadFirstSearch() //非连通图G访问操作为Visit()的广度优先遍历 { int *visited = new int[NumOfVertices()]; for(int i = 0; i < NumOfVertices(); i++) visited[i] = 0; for(int i = 0; i < NumOfVertices(); i++) if(!visited[i]) BroadFirstSearch(i, visited); delete []visited; }
有向网/无向网的测试结果:

最后附上整体代码结构与结果
AdjMWGraph.h
#include "SeqList.h" //包含动态数组结构的顺序表类 #include "SeqQueue.h" //包含静态数组结构的顺序队列类 typedef char VerT; //定义邻接矩阵图类中的VerT class AdjMWGraph { private: SeqList Vertices; //顶点顺序表 int Edge[MaxVertices][MaxVertices]; //边权值数组 double numOfEdges; //边的个数 void DepthFirstSearch(const int v, int visited[]); void BroadFirstSearch(const int v, int visited[]); public: AdjMWGraph(const int sz=MaxVertices); //构造函数 ~AdjMWGraph(void){}; //析构函数 void Show(); //输出邻接矩阵结果 int NumOfVertices(void) //取顶点个数 {return Vertices.Size();} int NumOfEdges(void) //取边的个数 {return numOfEdges;} VerT GetValue(const int v); //取顶点数值 int GetWeight(const int v1, const int v2); //取边的权值 void InsertVertex(const VerT &vertex); //插入顶点 void InsertWayEdge(const int v1, const int v2, int weight);//插入边 void InsertNoWayEdge(const int v1, const int v2, int weight);//插入边 void DeleteVertex(const int v); //删除顶点 void DeleteEdge(const int v1, const int v2); //删除边 int GetFirstNeighbor(const int v); //取第一个邻接顶点 int GetNextNeighbor(const int v1, const int v2);//取下一个邻接顶点 void DepthFirstSearch(); //深度优先遍历 void BroadFirstSearch(); //广度优先遍历 }; AdjMWGraph::AdjMWGraph(const int sz): Vertices(sz) //构造函数 ,构造顶点个数为sz个,没有边的图 { for(int i = 0; i < sz; i++) for(int j = 0; j < sz; j++) { if(i == j) Edge[i][j] = 0; else Edge[i][j] = MaxWeight; } // MaxWeight权值的无穷大 numOfEdges = 0; } VerT AdjMWGraph::GetValue(const int v) //取顶点v的数值 { if(v < 0 || v >= Vertices.Size()) { cout << "参数v越界出错!" << endl; exit(0); } return Vertices.GetData(v); } int AdjMWGraph::GetWeight(const int v1, const int v2) //取起始顶点为v1、终止顶点为 v2的边的权值 { if(v1 < 0 || v1 >= Vertices.Size() || v2 < 0 || v2 >= Vertices.Size()) { cout << "参数v1或v2越界出错!" << endl; exit(0); } return Edge[v1][v2]; } void AdjMWGraph::InsertVertex(const VerT &vertex) //插入顶点vertex //把顶点vertex插入到顺序表的当前表尾位置 { Vertices.Insert(vertex, Vertices.Size()); } void AdjMWGraph::InsertWayEdge(const int v1, const int v2, int weight) //插入一条起始顶点为v1、终止顶点为 v2、权值为weight的边 { if(v1 < 0||v1>=Vertices.Size()||v2 < 0||v2 >=Vertices.Size()) { cout << "参数v1或v2越界出错!" << endl; exit(0); } Edge[v1][v2] = weight; //插入边 numOfEdges++; //边的个数加1 }void AdjMWGraph::InsertNoWayEdge(const int v1, const int v2, int weight) //插入一条起始顶点为v1、终止顶点为 v2、权值为weight的边 { if(v1 < 0||v1>=Vertices.Size()||v2 < 0||v2 >=Vertices.Size()) { cout << "参数v1或v2越界出错!" << endl; exit(0); } Edge[v1][v2] = weight; //插入边 numOfEdges+=0.5; //边的个数加0.5 } void AdjMWGraph::DeleteVertex(const int v) //删除顶点v { //删除所有包含顶点v的边 for(int i = 0; i < Vertices.Size(); i++) for(int j = 0; j < Vertices.Size(); j++) if((i == v || j == v) && i != j && Edge[i][j] > 0 && Edge[i][j] < MaxWeight) { Edge[i][j] = MaxWeight; //把该边的权值置为无穷大 numOfEdges--; //边的个数减1 } Vertices.Delete(v); //删除顶点v } void AdjMWGraph::DeleteEdge(const int v1, const int v2) //删除一条起始顶点为v1、终止顶点为 v2的边 { if(v1 < 0 || v1 >Vertices.Size()||v2<0||v2>Vertices.Size()) { cout<<Vertices.Size(); cout << "参数v1或v2出错!" << endl; exit(0); } if(Edge[v1][v2] == MaxWeight ) { cout << "该边不存在!" << endl; exit(0); } Edge[v1][v2] = MaxWeight; //把该边的权值置为无穷大 numOfEdges--; //边的个数减1 } int AdjMWGraph::GetFirstNeighbor(const int v) //取顶点v的第一个邻接顶点。若存在返回该顶点的下标序号,否则返回-1 { if(v< 0 || v> Vertices.Size()) { cout << "参数v1越界出错!" << endl; exit(0); } for(int col = 0; col <=Vertices.Size(); col++) if(Edge[v][col] > 0 && Edge[v][col] < MaxWeight) return col; return -1; } int AdjMWGraph::GetNextNeighbor(const int v1, const int v2) //取顶点v1的邻接顶点v2后的邻接顶点 //若存在返回该顶点的下标序号,否则返回-1 { if(v1 < 0 || v1 > Vertices.Size() || v2 < 0 || v2 >Vertices.Size()) { cout << "参数v1或v2越界出错!" << endl; exit(0); } for(int col = v2+1; col < Vertices.Size(); col++) if(Edge[v1][col] > 0 && Edge[v1][col] < MaxWeight) return col; return -1; } void AdjMWGraph::DepthFirstSearch(const int v, int visited[]) //连通图G以v为初始顶点序号 //数组visited标记了相应顶点是否已访问过, // 0表示未访问,1表示已访问 { cout<<GetValue(v)<<" "; //访问该顶点 visited[v] = 1; //置已访问标记 //取第一个邻接顶点 int w = GetFirstNeighbor(v); //当邻接顶点存在时循环 while(w != -1) { if(! visited[w]) DepthFirstSearch(w, visited); //递归 w = GetNextNeighbor(v, w); //取下一个邻接顶点 } } void AdjMWGraph::DepthFirstSearch() { int *visited = new int[NumOfVertices()]; //初始化访问标记 for(int i = 0; i < NumOfVertices(); i++) visited[i] = 0; //深度优先遍历 for(int i = 0; i < NumOfVertices(); i++) if(! visited[i]) DepthFirstSearch(i, visited); delete []visited; } void AdjMWGraph::BroadFirstSearch(const int v, int visited[]) { VerT u; int w; SeqQueue queue; //定义队列 cout<<GetValue(v)<<" "; //访问该顶点 visited[v] = 1; //置已访问标记 queue.Append(v); //顶点v入队列 while(queue.NotEmpty()) //队列非空时循环 { u = queue.Delete(); //出队列 w = GetFirstNeighbor(u); //取顶点u的第一个邻接顶点 while(w != -1) //邻接顶点存在时 { if(!visited[w]) //若该顶点没有访问过 { cout<<GetValue(w)<<" "; //访问该顶点 visited[w] = 1; //置已访问标记 queue.Append(w); //顶点w入队列 } w = GetNextNeighbor(u, w); } } } void AdjMWGraph::BroadFirstSearch() //非连通图G访问操作为Visit()的广度优先遍历 { int *visited = new int[NumOfVertices()]; for(int i = 0; i < NumOfVertices(); i++) visited[i] = 0; for(int i = 0; i < NumOfVertices(); i++) if(!visited[i]) BroadFirstSearch(i, visited); delete []visited; } void AdjMWGraph::Show() { for(int i=0;i<Vertices.Size();i++) { for(int j=0;j<Vertices.Size();j++) { int a=GetWeight(i,j); if(a==MaxWeight) cout<<"∞ "; else cout<<a<<" "; } cout<<endl; } }
CreatAdjMWGraph.h
struct RowColWeight //网的结构体 { int row; //行下标 int col; //列下标 int weight; //权值 }; struct RowCol //图的结构体 { int row; //行下标 int col; //列下标 }; void CreatWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e) //在图G中插入n个顶点V 和 e条边E { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) G.InsertWayEdge(E[k].row, E[k].col, E[k].weight); } void CreatNoWayWeb(AdjMWGraph &G, DataType V[],int n,RowColWeight E[], int e) { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) { if(E[k].row>E[k].col) { cout<<"无向网参数输入错误"; exit(0); } G.InsertNoWayEdge(E[k].row, E[k].col, E[k].weight); G.InsertNoWayEdge(E[k].col, E[k].row, E[k].weight); } } void CreatWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e) //在图G中插入n个顶点V 和 e条边E { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) G.InsertWayEdge(E[k].row, E[k].col,1); } void CreatNoWayGraph(AdjMWGraph &G, DataType V[],int n,RowCol E[], int e) { //在图G中插入n个顶点 for(int i = 0; i < n; i++) G.InsertVertex(V[i]); //在图G中插入e条边 for(int k = 0; k < e; k++) { if(E[k].row>E[k].col) { cout<<"无向图参数输入错误"; exit(0); } G.InsertNoWayEdge(E[k].row, E[k].col, 1); G.InsertNoWayEdge(E[k].col, E[k].row, 1); } }
SeqList.h
class SeqList { protected: DataType *list; //数组 int maxSize; //最大元素个数 int size; //当前元素个数 public: SeqList(int max=0); //构造函数 ~SeqList(void); //析构函数 int Size(void) const; //取当前数据元素个数 void Insert(const DataType& item, int i);//插入 DataType Delete(const int i); //删除 DataType GetData(int i) const; //取数据元素 }; SeqList::SeqList(int max) //构造函数 { maxSize = max; size = 0; list = new DataType[maxSize]; } SeqList::~SeqList(void) //析构函数 { delete []list; } int SeqList::Size(void) const //取当前数据元素个数 { return size; } void SeqList::Insert(const DataType& item, int i) //插入 //在指定位置i前插入一个数据元素item { if (size == maxSize) { cout << "顺序表已满无法插入!" << endl; exit(0); } if(i < 0 || i > size) //参数正确与否判断 { cout << "参数i越界出错!" << endl; exit(0); } //从size-1至i逐个元素后移 for(int j = size; j > i; j--) list[j] = list[j-1]; list[i] = item; //在i位置插入item size++; //当前元素个数加1 } DataType SeqList::Delete(const int i) //删除 //删除指定位置i的数据元素,删除的元素由函数返回 { if (size == 0) { cout << "顺序表已空无元素可删!" << endl; exit(0); } if(i < 0 || i > size - 1) //参数正确与否判断 { cout<<"参数i越界出错!"<<endl; exit(0); } DataType x = list[i]; //取到要删除的元素 //从i+1至size-1逐个元素前移 for(int j = i;j < size-1; j++) list[j] = list[j+1]; size--; //当前元素个数减1 return x; //返回删除的元素 } DataType SeqList::GetData(int i) const //取数据元素 //取位置i的数据元素,取到的数据元素由函数返回 { if(i < 0 || i > size - 1) //参数正确与否判断 { cout << "参数i越界出错!" << endl; exit(0); } return list[i]; //返回取到的元素 }
SeqQueue.h
class SeqQueue{ private: DataType data[20]; //顺序队列数组 int front; //队头指示器 int rear; //队尾指示器 int count; //元素个数计数器 int maxsize; public: SeqQueue(); //构造函数 ~SeqQueue(void){}; //析构函数 void Append(const DataType& item); //入队列 int NotEmpty(void)const //非空否 {return count!=0;} DataType Delete(void); //出队列 }; SeqQueue::SeqQueue() { front=rear=0; count=0; }; void SeqQueue::Append(const DataType& item) //入队列 //把数据元素item插入队列作为当前的新队尾 { if(count>0&&front==rear) { cout<<"队列已满!"<<endl; exit(0); } data[rear]=item; //把元素item加在队尾 rear=(rear+1) % maxsize; //队尾指示器加1 count++; //计数器加1 } DataType SeqQueue::Delete(void) //出队列 //把队头元素出队列,出队列元素由函数返回 { if(count==0) { cout<<"队列已空!"<<endl; exit(0); } DataType temp=data[front]; //保存原队头元素 front=(front+1) % maxsize; //队头指示器加1 count--; //计数器减1 return temp; //返回原队头元素 }
main.cpp
#include <iostream> #include <stdlib.h> using namespace std; typedef char VerT; //定义邻接矩阵图类中的VerT typedef char DataType; //定义顺序表类中的DataType const int MaxVertices = 100; //定义最大顶点个数 const int MaxWeight = 10000; //定义权值的无穷大 #include "AdjMWGraph.h"//包含邻接矩阵的图类 #include "CreatAdjMWGraph.h"//包含邻接矩阵图的创建函数 int main() { AdjMWGraph g,f; char a[] = {'A','B','C','D','E'}; char b[] = {'A','B','C','D','E','F'}; RowColWeight r1[] ={{0,1,10},{0,4,20},{1,3,30},{2,1,40},{3,2,50}}; RowColWeight r2[] ={{0,1,10},{0,4,20},{1,3,30},{1,2,40},{2,3,50},{4,5,15}}; int n1,n2,e1,e2; n1=sizeof(a)/sizeof(a[0]); n2=sizeof(b)/sizeof(b[0]); e1=sizeof(r1)/sizeof(r1[0]); e2=sizeof(r2)/sizeof(r2[0]); CreatWayWeb(g, a, n1, r1, e1); //创建有向网 CreatNoWayWeb(f, b, n2, r2, e2); //创建无向网 cout<<"有向网:"<<endl; g.Show(); cout << " 顶点个数为:" << g.NumOfVertices(); cout << " 边的条数为:" << g.NumOfEdges(); cout << " 深度优先搜索序列为:"; g.DepthFirstSearch(); cout << " 广度优先搜索序列为:"; g.BroadFirstSearch(); cout<<" 无向网"<<endl; f.Show(); cout << " 顶点个数为:" << f.NumOfVertices(); cout << " 边的条数为:" << f.NumOfEdges(); cout << " 深度优先搜索序列为:"; f.DepthFirstSearch(); cout << " 广度优先搜索序列为:"; f.BroadFirstSearch(); return 0; }
最终结果
