第一种解法来自:http://blog.csdn.net/tianshuai11/article/details/7797897,
- /*
- Author: Mcdragon
- Date: 15-07-11 21:17
- Description: 求一个字符串中连续出现次数最多的子串.
- 基本算法描述:
- 给出一个字符串abababa
- 1.穷举出所有的后缀子串
- substrs[0] = abababa;
- substrs[1] = bababa;
- substrs[2] = ababa;
- substrs[3] = baba;
- substrs[4] = aba;
- substrs[5] = ba;
- substrs[6] = a;
- 2.然后进行比较
- substrs[0]比substrs[1]多了一个字母,如果说存在连续匹配的字符,那么
- substrs[0]的第1个字母要跟substrs[1]首字母匹配,同理
- substrs[0]的前2个字母要跟substrs[2]的前2个字母匹配(否则不能叫连续匹配)
- substrs[0]的前n个字母要跟substrs[n]的前n个字母匹配.
- 如果匹配的并记下匹配次数.如此可以求得最长连续匹配子串.
- */
- #include <iostream>
- #include <string>
- #include <vector>
- using namespace std;
- pair<int, string> fun(const string &str)
- {
- vector<string> substrs;
- int maxcount = 1, count = 1;
- string substr;
- int i, len = str.length();
- for(i=0; i<len; ++i)
- substrs.push_back(str.substr(i, len-i));
- /*for(i=0; i<len; ++i)
- cout << substrs[i] << endl;*/
- for(i=0; i<len; ++i)
- {
- for(int j=i+1; j<len; ++j)
- {
- count = 1;
- if(substrs[i].substr(0, j-i) == substrs[j].substr(0,j-i))
- {
- ++count;
- for(int k=j+(j-i); k<len; k+=j-i)
- {
- if (substrs[i].substr(0,j-i) == substrs[k].substr(0, j-i))
- ++count;
- else
- break;
- }
- if(count > maxcount)
- {
- maxcount = count;
- substr=substrs[i].substr(0, j-i);
- }
- }
- }
- }
- return make_pair(maxcount, substr);
- }
- int main()
- {
- pair<int, string> rs;
- string str="abababababaccccc";
- rs = fun(str);
- cout << rs.second<<':'<<rs.first<<'\n';
- system("pause");
- return 0;
- }
第二种 感觉是用空间来换取时间,复杂度是O(n^2). http://blog.csdn.net/tianshuai11/article/details/7797897
一,考虑边界问题。
二,实现优化笛卡尔积组合,
总体我是这样想的:就是纵向切出字符串的连续组合集合,在横向一对一跳跃比较集合元素。
例如:abcbcabc
一,纵向切:
得到所有字符串组合,注意:这里要求的是最多连续子字符串,其实就是优化笛卡尔积的原则,也是边界。
1----从a开始切:(字符串为abcbcabc )
第一次切出a子字符串,得到: a和bcbcabc,
第二次切出ab子字符串,得到: ab和cbcabc,
第三次切出abc子字符串,得到: abc和bcabc,
第四次切出abcb子字符串,得到: abcb和cabc,
第五次切出abcbc子字符串,得到: abcbc和abc,
第六次切出abcbca子字符串,得到: abcbca和bc,
第七次切出abcbcab子字符串,得到: abcbcab和c,
第八次切出abcbcabc子字符串,得到: abcbcabc,
得到a1集合数组(且为数组吧)
元素为:a, ab, abc, ......
2---再从b开始切::(字符串为abcbcabc )
第一次切出b子字符串,得到: b和cbcabc,
第二次切出bc子字符串,得到: bc和bcabc,
第三次切出bcb子字符串,得到: bcb和cabc,
第四次切出bcbc子字符串,得到: bcbc和abc,
第五次切出bcbca子字符串,得到: bcbca和bc,
第六次切出bcbcab子字符串,得到: bcbcab和c,
第七次切出bcbcabc子字符串,得到: bcbcabc
得到b2集合数组(且为数组吧)
元素为:b, bc, bcb ,......
3---再从c开始切: (字符串为abcbcabc )
第一次切出c子字符串,得到: c和bcabc,
第二次切出cb子字符串,得到: cb和cabc,
第三次切出cbc子字符串,得到: cbc和abc,
第四次切出cbca子字符串,得到: cbca和bc,
第五次切出cbcab子字符串,得到: cbcab和c,
第六次切出cbcabc子字符串,得到: cbcabc
得到b3集合数组(且为数组吧)
元素为:c, cb, cbc ,......
4----再从b开始切: (字符串为abcbcabc )
第一次切出b子字符串,得到: b和cabc,
第二次切出bc子字符串,得到: bc和abc,
第三次切出bca子字符串,得到: bca和bc,
第四次切出bcab子字符串,得到: bcab和c,
第五次切出bcabc子字符串,得到: bcabc
得到b4集合数组(且为数组吧)
元素为:b, bc, bca ,......
5----再从c开始切: (字符串为abcbcabc )
第一次切出c子字符串,得到: c和abc,
第二次切出ca子字符串,得到: ca和bc,
第三次切出cab子字符串,得到: cab和c,
第四次切出cabc子字符串,得到: cabc
得到c5集合数组(且为数组吧)
元素为:c, ca, cab ,......
6----再从a开始切: (字符串为abcbcabc )
第一次切出a子字符串,得到: a和bc,
第二次切出ab子字符串,得到: ab和c,
第三次切出abc子字符串,得到: abc,
得到a6集合数组(且为数组吧)
元素为:a, ab, abc
7----再从b开始切: (字符串为abcbcabc )
第一次切出b子字符串,得到: b和c,
第二次切出bc子字符串,得到: bc,
得到b7集合数组(且为数组吧)
元素为:b, bc
8----再从c开始切: (字符串为abcbcabc )
第一次切出c子字符串,得到: c
得到c8集合数组(且为数组吧)
元素为:c
2,横向比:
将a的所有切点按切的顺序保存到称为a1集合数组中(且为数组吧)
将b的所有切点按切的顺序保存到称为b2集合数组中(且为数组吧)
。。。依次类推到完。
得到如下8个集合:(字符串为abcbcabc )
行数/列数 1 2 3 4 5 6 7 8
将a1集合,b2集合。。。等全部集合横向比较:
即将列1比较,列2比较跳跃1行比较,列3跳跃2行比较,列3跳跃3行比较。。。。到完;因为要求的是最多连续子字符串,所以要跳跃!
得到相同字符串记数最大值,即求出出现次数最多的子串。
比较方式:
正于前面所说,要求的是最多连续子字符串。其实就是优化笛卡尔积的原则,也是边界。所以我们要做的是将所有集合一对一比较,不是多对多或其他(更简单的理由:位数不同,无需比较)。
多位子字符串一对一比较时候,例如 ab属于a集合和b集合的bc比较,显然没有意义。需要跳跃比较(且这样说吧,呵呵)。跳跃是有规律的。很显然就不说了。
之所以纵切,是为了解决横比较带来的优化问题
- #include<iostream>
- #include<string>
- #include<vector>
- using namespace std;
- pair<int,string> fun(const string &str)
- {
- vector<string> substrs;
- int maxcount=1,count =1;
- string substr;
- int i,len = str.length();
- for(i =0;i<len;++i)
- {
- substrs.push_back(str.substr(i,len-i));// // 把abcbcbcabc,bcbcbcabc,cbcbcabc, bcbcabc,cbcabc,bcabc,cabc,abc,bc,c一次放入容器中
- }
- for(i =0;i<len;i++)
- {
- for(int j =i+1;j<len;j++)
- {
- count =1;
- if(substrs[i].substr(0,j-i)==substrs[j].substr(0,j-i))//第一次循环先单个字符比较,然后再两个,三个字符比较
- {
- ++count;
- for(int k =j+(j-i);k<len;k +=j-i)
- {
- if(substrs[i].substr(0,j-i)==substrs[k].substr(0,j-i))//如果前面比较成功,则需要后面跳跃处理
- ++count;
- else
- break;
- }
- if(count>maxcount)
- {
- maxcount =count;
- substr =substrs[j].substr(0,j-i);
- }
- }
- }
- }
- return make_pair(maxcount,substr);
- }
- int main()
- {
- string str;
- pair<int, string>rs;
- while(cin>>str)
- {
- rs=fun(str);
- cout<<rs.second<<rs.first<<'\n';
- }
- return 0;
- }
第三种:O(NLOGN) http://www.cppblog.com/superKiki/archive/2010/05/15/115421.aspx
例8:重复次数最多的连续重复子串(spoj687,pku3693)
给定一个字符串,求重复次数最多的连续重复子串。
算法分析:
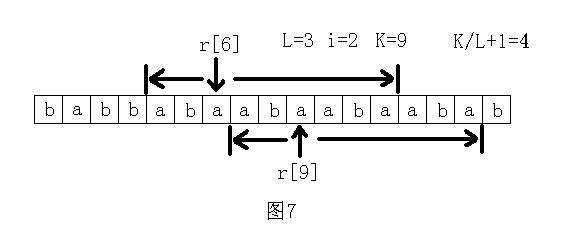
先穷举长度L,然后求长度为L的子串最多能连续出现几次。首先连续出现1次是肯定可以的,所以这里只考虑至少2次的情况。假设在原字符串中连续出现2次,记这个子字符串为S,那么S肯定包括了字符r[0],r[L],r[L*2],r[L*3],……中的某相邻的两个。所以只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远,记这个总长度为K,那么这里连续出现了K/L+1次。最后看最大值是多少。如图7所示。
穷举长度L的时间是n,每次计算的时间是n/L。所以整个做法的时间复杂度是O(n/1+n/2+n/3+……+n/n)=O(nlogn)。
第四种:传闻中的O(N) 应该是错误的
http://hi.baidu.com/inydprdilpbdepq/item/c5ee4d2d6d290e1609750827