交换排序
冒泡
思路:
1、外层循环是遍历每个元素,每次都放置好一个元素。
2、内层循环将剩余序列中所有元素两两比较,将较大的放在后面。
3、重复第二步,直到只剩下一个数。
如果有n个元素,则第一次循环进行n-1次比较,第二次循环进行n-2次,…………,第n-j次循环过后,会按大小顺序排出j个较大的数。

写成代码:
1、设置循环次数。
2、设置开始比较的位数,和结束的位数。
3、两两比较,将最小的放到前面去。
4、重复2、3步,直到循环次数完毕。
/**
* 最优的情况也就是开始就已经排序好序了,这是循环n-1次每次没有交换动作而退出,则时间花销为:n(n-1)/2;所以最优的情况时间复杂度为:O( n^2 );
* 最坏是完全逆序(其中比上面最优的情况所花的时间就是在于交换元素的三个步骤),即需要加上交换移动次数
* 3n(n-1)/2次,所以时间复杂度也是O(N^2)。
*
* 该算法中空间复杂度一般是看交换元素时所使用的辅助空间,即交换元素时那个临时变量所占的内存空间。
* 最优的空间复杂度就是开始元素顺序已经排好了,则空间复杂度为:0;
* 最差的空间复杂度就是开始元素逆序排序了,则空间复杂度为:O(n);
* 平均的空间复杂度为:O(1);
*
* PS:想想使最优的时间复杂度为:O(n)的写法?
* https://blog.csdn.net/yuzhihui_no1/article/details/44339711
*/
@Test
public void bubble(){
int[] a = {3,5,12,4,1,4,1,8};
for(int i=0; i<a.length-1; i++){
for(int j=0; j<a.length-1-i; j++){
if(a[j] > a[j+1]){
ArrUtil.swap(a, j+1, j);
}
System.out.println(Arrays.toString(a));
}
}
}
快速排序
思路:
1、选择第一个数为p,称为 "基准"(pivot);
2、指针i一步一步从左往右寻找大于基数p的数字,指针j从右往左寻找小于基数p的数字,i、j都找到后将两个位置的数字进行交换,然后继续前进比较、交换,直到i>=j结束循环,然后将基准数 p和i(或j)位置的数进行交换,即完成一趟快排,这个称为分区(partition)操作;
此时数组被划分为小于基数p、基数p、大于基数p的三部分;
3、递归地(recursive)把小于基数p的子数列和大于基数p的子数列按上面的步骤排序,直到不能再递归。
代码实现的写法也有好多种
代码1
来自维基的,分割写法有点不一样,访问要梯子
选择排序
简单选择排序
常用于取序列中最大最小的几个数时。(如果每次比较都交换,那么就是冒泡;如果每次比较完一个循环再交换,就是简单选择排序。)
1、遍历整个序列,每次将选出来的最小的数放在前面。
2、遍历剩下的序列,依次与哨兵进行比较,选出最小的数。
3、重复第二步,直到只剩下一个数。

写成代码:
1、首先确定循环次数,并且记住当前数字和当前位置。
2、将当前位置后面所有的数与当前数字进行对比,小数赋值给key并记住小数的位置。
3、比对完成后,将最小的值与第一个数的值交换。
4、重复2、3步。
/**
* 选择排序的时间复杂度:简单选择排序的比较次数与序列的初始排序无关。
* 假设待排序的序列有 N 个元素,则比较次数永远都是N (N - 1)/2。
* 而移动次数与序列的初始排序有关。当序列正序时,移动次数最少,为 0,最多会发生 N - 1次交换移动。
* 所以,综上,简单排序的时间复杂度为 O(N^2)。
*
* 空间复杂度为:O(1);与冒泡同理。
*
* 虽然选择排序和冒泡排序的时间复杂度一样,但实际上,选择排序进行的交换操作很少。
*
* 缺点是不稳定:相同的两个数,位置可能会变。
*/
@Test
public void selectSorted() {
int[] a = { 3, 5, 1, 6, 8, 2, 5 };
for (int i = 0; i < a.length - 1; i++) {
int min = i;
for (int j = i + 1; j < a.length; j++) {
if (a[min] > a[j]) {
min = j;
}
}
if (min != i) {
ArrUtil.swap(a, i, min);
}
}
System.out.println(Arrays.toString(a));
}
堆排序
对简单选择排序的优化。
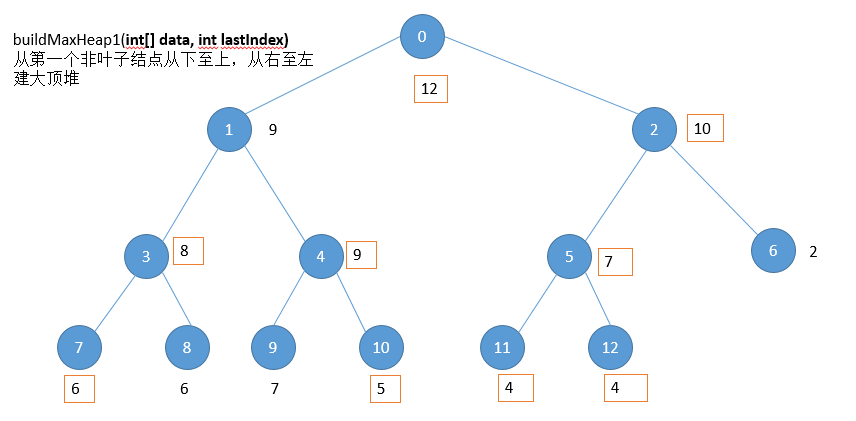
1、将序列构建成大顶堆。
2、将根节点与最后一个节点交换,然后断开最后一个节点。
3、重复第一、二步,直到所有节点断开。
/**
* 堆排序是指利用堆积树(堆)这种数据结构所设计的一种排序算法。一般升序采用大顶堆,降序采用小顶堆
* 把最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。
*
*
* 缺点是不稳定:相同的两个数,位置可能会变。
*/
@Test
public void heapSort() {
int[] a = { 4,9,7,6,5,4,2,8,6,7,9,10,12};
// 循环建堆
for (int i = 0; i < a.length - 1; i++) {
// 建堆
// buildMaxHeap(a, a.length - 1 - i);
buildMaxHeap1(a, a.length - 1 - i);
// 交换堆顶和最后一个元素
ArrUtil.swap(a, 0, a.length - 1 - i);
System.out.println(Arrays.toString(a));
}
}
//从第一个非叶子结点从下至上,从右至左建大顶堆
private void buildMaxHeap1(int[] data, int lastIndex) {
// TODO Auto-generated method stub
//从lastIndex处节点(最后一个节点)的父节点开始
for(int i=(lastIndex-1)/2;i>=0;i--){
//k保存正在判断的节点
int k=i;
//如果当前k节点的子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
if(biggerIndex<lastIndex){
//若果右子节点的值较大
if(data[biggerIndex]<data[biggerIndex+1]){
//biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
//如果k节点的值小于其较大的子节点的值
if(data[k]<data[biggerIndex]){
//交换他们
ArrUtil.swap(data,k,biggerIndex);
//将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值
k=biggerIndex;
}else{
break;
}
}
}
}
插入排序
直接插入排序
把新的数据插入到已经排好的数据列中。
1、将第一个数和第二个数排序,然后构成一个有序序列
2、将第三个数插入进去,构成一个新的有序序列。
3、对第四个数、第五个数……直到最后一个数,重复第二步。
写成代码:
1、首先设定插入次数,即循环次数,for(int i=1;i<length;i++),1个数的那次不用插入。
2、设定插入数和得到已经排好序列的最后一个数的位数。insertNum和j=i-1。
3、从最后一个数开始向前循环,如果插入数小于当前数,就将当前数向后移动一位。
4、将当前数放置到空着的位置,即j+1。
希尔排序
对于直接插入排序问题,数据量巨大时。
1、将数的个数设为n,取奇数k=n/2,将下标差值为k的书分为一组,构成有序序列。
2、再取k=k/2 ,将下标差值为k的书分为一组,构成有序序列。
3、重复第二步,直到k=1执行简单插入排序。
写成代码:
1、首先确定分的组数。
2、然后对组中元素进行插入排序。
3、然后将length/2,重复1,2步,直到length=0为止。
归并排序
速度仅次于快排,内存少的时候使用,可以进行并行计算的时候使用。
1、选择相邻两个数组成一个有序序列。
2、选择相邻的两个有序序列组成一个有序序列。
3、重复第二步,直到全部组成一个有序序列。
分配排序
基数排序
用于大量数,很长的数进行排序时。
1、将所有的数的个位数取出,按照个位数进行排序,构成一个序列。
2、将新构成的所有的数的十位数取出,按照十位数进行排序,构成一个序列。