图像质量评估综述

本文部分内容摘自：https://zhuanlan.zhihu.com/p/32553977

1. 背景介绍

在过去的几十年里，由于质量评估(Quality Assessment，QA)在许多领域有其广泛的实用性，比如图像压缩、视频编解码、视频监控等，并且对高效、可靠质量评估的需求日益增加，所以QA成为一个感兴趣的研究领域，每年都涌现出大量的新的QA算法，有些是扩展已有的算法，也有一些是QA算法的应用。

质量评估可分为图像质量评估（Image Quality Assessment, IQA）和视频质量评估（Video Quality Assessment, VQA），本文主要讨论图像质量评估。IQA从方法上可分为主观评估和客观评估。主观评估就是从人的主观感知来评价图像的质量，首先给出原始参考图像和失真图像，让标注者给失真图像评分，一般采用平均主观得分（Mean Opinion Score, MOS）或平均主观得分差异（Differential Mean Opinion Score, DMOS）表示。客观评估使用数学模型给出量化值，可以使用图像处理技术生成一批失真图像，操作简单，已经成为IQA研究的重点。图像质量评估算法的目标是自动评估与人的主观质量判断相一致的客观图像质量。然而，主观评估费时费力，在实际应用中不可行，并且主观实验受观看距离、显示设备、照明条件、观测者的视觉能力、情绪等诸多因素影响。 因此，有必要设计出能够自动精确的预测主观质量的数学模型。

IQA按照原始参考图像提供信息的多少一般分成3类：全参考(Full Reference-IQA, FR-IQA)、半参考(Reduced Reference-IQA, RR-IQA)和无参考(No Reference-IQA, NR-IQA), 无参考也叫盲参考(Blind IQA, BIQA)。FR-IQA同时有原始(无失真、参考)图像和失真图像,难度较低，核心是对比两幅图像的信息量或特征相似度，是研究比较成熟的方向。NR-IQA只有失真图像，难度较高，是近些年的研究热点，也是IQA中最有挑战的问题。RR-IQA只有原始图像的部分信息或从参考图像中提取的部分特征，此类方法介于FR-IQA和NR-IQA之间，且任何FR-IQA和NR-IQA方法经过适当加工都可以转换成RR-IQA方法。进一步，NR-IQA类算法还可以细分成两类，一类研究特定类型的图像质量，比如估计模糊、块效应、噪声的严重程度，另一类估计非特定类型的图像质量，也就是一个通用的失真评估。一般在实际应用中无法提供参考图像，所以NR-IQA最有实用价值，也有着广泛的应用，使用起来也非常方便，同时，由于图像内容的千变万化并且无参考，也使得NR-IQA成为较难的研究对象。

2. 数据集

要想公正的比较各个IQA算法的性能，有必要建立一个具有各种内容和失真的图像数据集。图像质量评估的数据集也很多，如表1。具有广泛认可的数据集有：LIVE，TID2008，TID2013，CSIQ，IVC和Toyama。给定这些数据集，然后就可以计算平均主观评分和客观模型预测值之间的差异和相关性。 更高的相关性表明更好的模型性能。

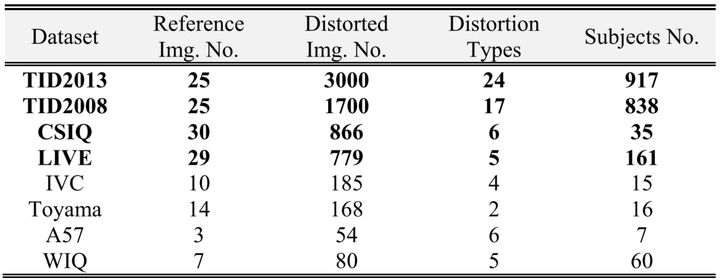
表1：IQA 公开数据集[9]

3. 评估方法

上面简单介绍了IQA的背景知识和数据集，下面是本文的重点，主要介绍IQA的评估指标，使用一些传统算法和深度学习算法解决IQA问题。

3.1 评估指标

衡量图像质量评估结果的指标有很多，每种指标都有自己的特点，通常比较模型客观值与观测的主观值之间的差异和相关性。常见的2种评估指标是线性相关系数（Linear Correlation Coefficient, LCC）和Spearman秩相关系数（Spearman's Rank Order Correlation Coefficient, SROCC）。LCC也叫Pearson相关系数（PLCC），描述了主、客观评估之间的线性相关性，定义如下：

其中  表示失真图像数， 、 分别表示第  幅图像真实值和测试分数， 、 分别表示真实平均值和预测平均值。

SROCC衡量算法预测的单调性，计算公式为：

其中  、  分别表示 、  在真实值和预测值序列中的排序位置。

除此之外，还有Kendall秩相关系数（Kendall Rank Order Correlation Coefficient，KROCC）、均方根误差（Root Mean Square Error， RMSE）等评估指标。KROCC的性质和SROCC一样，也衡量了算法预测的单调性。RMSE计算MOS与算法预测值之间的绝对误差，衡量算法预测的准确性。

3.2 传统算法

以下简单介绍使用传统算法评估FR-IQA、RR-IQA和NR-IQA，文中提到的大部分算法可参考网站cvpr16_gmad。

3.2.1 FR-IQA

对于FR-IQA的研究越来越成熟，出现了很多有影响力的算法，主要是传统算法。比如峰值信噪比（Peak Signal to Noise Ratio, PSNR）通常用来评价一幅图像压缩后和原图像相比质量的好坏，PSNR越高，压缩后失真越小，可以借助均方误差(Mean Square Error， MSE)来计算，计算公式为: 

其中  、 表示两个  的单色图像。  表示图像点颜色的最大值，如果每个采样点用 8 位表示，那么就是 255。对于彩色图像来说的定义类似，只是  是所有方差之和除以图像尺寸再除以 3。

PSNR是图像、视频处理领域应用最广的性能量化方法，计算复杂度小，实现速度快，已经应用在视频编码标准H.264、H.265中。尽管PSNR具有上述特点，但是局限性很明显，受像素点的影响比较大，与主观评价一致性比较低，没有考虑人类视觉系统（Human Visual System， HVS）的一些重要的生理、心理、物理学特征。基于HVS，提出了误差灵敏度分析和结构相似度分析（Structural SIMilarity Index, SSIM）[1]的评价方法。结构相似性假定HVS高度适应于从场景中提取结构信息，试图模拟图像的结构信息，实验表明场景中物体的结构与局部亮度和对比度无关，因此，为了提取结构信息，我们应该分离照明效果。后来又发展出多尺度的结构相似性（Multi-Scale Structural SIMilarity Index, MS-SSIM）[1]和信息量加权的结构相似性(Information Content Weighted Structural Similarity Index, IW-SSIM)[13]，在多尺度方法中，将不同分辨率和观察条件下的图像细节结合到质量评估算法中。 VIF[12]算法使用高斯尺度混合（Gaussian Scale Mixtures, GSMs）在小波域对自然图像进行建模，由源模型，失真模型和HVS模型三部分组成。MAD[8]算法假定HVS在判断图像质量时采用不同的策略，即使用局部亮度、对比度掩蔽和空间频率分量的局部统计量的变化来寻找失真。FSIM[1]算法强调人类视觉系统理解图像主要根据图像低级特征，选择相位一致性（Phase Congruency, PC）和图像梯度幅度（Gradient Magnitude, GM）来计算图像质量。后又加入颜色特征并用相位一致性信息做加权平均，发展出FSIMc[1]算法。VSI[15]算法把FSIMc中的相位一致性特征换成了显著图，保留FSIMc中的梯度和颜色信息，提高了效果。GMSD[14]只用梯度作为特征，采用标准差pooling代替以前的均值pooling，达到了较好的效果。总体上来说，FR-IQA算法性能和速度都在提高，准确率也达到了新高度，如下表2：

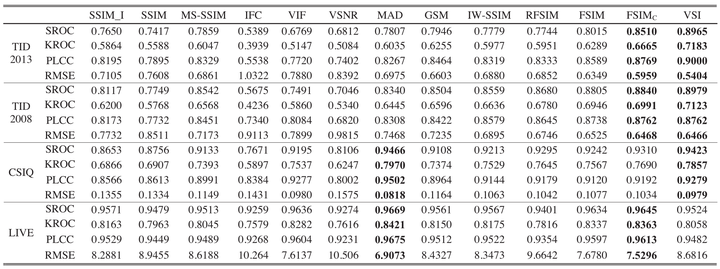
表2：不同FR-IQA算法在四个不同的数据集上的表现对比

3.2.2 RR-IQA

虽然FR-IQA取得了良好的效果，但在许多应用中，参考图像获取不到，只能获取参考图像的一部分信息或间接特征，这便发展出RR-IQA。 RR-IQA方法为参考图像无法完全访问的情况提供了解决方案。 这种类型的方法通常先从参考图像提取最小参数集，然后结合失真图一起来估计质量。RR-IQA研究中的一个重要问题是如何确定IQA任务的有效参数。Maalouf et al等人[10]提出了基于群变换的RR算法， 给定参考图像及其失真版本，将图像组应用于两个图像以便提取图像的纹理和梯度信息， 然后将该信息通过CSF滤波和阈值处理以获得灵敏度系数，最后通过将失真图像的灵敏度系数与参考图像的灵敏度系数进行比较来估计图像质量。Guanawan等人[6]提出了基于局部谐波分析对阻塞或模糊降级的图像进行操作的RR-IQA算法，从边缘检测图像来计算局部谐波幅度信息，然后将该信息与失真图像一起用于估计图像质量。还有其他的基于自然场景统计（Natural Scene Statistics, NSS）的RR-IQA方法，一般的RR-IQA系统见下图：

3.2.3 NR-IQA

现实场景中，人们在没有参考图像的情况下能够无差错地判断失真图像的质量，但从计算机的角度来看，这项任务是相当具有挑战性的。 NR-IQA算法试图不用参考图像来评估图像质量。

绝大多数NR-IQA算法试图检测特定类型的失真，如模糊，块效应，各种形式的噪声等。 例如，用于锐度、模糊度估计的算法已被证明对于模糊图像的NR-IQA表现良好。 NR-IQA方法可以评价图像的模糊度，有基于边缘分析的方法，如使用Sobel、Canny提取图像边缘。有基于变换域的方法，如使用DCT、DWT进行模糊评价。有基于像素统计信息的方法，如统计图像协方差矩阵的最大的前几个特征值的迹作为图像锐度的估计。NR-IQA方法可以估计噪声，有基于滤波的方法、基于小波变换和其他一些变换域的方法。 NR-IQA方法可以评估块效应，有基于块边界和变换域的方法。NR-IQA方法还可以评估JPEG和JPEG2000的压缩失真。

还有一些基于通用类型的NR-IQA算法，这些算法不检测特定类型的失真，他们通常将IQA问题转化成一个分类或回归问题，其中分类、回归是使用特定的特征进行训练的。 相关的特征要么使用自然场景统计提取，要么通过机器学习和深度学习发现。NR-IQA使用自然场景统计的一个主要思想是，自然图像表现出一定的统计规律，可以在失真的情况下进行评估。 我们可以通过提取特征来估计质量，这些特征指示这些统计数据在失真图像中的偏离程度,比如BLINDS-II[1]，这些方法速度通常非常慢，因为使用了计算耗时的图像转换。有基于SVM的方法，这类方法先提取图像空间域或变换域特征, 基于已有的数据训练支持向量回归分析模型（Support Vector Regression, SVR），或者对失真图像使用SVM+SVR模型，代表算法有BIQI[1]，DIIVINE[1]，BRISQUE[1]等。或者使用概率模型的方法，比如BLIINDS[11]，NIQE[1]。或者基于码本的方法，比如CORNIA[1]。并且 CORNIA证明，可以直接从原始图像像素学习判别图像特征，而不使用手工提取特征。

3.3 深度学习算法

最近几年，深度学习已经引起了研究者们的关注，并在各计算机视觉任务上取得了巨大的成功。 具体而言，CNN已经在许多标准的对象识别基准上表现出了优越的性能。 CNN的优势之一是可以直接将原始图像作为输入，并将特征学习融入到训练过程中。 CNN具有深层次的结构，可以有效地学习复杂的映射，同时要求最小的领域知识。这里主要介绍使用深度学习训练NR-IQA。

Le Kang等人[7]使用5层CNN准确的预测NR-IQA，网络结构图如下。该方法输入32*32大小的图像块，使用局部归一化、结合全局max pooling、min pooling、Relu非线性激活层，选择SVR损失函数，使用带动量的SGD来训练模型。 在网络结构中，特征学习和回归被整合到一个优化过程中，从而形成一个更有效的估计图像质量的模型。 这种方法在LIVE数据集上表现了当时最好的性能，并且在交叉数据集实验中显示了出色的泛化能力。文章最后还做了图像局部失真的实验，证明了CNN的局部质量估计能力。

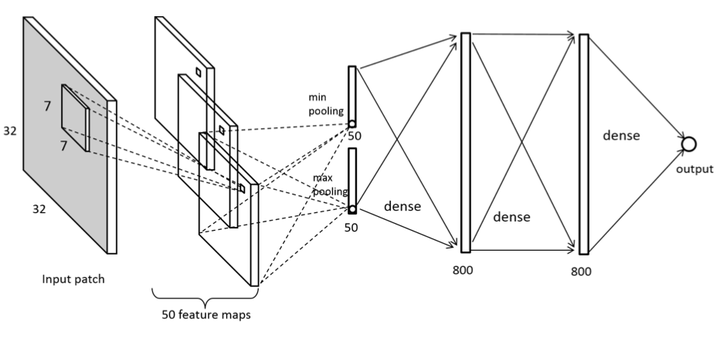
图2：Le Kang等人使用的网络结构

Weilong Hou等也采用深度学习算法进行图像质量评价。使用BIQA框架，综合图像代表，NSS特征，混合特征，分类，后验概率计算等功能为一体，由3级小波变换细节特征为输入，训练过程先采用受限波尔兹曼机RBM进行层间学习，再通过反向传播算法进行微调，最后将预测结果分为5个等级。这个新的基于分类框架比回归框架更加自然，对小训练集更加稳定，通过实验证明模型更加的高效和鲁棒。

Ke Gu等人[5]介绍了一种新的基于深度学习的图像质量指数（Deep learning based Image Quality Index， DIQI）来评估无参考图像质量。首先把RGB图像转换到YIQ颜色空间，从中提取3000个特征，然后使用L-BFGS算法训练一个稀疏的自动编码器，输入数据是s×3000的矩阵，s表示训练样本的个数，设计一个3层的DNN，使用刚才训练的自动编码器初始化DNN，然后使用线性函数计算输出，最后根据损失函数使用反向传播算法微调DNN每层的权重。实验结果表明DIQI的有效性，并且对比经典的FR-IQA、RR-IQA算法，DNN是IQA研究中一个有前景的方向。

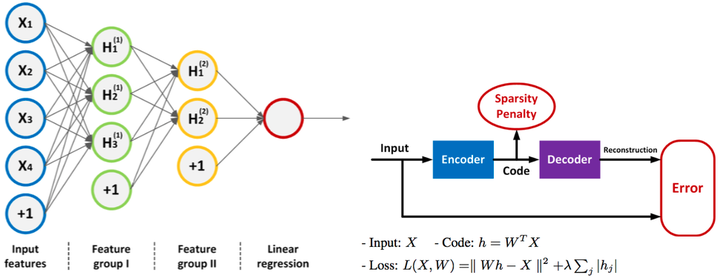
图3：DIQI结构和稀疏表示

Sebastian Bosse等人[4], 设计了一个端到端的深度神经网络。作者修改了VGG网络，新网络包含10个卷积层、5个pooling层来提取特征，2个fc层做回归，将大图片分成多个小块作为输入。然后NR-IQA与FR-IQA共用网络，可以学习出局部权重和局部质量，计算MAE损失进行端到端的训练。作者对比了三种特征向量的融合、空间pooling和权重估计，最后  和平均权重效果最好。只使用NR-IQA分支就可以预测NR-IQA，网络设计比较灵活。实验评估了一些有代表性的公开数据集，都表现出了优越的性能，通过跨数据集的测试表明该算法有很好的泛化能力。

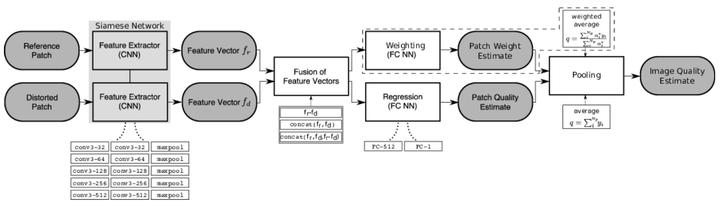
图4：Sebastian Bosse等人使用的网络结构

Simone Bianco等人[3]使用了DeepBIQ模型，DeepBIQ通过将原始图像的多个子区域上预测的分数进行平均来估计图像质量。输入图像块，加载预训练模型微调CNN，输出SVR来计算每个图像块的分数。作者评估了几种效果：1）使用不同的预训练模型，2）使用大量的图像块而不是整个图像训练，同时使用不同的特征和结果融合策略，3）由于图片数据量少，固定网络全连接前的权值，使用NR-IQA数据微调网络。测试图像质量挑战数据集的结果表明，DeepBIQ取得了几乎0.91的LCC。 此外，在许多情况下，DeepBIQ的质量分数预测更接近平均观察者的分数。

图5：DeepBIQ 特征的不同融合方式

Xialei Liu等人[2]提出RankIQA模型来评估无参考图像的质量。之前的模型主要都是从提取特征和网络方面做改进，并没有考虑数据集图像少的问题。而RankIQA正是从数据预处理出发，取得了NR-IQA最好效果。 为了解决IQA数据集不足的问题，通过已知质量的图片使用图像处理变换生成不同级别不同类型的排序的失真图像。这些排序的图像集是自动生成的，而不用人工标注。这样就得到一个大数据集，然后就可以选择一个更宽更深的网络来训练。作者首先选择Siamese网络学习出生成数据排序关系的表示特征，然后将训练好的Siamese网络中表示的知识迁移到传统的CNN中，从而估算出单个图像的绝对图像质量。作者还改进了一个比传统Siamese网络更高效的反向传播算法：以前Siamese网络使用成对的样本训练网络，这样有大量样本有重复计算，现在所有样本只前向传播一次，统计出loss，然后计算梯度进行反向传播，这样得到更快的训练速度和更低的损失。作者实验了三个从浅到深的网络：Shallow，Alexnet，VGG16。Shallow包含4个卷积层和一个fc层，最后VGG16的结果最好。我们还可以训练测试一些更深的网络或者设计一些新网络。作者测试TID2013表明，RankIQA超过state-of-the-art 5％,并且在LIVE测试中，RankIQA优于现有的NR-IQA技术，甚至超越了FR-IQA方法的最新技术，从而无需参考图像就可以推断IQA。

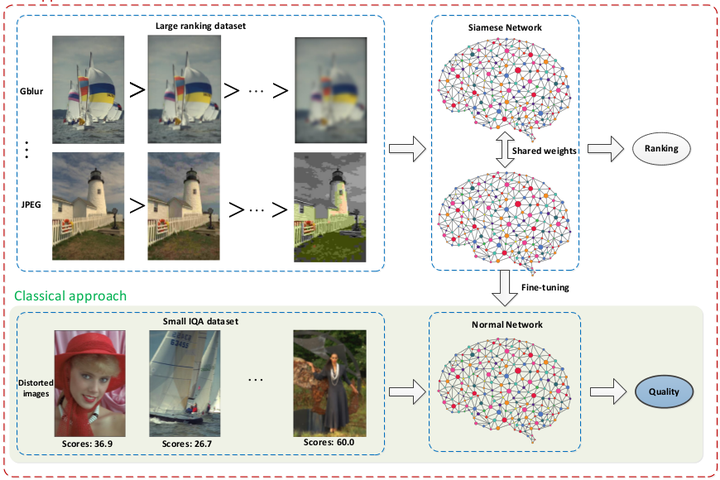图6：RankIQA网络结构

 

3.4 实验结果

在表3中, 统计了一些FR-IQA算法和NR-IQA算法在LIVE数据集上的表现，到目前为止结果最好是RankIQA，RankIQA在NR-IQA上的评估指标甚至超过了FR-IQA。

表 3: 各算法在 LIVE 数据集上的 LCC 和 SROCC 表现

根据RankIQA的主页https://xialeiliu.github.io/RankIQA/提供的文档和源码，首先生成一批排序的失真图像，使用脚本准备好训练、测试集，然后使用网络进行训练。训练模型分为2个阶段，第一阶段使用Siamese网络通过排序图像学习出图像的表示特征，第二阶段使用第一阶段训练好的模型微调自己的IQA数据。我使用自己的数据集：训练集7.5W张，测试集6500，分别微调出了回归和分类模型，微调时使用较小的学习率，回归结果见表4，后使用TID2013+FT模型微调出分类的准确率为 。与公开数据集上的LCC和SROCC差别都比较大，可能原因是自己数据的主观性比较强，与公开数据集存在分布差异。

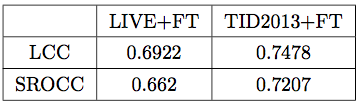
表4: 训练测试自己数据的表现

 

4 总结

从NR-IQA的发展来看，经历了先前针对特定失真类型到基于规则判断的方法后，逐渐到提取复杂特征、基于机器学习的方向发展，直到现在使用深度学习的方法，NR-IQA取得了较好的结果。深度学习具有复杂的网络结构和很好的非线性映射能力，可以端到端的完成特征提取和识别，从实验结果来看，性能超过其他机器学习的方法，在IQA中发挥了重要的作用。但其局限性是设计网络和训练网络都需要一定的技巧，另外训练需要大量的数据，数据量少容易产生过拟合。各个IQA算法也有其局限性，目前还没有客观评价视频编码的算法，虽然PSNR已经应用在视频编码标准中，但是实验证明PSNR和SSIM等算法并不能客观的评价图像质量，如图7，圆外6幅图像MAE相同，即PSNR相同，可是主观观测差别很大，图中SSIM不同，貌似SSIM效果好点，但是有论文证明SSIM并不比PSNR优秀。PSNR范围[0，100]，SSIM的范围[0,1]，他们也没有准确的对应关系。也还没有客观评价与主观评价一致性高的算法，如图8，主观与客观呈现非线性的关系。目前各IQA算法主要评估图片质量都是单一的质量值，并不能反应综合图像质量情况，在各个数据集上SRCC高并不意味着总体上SRCC高。IQA算法对数据集依赖严重，现实中自然图片千变万化，包含多重失真，比公开数据集更复杂，仅靠提升LCC和SROCC是远远不够的。所以现有的IQA算法只能解决一部分问题，如果投入使用还需继续探索。

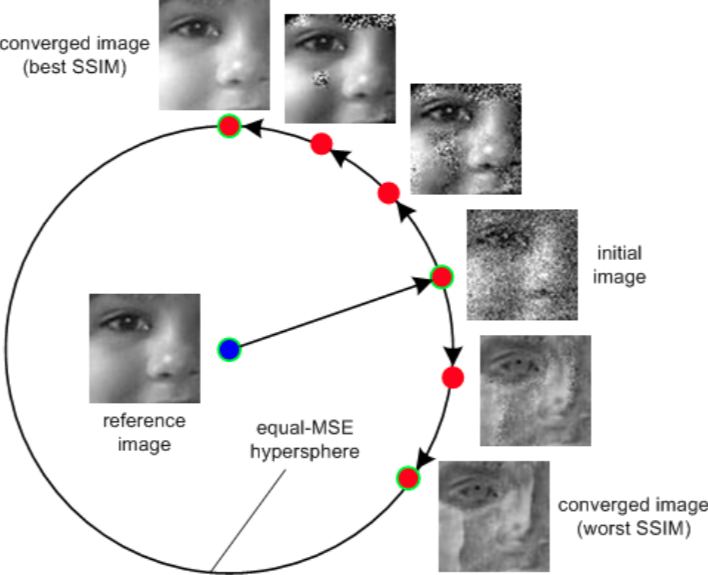图7: 圆内是原始图像，圆外是 6 幅加入不同失真图像，它们 PSNR 相同，SSIM 不同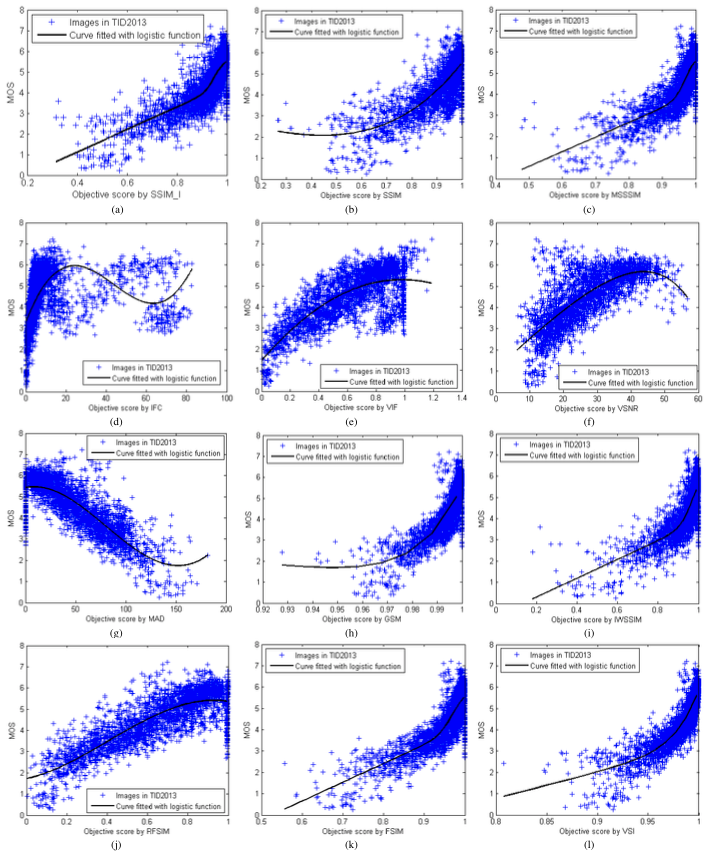

图8: 主观平均得分与模型预测得分的非线性关系

参考文献

[1] Algorithm Reference. https://ece.uwaterloo.ca/~zduanmu/cvpr16_gmad.

[2] RankIQA: Learning from Rankings for No-reference Image Quality Assessment. https://xialeiliu.github.io/RankIQA.

[3] S. Bianco, L. Celona, P. Napoletano, and R. Schettini. On the use of deep learning for blind image quality assessment. arXiv preprint arXiv:1602.05531,  2016.

[4] S. Bosse, D. Maniry, K.-R. Müller, T. Wiegand, and W. Samek. Deep neural networks for no-reference and full-reference image quality assessment. IEEE Transactions on Image Processing, 27(1):206–219, 2018.

[5] K. Gu, G. Zhai, X. Yang, and W. Zhang. Deep learning network for blind image quality assessment. In Image Processing (ICIP), 2014 IEEE International Conference on, pages 511–515. IEEE, 2014.

[6] I. P. Gunawan and M. Ghanbari. Reduced reference picture quality estimation by using local harmonic amplitude information. In London Communications Symposium, volume 2003, pages 353–358, 2003.

[7] L. Kang, P. Ye, Y. Li, and D. Doermann. Convolutional neural networks for no-reference image quality assessment. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1733–1740, 2014.

[8] E. C. Larson and D. M. Chandler. Most apparent distortion: full-reference image quality assessment and the role of strategy. Journal of Electronic Imaging, 19(1):011006–011006, 2010.

[9] 图像质量评价怎么了 – 全参考方法整理与实用性探讨. https://zhuanlan.zhihu.com/p/24804170.

[10] A. Maalouf, M.-C. Larabi, and C. Fernandez-Maloigne. A grouplet-based reduced reference image quality assessment. In Quality of Multimedia Experience, 2009. QoMEx 2009. International Workshop on, pages 59–63. IEEE, 2009.

[11] M. A. Saad, A. C. Bovik, and C. Charrier. A dct statistics-based blind image quality index. IEEE Signal Processing Letters, 17(6):583–586, 2010.

[12] H. R. Sheikh and A. C. Bovik. Image information and visual quality. IEEE Transactions on image processing, 15(2):430–444, 2006.

[13] Z. Wang and Q. Li. Information content weighting for perceptual image quality assessment. IEEE Transactions on Image Processing, 20(5):1185–1198, 2011.

[14] W. Xue, L. Zhang, X. Mou, and A. C. Bovik. Gradient magnitude similarity deviation: A highly e cient perceptual image quality index. IEEE Transactions on Image Processing, 23(2):684–695, 2014.

[15] L. Zhang, Y. Shen, and H. Li. Vsi: A visual saliency-induced index for perceptual image quality assessment. IEEE Transactions on Image Processing, 23(10):4270–4281, 2014.

[16] 视频/图像质量评价综述(一)(二)(三): https://zhuanlan.zhihu.com/p/54539091