1.单一神经元
神经网络是由许许多多的单一神经元构成的,那每一个神经元的实质是什么呢?神经元就干一件事情,叫做非线性变换。如下图所示:
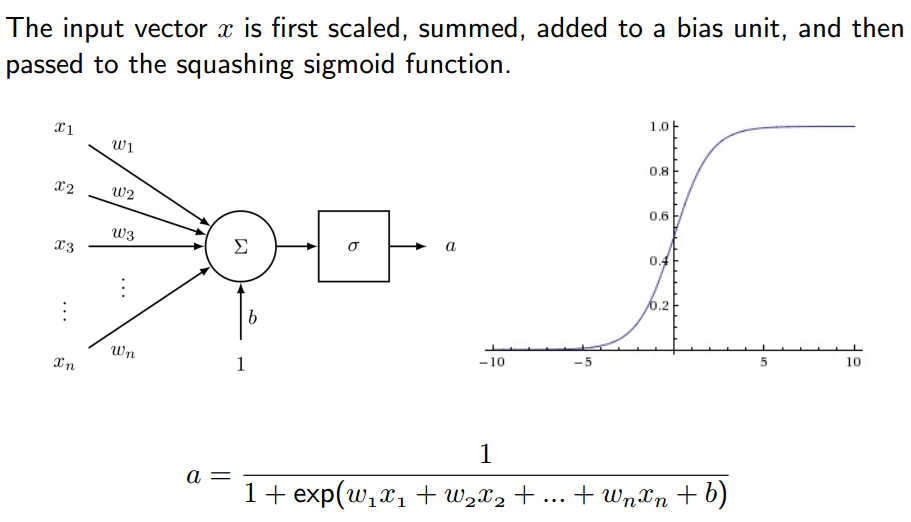
2.神经网络
sigmod激活函数的作用是什么呢?它把一个数从负无穷到正无穷映射为0到1的部分,它只干这么一件事。那什么是神经网络呢?神经元是一个函数吧,那么神经网络是一个超级超级复杂的复合函数。
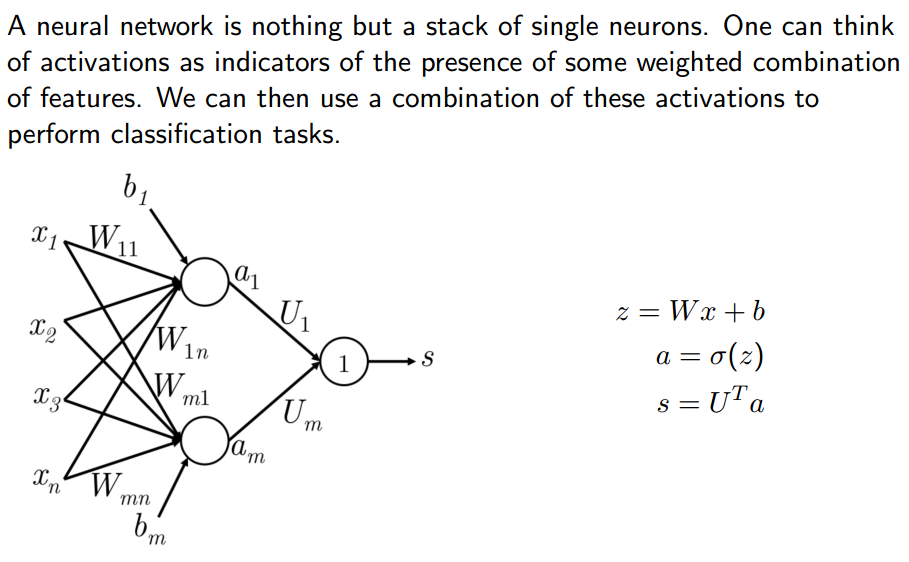
上图中的神经网络实际上与线性分类器如出一辙。你看看啊,上图中有三层网络,每两层之间有权重,这些权重相当于线性分类器中的W矩阵。换句话说,这个神经网络实际上是由两个线性分类器构成的,只不过这里的分类器输出还要做一个非线性变换,当然了,靠近输出的那一层没有做非线性变换。
上图中这里的z是非线性变换之前的结果,而a(activation)是经过非线性变换之后的结果.
3.目标函数

这里的Sc是分类错误的分数,S是分类正确的分数,Xc是输出错误的对应的输入,X是输出正确的对应的输入。Δ的作用是用来增强自信心的,通常取为1.
4.反向传播算法
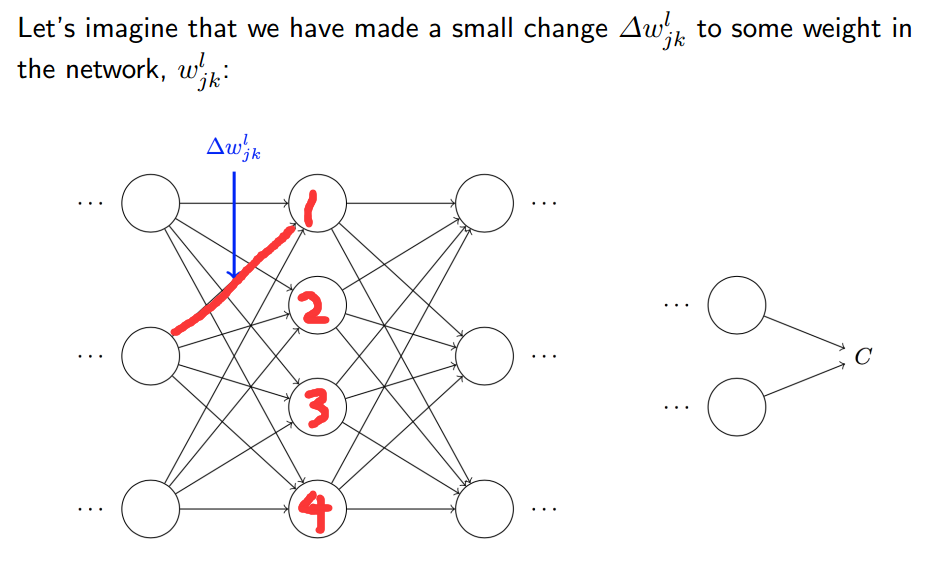
如上图所示,Wjkl 这里的L代表第几层,j代表后边那一层的第j个节点,k代表前边那一层的第K个节点。如果改变图中红色线的权重,那1号神经元的输出结果会受影响,而2,3,4号神经元的输出结果不会受影响。那第三层的神经元都会受变化,因为第二层的第一个神经元受变化了,它跟后边的神经元都连接了。
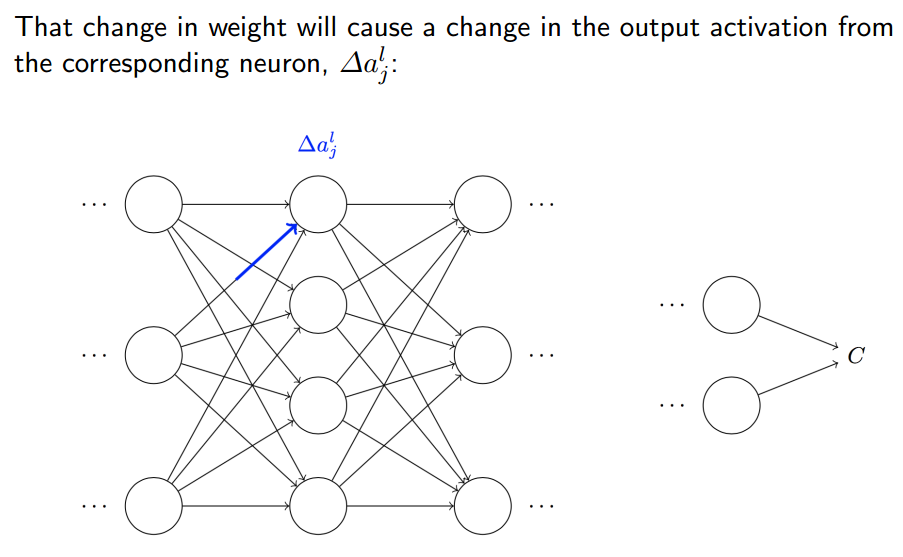
如上图所示,第二层第一个神经元的受到的变化为ΔajL,它一受变化,最终会导致他后边的所有神经元都要受变化,最终会导致损失函数受变化。
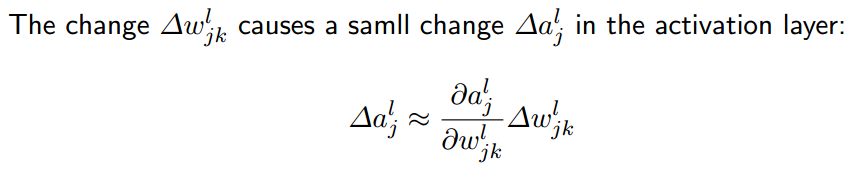
那么第二层第一个神经元受的变化为多少呢?可用上图中的公式计算,可类比为一次函数求变化。求导相当与求斜率,如下图所示:
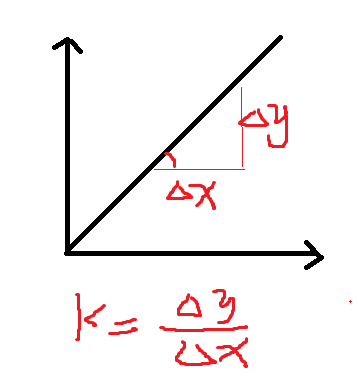
接下来,以此类推,求下一层的变化情况,如下图所示:

直到最后一层,导致损失函数的变化:

因为可能改变的不止一个权重,如果有多个权重发生了改变,如上图所示,用累加求和的办法求出最后损失函数的变化就可以了。
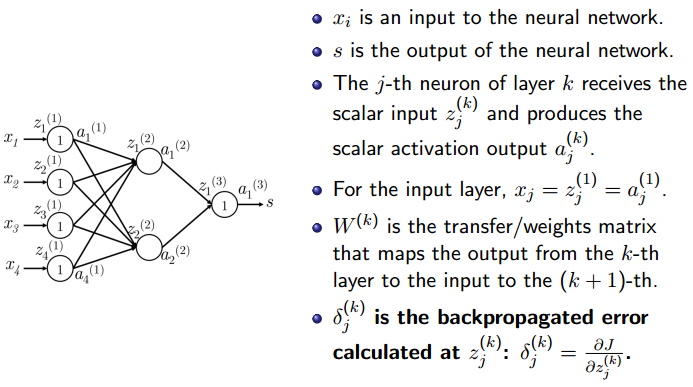
上图中,最后一项,δjk是损失函数对第K层第j个神经元的输入求导。为什么要定义这个呢?这是因为后边的反向传播算法要用到。