题目链接:
https://codeforces.com/contest/1152/problem/D
题意:
给出一个$n$,然后在匹配树上染色边,每个结点的所有相邻边只能被染色一次。
问,这颗树上最多染色多少边。
匹配树,就是深度为$2n$的树,每个节点都是一个字符串,只包含$(,)$,以长度为$2n$的合法匹配字符串作为叶子。每个节点的父亲是比自身长度小一的节点。
数据范围:
$1 le n le 1000$
分析:
在百度找了很久都没找到满意的题解,于是看了cf给的官方题解。虽然是全英文,但我居然看明白了!
实现起来不同,但是思路是一样的。
贪心的方法是,先染色叶子和叶子节点的父亲,并且去除它们,再染色叶子和叶子节点的父亲。
定义不平衡度,$($的数量减$)$的数量。
长度为x,不平衡度为y的子树染色方案数相同
例如这些节点$((()),()()(,(())($的子树,染色方案数相同
选择定义$dp[x][y]$,根节点长度为$x$,不平衡度为$y$,的子树的染色方案数
转移方程为
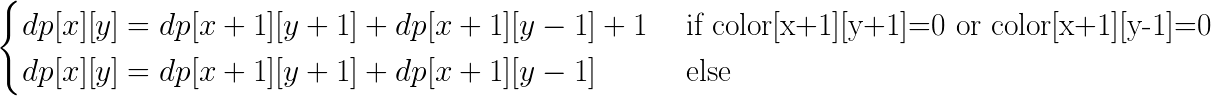
$ans=dp[0][0]$
ac代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e3+10;
const int maxm=1e7+10;
const int mod=1e9+7;
ll dp[2*maxn][2*maxn];
bool color[2*maxn][2*maxn];
int main()
{
int n;
scanf("%d",&n);
for(int i=2*n-1;i>=0;i--)
{
for(int j=0;j<=2*n-i;j++)
{
int flag=0;
if(j-1>=0)
{
dp[i][j]=(dp[i][j]+dp[i+1][j-1])%mod;
if(color[i+1][j-1]==0)flag=1;
}
if(j+1<=2*n-i-1)
{
dp[i][j]=(dp[i][j]+dp[i+1][j+1])%mod;
if(color[i+1][j+1]==0)flag=1;
}
if(flag)color[i][j]=1,dp[i][j]=(dp[i][j]+1)%mod;
}
}
printf("%d
",dp[0][0]);
return 0;
}