20182323 2019-2020-1 《数据结构与面向对象程序设计》实验九报告

学号20182323 2019-2020-1 《数据结构与面向对象程序设计》实验九报告

课程：《程序设计与数据结构》

班级： 1823

姓名： 曹骞

学号： 20182323

实验教师：王志强

实验日期：2019年12月8日

必修/选修： 必修

1.实验内容

1. 初始化：根据屏幕提示（例如：输入1为无向图，输入2为有向图）初始化无向图和有向图（可用邻接矩阵，也可用邻接表），图需要自己定义（顶点个数、边个数，建议先在草稿纸上画出图，然后再输入顶点和边数）（2分）
2. 图的遍历：完成有向图和无向图的遍历（深度和广度优先遍历）（4分）
3. 完成有向图的拓扑排序，并输出拓扑排序序列或者输出该图存在环（3分）
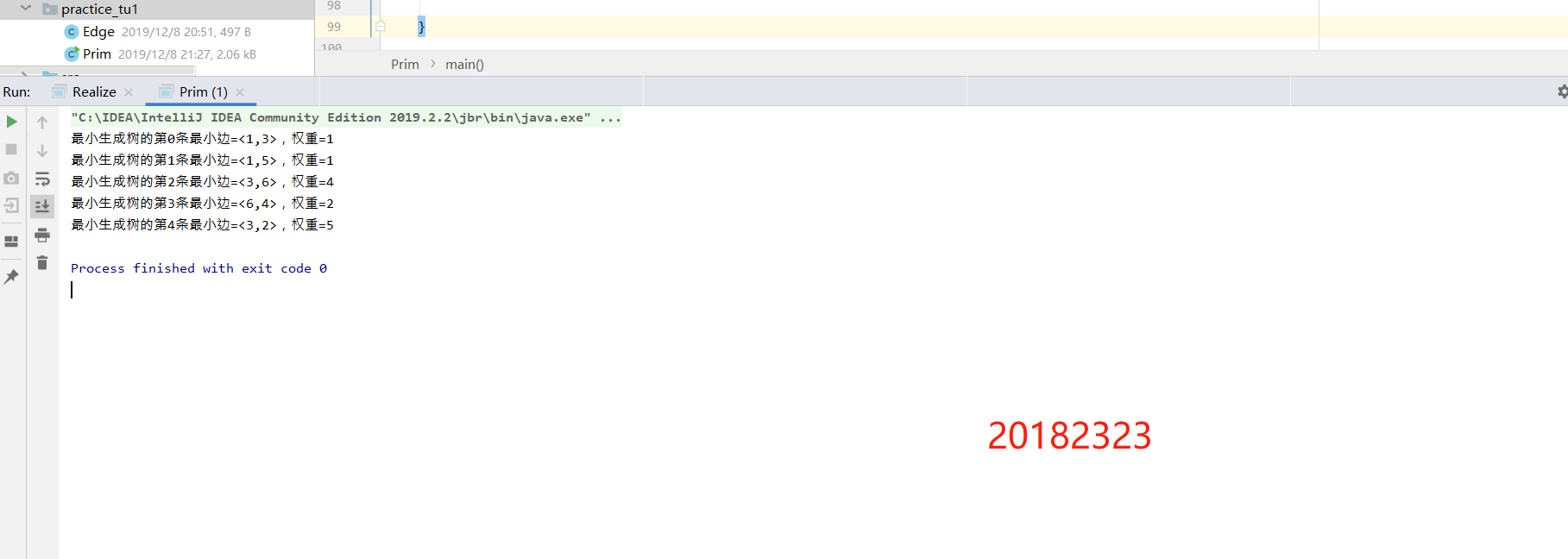
4. 完成无向图的最小生成树（Prim算法或Kruscal算法均可），并输出（3分）
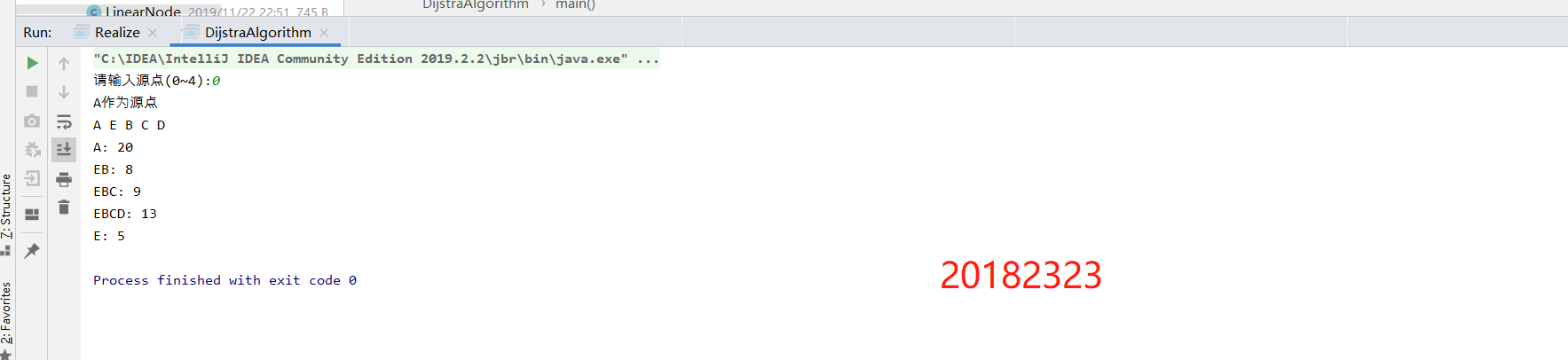
5. 完成有向图的单源最短路径求解（迪杰斯特拉算法）（3分）

2. 实验过程及结果

有向图：

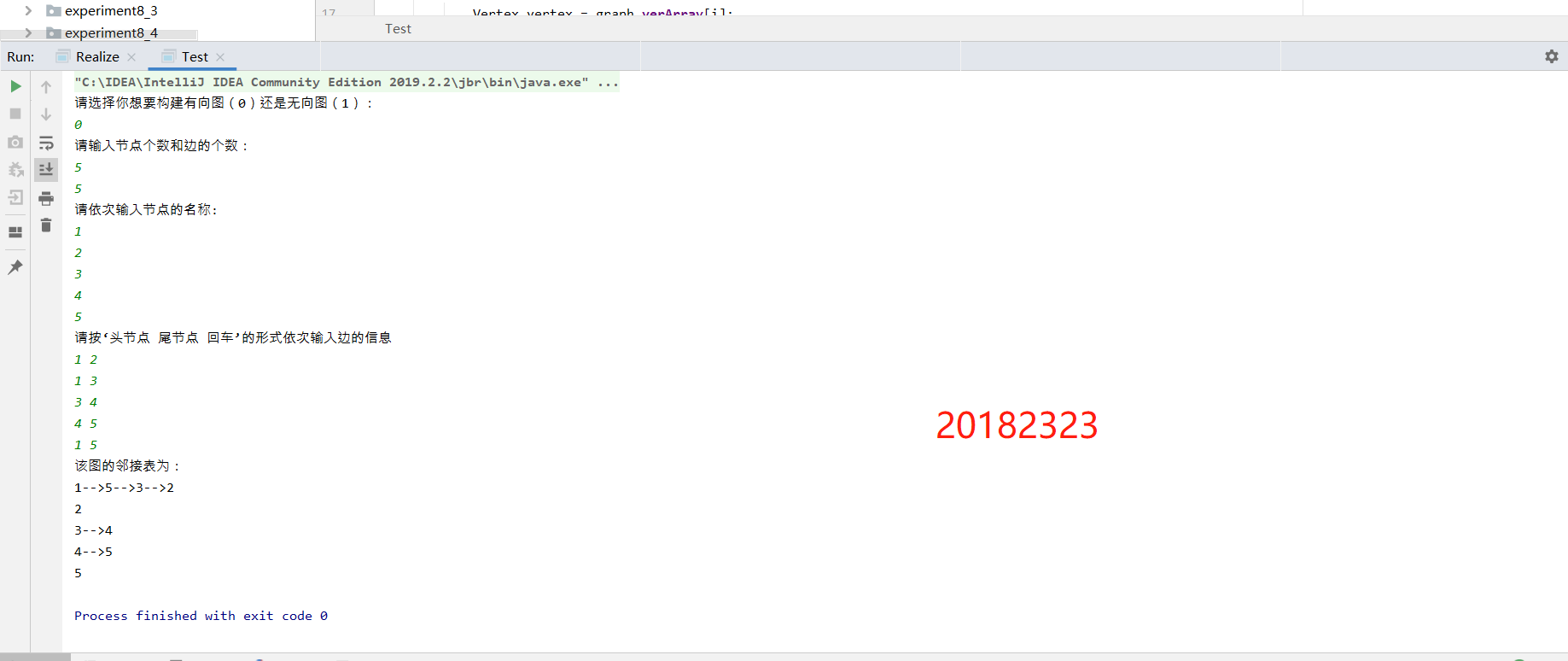
无向图：

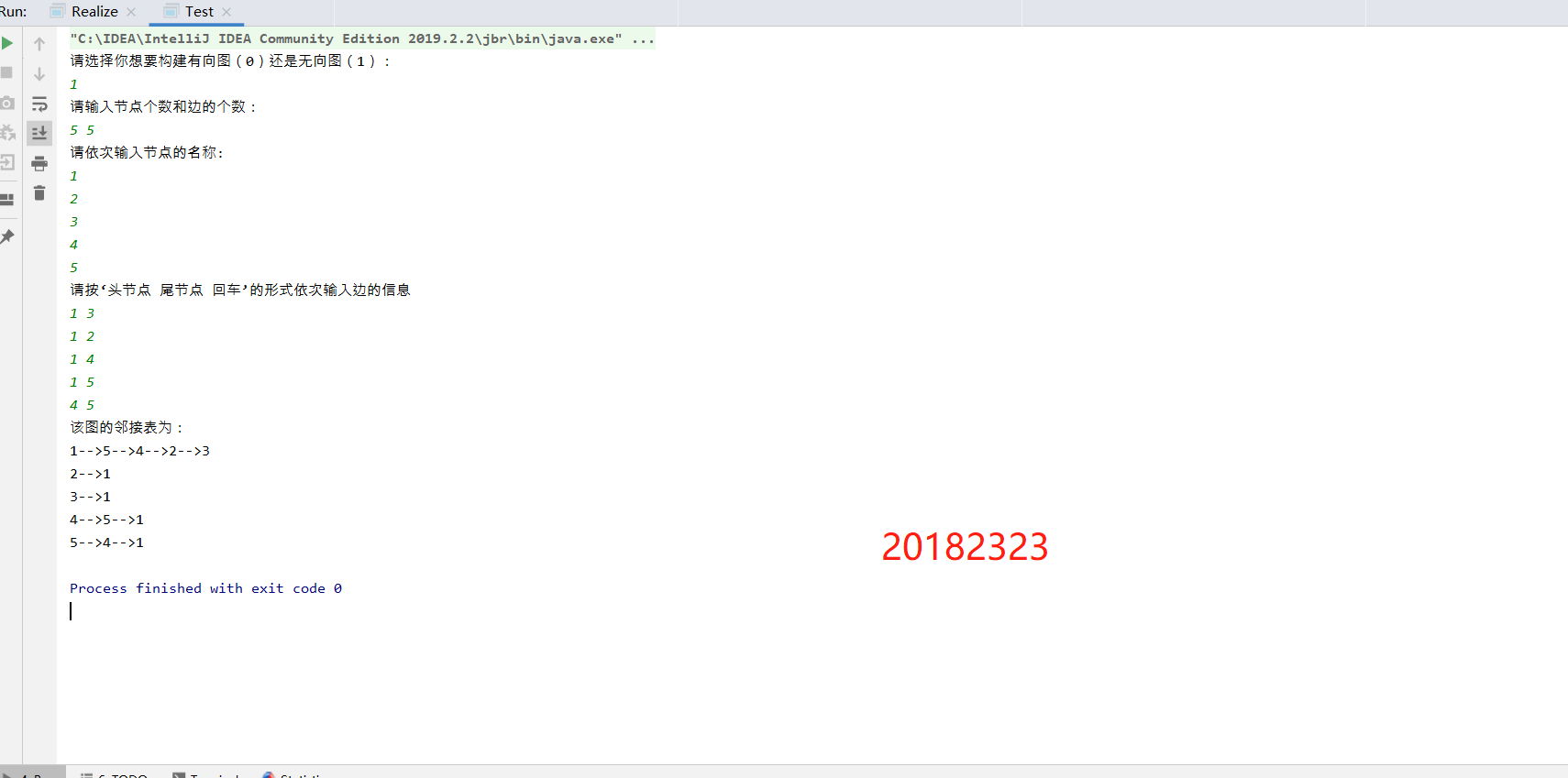
遍历：

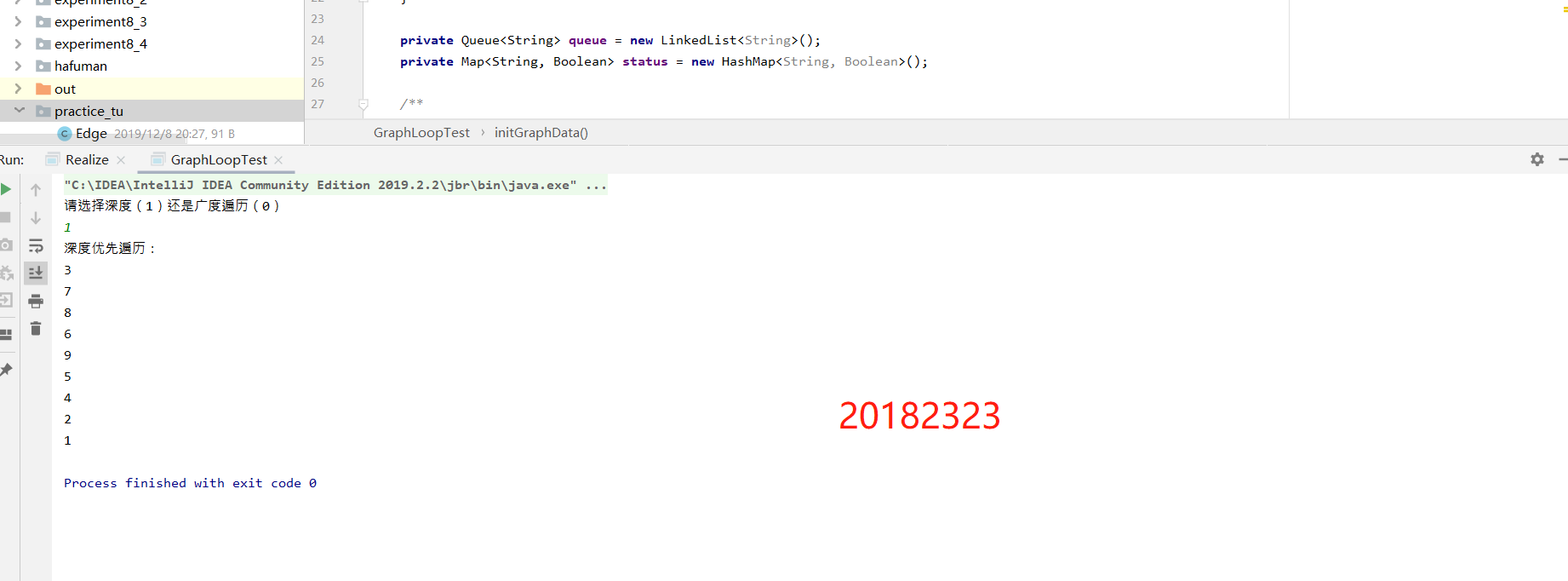
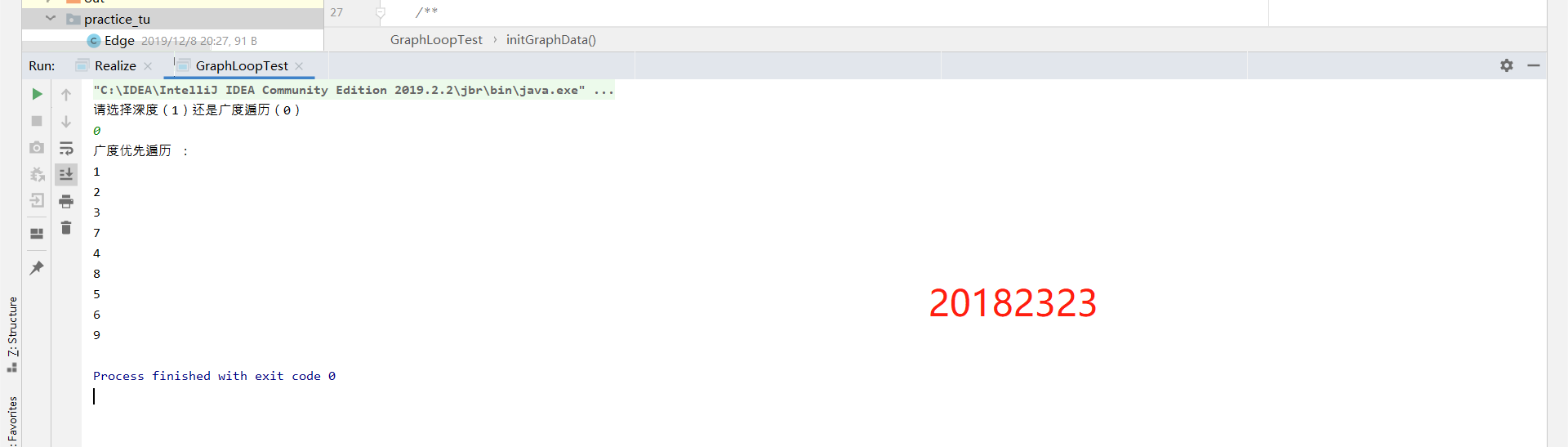
拓扑排序

最小生成树

迪杰斯特拉算法

3. 实验过程中遇到的问题和解决过程

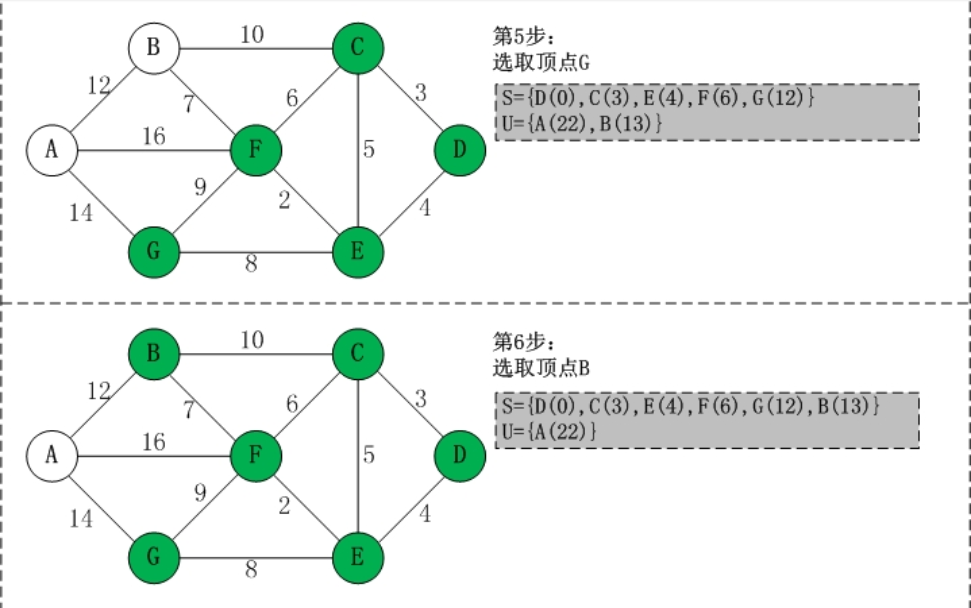
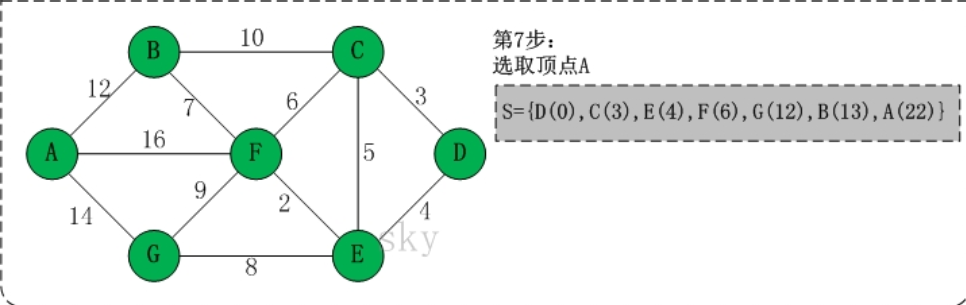
• 问题1：在编写无向网络时需要写一个最便宜路径的问题，当时没有想出来怎么去写，找了一下书上关于这个问题的描述，是关于用Dijkstra算法来解决的。那么，Dijkstra算法具体如何解决问题？

• 问题1解决方案：

  (1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

  (2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

  (3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

  (4) 重复步骤(2)和(3)，直到遍历完所有顶点。
  

其他（感悟、思考等）

这次的倒数第二次实验了，加油！

参考资料

Dijkstra算法之 Java详解