有个学弟说不太明白怎么操作的。
看了看网上的一些讲解,感觉对于初学者来说,确实在理解上存在一些难度,所以就写了个讲解,文辞粗浅,仅资一娱。
基础:会线段数基础的各项操作。
首先,要注意到有两个修改操作,一个区间乘法,一个区间加法,又是加又是乘的,所以一个flag不足以用来标记,要用两个flag。
我假设flag1用来记录乘法,flag2用来记录加法。
在写线段树时紧接着就会发现下面的一个问题:
进行加法和乘法操作时,加乘的顺序不同带来的结果也不相同。
比如:![]() 这两个式子。
这两个式子。
第一个是先加法,后乘法。第二个是先乘法后加法。
他们的结果是截然不同的,在下放标记时,怎样下放呢?
这时就要我们认为的给他规定一个优先级。
一共只有两种可能:加法优先和乘法优先先。
我们先来看乘法优先:
我们在进行式子运算时,可能会有以下两种情况:![]()
因为我们设定的优先级是乘法优先,所以对于第二种情况不会造成干扰,只会对第一种情况有影响。
我们可以很轻易的推出来:(ans+b)*c=ans*c+b*c;
所以我们在遇到乘法标记时,只要把先前存在的加法标记也称一下就好了:
if(tree[now].l==l&&tree[now].r==r){
tree[now].sum=tree[now].sum*k;
tree[now].flag1=tree[now].flag1*k;
tree[now].falg2=tree[now].falg2*k;
return ;
}
加法标记却不影响:
if(tree[now].l==l&&tree[now].r==r){
tree[now].sum+=(tree[now].r-tree[now].l+1)*k;
tree[now].falg2=tree[now].falg2+k;
return ;
}
我们在来看加法标记优先:
我们在进行式子运算时,同样可能会有以下两种情况:![]()
因为我们设定的优先级是乘加法优先,所以对于第一种情况不会造成干扰,只会对第二种情况有影响。
这是,就会发现,恨他对他进行调整,使他满足条件。
所以综上就完成了区间加法和区间乘法的所以操作。
down函数如下:
void down(long long now){
if(tree[now].flag1!=1){
tree[now*2].flag1=tree[now*2].flag1*tree[now].flag1;
tree[now*2].falg2=tree[now*2].falg2*tree[now].flag1;
tree[now*2].sum=tree[now*2].sum*tree[now].flag1;
tree[now*2+1].flag1=tree[now*2+1].flag1*tree[now].flag1;
tree[now*2+1].falg2=tree[now*2+1].falg2*tree[now].flag1;
tree[now*2+1].sum=tree[now*2+1].sum*tree[now].flag1;
tree[now].flag1=1;
}
if(tree[now].falg2){
tree[now*2].falg2=tree[now*2].falg2+tree[now].falg2;
tree[now*2+1].falg2=tree[now*2+1].falg2+tree[now].falg2;
tree[now*2].sum=(tree[now*2].r-tree[now*2].l+1)*tree[now].falg2;
tree[now*2+1].sum=(tree[now*2+1].r-tree[now*2+1].l+1)*tree[now].falg2;
tree[now].falg2=0;
}
}
题目描述
如题,已知一个数列,你需要进行下面三种操作:
1.将某区间每一个数乘上x
2.将某区间每一个数加上x
3.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含三个整数N、M、P,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
输出格式:
输出包含若干行整数,即为所有操作3的结果。
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
(数据已经过加强^_^)
样例说明:
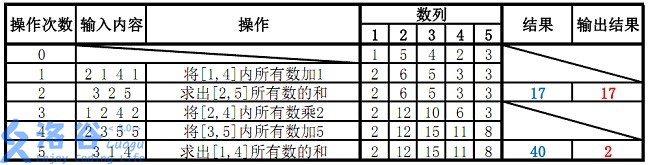
故输出应为17、2(40 mod 38=2)
思路:线段树的区间加法和区间乘法和区间查询。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100001
using namespace std;
struct nond{
long long l,r,sum;
long long flag1,falg2;
}tree[MAXN*4];
long long n,m,p;
void up(long long now){
tree[now].sum=(tree[now*2].sum+tree[now*2+1].sum)%p;
}
void build(long long now,long long l,long long r){
tree[now].l=l;tree[now].r=r;
tree[now].flag1=1;tree[now].falg2=0;
if(tree[now].l==tree[now].r){
scanf("%d",&tree[now].sum);
return ;
}
long long mid=(tree[now].l+tree[now].r)/2;
build(now*2,l,mid);
build(now*2+1,mid+1,r);
up(now);
}
void down(long long now){
if(tree[now].flag1!=1){
tree[now*2].flag1=tree[now*2].flag1*tree[now].flag1%p;
tree[now*2].falg2=tree[now*2].falg2*tree[now].flag1%p;
tree[now*2].sum=tree[now*2].sum*tree[now].flag1%p;
tree[now*2+1].flag1=tree[now*2+1].flag1*tree[now].flag1%p;
tree[now*2+1].falg2=tree[now*2+1].falg2*tree[now].flag1%p;
tree[now*2+1].sum=tree[now*2+1].sum*tree[now].flag1%p;
tree[now].flag1=1;
}
if(tree[now].falg2){
tree[now*2].falg2=(tree[now*2].falg2+tree[now].falg2)%p;
tree[now*2+1].falg2=(tree[now*2+1].falg2+tree[now].falg2)%p;
tree[now*2].sum=(tree[now*2].sum+(tree[now*2].r-tree[now*2].l+1)*tree[now].falg2%p)%p;
tree[now*2+1].sum=(tree[now*2+1].sum+(tree[now*2+1].r-tree[now*2+1].l+1)*tree[now].falg2%p)%p;
tree[now].falg2=0;
}
}
void changechen(long long now,long long l,long long r,long long k){
if(tree[now].l==l&&tree[now].r==r){
tree[now].sum=tree[now].sum*k%p;
tree[now].flag1=tree[now].flag1*k%p;
tree[now].falg2=tree[now].falg2*k%p;
return ;
}
if(tree[now].flag1!=1||tree[now].falg2) down(now);
long long mid=(tree[now].l+tree[now].r)/2;
if(r<=mid) changechen(now*2,l,r,k);
else if(l>mid) changechen(now*2+1,l,r,k);
else{
changechen(now*2,l,mid,k);
changechen(now*2+1,mid+1,r,k);
}
up(now);
}
void changeadd(long long now,long long l,long long r,long long k){
if(tree[now].l==l&&tree[now].r==r){
tree[now].sum=(tree[now].sum+(tree[now].r-tree[now].l+1)*k%p)%p;
tree[now].falg2=(tree[now].falg2+k)%p;
return ;
}
if(tree[now].flag1!=1||tree[now].falg2) down(now);
long long mid=(tree[now].l+tree[now].r)/2;
if(r<=mid) changeadd(now*2,l,r,k);
else if(l>mid) changeadd(now*2+1,l,r,k);
else{
changeadd(now*2,l,mid,k);
changeadd(now*2+1,mid+1,r,k);
}
up(now);
}
long long query(long long now,long long l,long long r){
if(tree[now].l==l&&tree[now].r==r)
return tree[now].sum%p;
if(tree[now].flag1!=1||tree[now].falg2) down(now);
long long mid=(tree[now].l+tree[now].r)/2;
if(r<=mid) return query(now*2,l,r);
else if(l>mid) return query(now*2+1,l,r);
else return (query(now*2,l,mid)+query(now*2+1,mid+1,r))%p;
}
int main(){
scanf("%lld%lld%lld",&n,&m,&p);
build(1,1,n);
for(long long i=1;i<=m;i++){
long long opt,x,y,k;
scanf("%lld%lld%lld",&opt,&x,&y);
if(opt==1){
scanf("%lld",&k);
changechen(1,x,y,k);
}
else if(opt==2){
scanf("%lld",&k);
changeadd(1,x,y,k);
}
else if(opt==3) printf("%lld
",query(1,x,y)%p);
}
}