A. Supermarket
We often go to supermarkets to buy some fruits or vegetables, and on the tag there prints the price for a kilo. But in some supermarkets, when asked how much the items are, the clerk will say that a yuan for bkilos (You don't need to care about what "yuan" is), the same as a / b yuan for a kilo.
Now imagine you'd like to buy m kilos of apples. You've asked n supermarkets and got the prices. Find the minimum cost for those apples.
You can assume that there are enough apples in all supermarkets.
Input
The first line contains two positive integers n and m (1 ≤ n ≤ 5 000, 1 ≤ m ≤ 100), denoting that there are n supermarkets and you want to buy m kilos of apples.
The following n lines describe the information of the supermarkets. Each line contains two positive integersa, b (1 ≤ a, b ≤ 100), denoting that in this supermarket, you are supposed to pay a yuan for b kilos of apples.
Output
The only line, denoting the minimum cost for m kilos of apples. Please make sure that the absolute or relative error between your answer and the correct answer won't exceed 10 - 6.
Formally, let your answer be x, and the jury's answer be y. Your answer is considered correct if 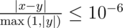 .
.
Examples
input 3 5 1 2 3 4 1 3 output 1.66666667
input 2 1 99 100 98 99 output 0.98989899
Note
In the first sample, you are supposed to buy 5 kilos of apples in supermarket 3. The cost is 5 / 3 yuan.
In the second sample, you are supposed to buy 1 kilo of apples in supermarket 2. The cost is 98 / 99 yuan.
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n; double m,ans=1000000000.0; int main(){ scanf("%d%lf",&n,&m); for(int i=1;i<=n;i++){ double a,b; scanf("%lf%lf",&a,&b); ans=min(ans,m*a/b); } printf("%.8lf",ans); }
B. Perfect Number
We consider a positive integer perfect, if and only if the sum of its digits is exactly 10. Given a positive integer k, your task is to find the k-th smallest perfect positive integer.
Input
A single line with a positive integer k (1 ≤ k ≤ 10 000).
Output
A single number, denoting the k-th smallest perfect integer.
Examples
input 1 output 19
input 2 output 28
Note
The first perfect integer is 19 and the second one is 28.
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,tot; int main(){ scanf("%d",&n); for(long long i=19;i;i+=9){ long long k=i;int sum=0; while(k){ sum+=k%10; k/=10; } if(sum==10) tot++; if(tot==n){ cout<<i;break; } } }
C. Seat Arrangements
Suppose that you are in a campus and have to go for classes day by day. As you may see, when you hurry to a classroom, you surprisingly find that many seats there are already occupied. Today you and your friends went for class, and found out that some of the seats were occupied.
The classroom contains n rows of seats and there are m seats in each row. Then the classroom can be represented as an n × m matrix. The character '.' represents an empty seat, while '*' means that the seat is occupied. You need to find k consecutive empty seats in the same row or column and arrange those seats for you and your friends. Your task is to find the number of ways to arrange the seats. Two ways are considered different if sets of places that students occupy differs.
Input
The first line contains three positive integers n, m, k (1 ≤ n, m, k ≤ 2 000), where n, m represent the sizes of the classroom and k is the number of consecutive seats you need to find.
Each of the next n lines contains m characters '.' or '*'. They form a matrix representing the classroom, '.' denotes an empty seat, and '*' denotes an occupied seat.
Output
A single number, denoting the number of ways to find k empty seats in the same row or column.
Examples
input 2 3 2 **. ... output 3
input 1 2 2 .. output 1
input 3 3 4 .*. *.* .*. output 0
Note
In the first sample, there are three ways to arrange those seats. You can take the following seats for your arrangement.
- (1, 3), (2, 3)
- (2, 2), (2, 3)
- (2, 1), (2, 2)
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n,m,k,ans; int map[2001][2001]; int main(){ scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ char s;cin>>s; if(s=='*') map[i][j]=1; else map[i][j]=0; } for(int i=1;i<=n;i++){ int sum=0; for(int j=1;j<=m;j++){ if(!map[i][j]) sum++; else{ if(sum>=k) ans+=sum-k+1; sum=0; } } if(sum>=k) ans+=sum-k+1; } for(int j=1;j<=m;j++){ int sum=0; for(int i=1;i<=n;i++){ if(!map[i][j]) sum++; else{ if(sum>=k) ans+=sum-k+1; sum=0; } } if(sum>=k) ans+=sum-k+1; } if(k==1) cout<<ans/2; else cout<<ans; } /* 2 3 1 **. ... 3 3 1 .*. *.* .*. */
D. Substring
You are given a graph with n nodes and m directed edges. One lowercase letter is assigned to each node. We define a path's value as the number of the most frequently occurring letter. For example, if letters on a path are "abaca", then the value of that path is 3. Your task is find a path whose value is the largest.
Input
The first line contains two positive integers n, m (1 ≤ n, m ≤ 300 000), denoting that the graph has n nodes and m directed edges.
The second line contains a string s with only lowercase English letters. The i-th character is the letter assigned to the i-th node.
Then m lines follow. Each line contains two integers x, y (1 ≤ x, y ≤ n), describing a directed edge from x to y. Note that x can be equal to y and there can be multiple edges between x and y. Also the graph can be not connected.
Output
Output a single line with a single integer denoting the largest value. If the value can be arbitrarily large, output -1 instead.
Examples
input 5 4 abaca 1 2 1 3 3 4 4 5 output 3
input 6 6 xzyabc 1 2 3 1 2 3 5 4 4 3 6 4 output -1
input 10 14 xzyzyzyzqx 1 2 2 4 3 5 4 5 2 6 6 8 6 5 2 10 3 9 10 9 4 6 1 10 2 8 3 7 output 4
Note
In the first sample, the path with largest value is 1 → 3 → 4 → 5. The value is 3 because the letter 'a' appears 3 times.
思路:tarjin判环+记忆化搜索处理找最大的。
(木有过样例)
#include<map> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define MAXN 300001 using namespace std; map<int,int>ma[MAXN]; char s[MAXN],s1[MAXN]; int n,m,tot,tot1; int top,tim,sumcol,ans=-1; int to[MAXN],net[MAXN],head[MAXN]; int to1[MAXN],net1[MAXN],head1[MAXN]; int col[MAXN],vis[MAXN],f[MAXN][27],val[MAXN]; int low[MAXN],dfn[MAXN],stack[MAXN],visstack[MAXN]; void add(int u,int v){ to[++tot]=v;net[tot]=head[u];head[u]=tot; } void add1(int u,int v){ to1[++tot1]=v;net1[tot1]=head1[u];head1[u]=tot1; } void tarjin(int now){ low[now]=dfn[now]=++tim; vis[now]=1; stack[++top]=now; visstack[now]=1; for(int i=head[now];i;i=net[i]) if(!vis[to[i]]){ tarjin(to[i]); low[now]=min(low[now],low[to[i]]); } else if(visstack[to[i]]) low[now]=min(low[now],dfn[to[i]]); if(low[now]==dfn[now]){ sumcol++; col[now]=sumcol; while(stack[top]!=now){ col[stack[top]]=sumcol; visstack[stack[top]]=0; top--; } visstack[now]=0; top--; } } int dfs(int now,int c){ if(f[now][c]!=-1) return f[now][c]; int res=0; for(int i=head[now];i;i=net[i]) res=max(res,dfs(to[i],c)); res+=(val[now]==c); f[now][c]=res; return f[now][c]; } int main(){ scanf("%d%d",&n,&m); scanf("%s",s+1); for(int i=1;i<=m;i++){ int a,b; scanf("%d%d",&a,&b); add(a,b); } for(int i=1;i<=n;i++) if(!vis[i]) tarjin(i); memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) if(!vis[col[i]]) vis[col[i]]=1; else{ cout<<"-1";return 0; } for(int i=1;i<=n;i++) for(int j=head[i];j;j=net[j]) if(col[i]!=col[to[j]]) if(ma[col[i]].find(col[to[j]])==ma[col[i]].end()){ ma[col[i]][col[to[j]]]=1; add1(col[i],col[to[j]]); } for(int i=1;i<=n;i++) s1[col[i]]=s[i]; for(int i=1;i<=n;i++) val[i]=s1[i]-'a'; memset(f,-1,sizeof(f)); for(int i=1;i<=n;i++) for(int j=0;j<26;j++) ans=max(ans,dfs(i,j)); cout<<ans; }