题意翻译
题目描述
给你一个整数N。考虑坐标轴上所有可能的部分，在整数点上的端点，坐标在0到N之间，包括它们。 您希望在几个层中绘制这些片段，这样在每个层中这些片段就不会重叠（尽管它们可能会接触到端点）。不能将这些段移动到坐标轴上的另一个位置。 找出给定N必须使用的最低层数。
输入格式：
唯一的输入行包含一个整数N（1<=N<=100）。
输出格式：
输出一个整数为给定的N绘制片段所需的最低层数。 采纳：鲁罗啵天霸
题目描述
You are given an integer NN . Consider all possible segments on the coordinate axis with endpoints at integer points with coordinates between 0 and NN , inclusive; there will be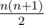 
of them.
You want to draw these segments in several layers so that in each layer the segments don't overlap (they might touch at the endpoints though). You can not move the segments to a different location on the coordinate axis.
Find the minimal number of layers you have to use for the given NN .
输入输出格式
输入格式：
The only input line contains a single integer NN ( 1<=N<=1001<=N<=100 ).
输出格式：
Output a single integer - the minimal number of layers required to draw the segments for the given NN .
输入输出样例
说明
As an example, here are the segments and their optimal arrangement into layers for N=4N=4 .
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int n; int ans[105]; int main(){ cin>>n; ans[1]=1;ans[2]=2;ans[3]=4;ans[4]=6; for(int i=5;i<=100;i++) ans[i]=2*ans[i-1]-2*ans[i-3]+ans[i-4]; cout<<ans[n]<<endl; }