题目背景
滚粗了的HansBug在收拾旧英语书,然而他发现了什么奇妙的东西。
题目描述
udp2.T3如果遇到相同的字符串,输出后面的
蒟蒻HansBug在一本英语书里面找到了一个单词表,包含N个单词(每个单词内包含大小写字母)。现在他想要找出某一段连续的单词内字典序最大的单词。
输入输出格式
输入格式:
第一行包含两个正整数N、M,分别表示单词个数和询问个数。
接下来N行每行包含一个字符串,仅包含大小写字母,长度不超过15,表示一个单词。
再接下来M行每行包含两个整数x、y,表示求从第x到第y个单词中字典序最大的单词。
输出格式:
输出包含M行,每行为一个字符串,分别依次对应前面M个询问的结果。
输入输出样例
输入样例#1:
5 5 absi hansbug lzn kkk yyy 1 5 1 1 1 2 2 3 4 4
输出样例#1:
yyy absi hansbug lzn kkk
说明
样例说明:
第一次操作:在{absi,hansbug,lzn,kkk,yyy}中找出字典序最大的,故为yyy
第二次操作:在{absi}中找出字典序最大的,故为absi
第三次操作:在{absi,hansbug}中找出字典序最大的,故为hansbug
第四次操作:在{hansbug,lzn}中找出字典序最大的,故为lzn
第五次操作:在{kkk}中找出字典序最大的,故为kkk
数据规模:
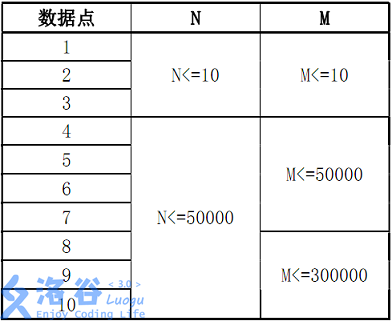
注意事项:1.该题目单词字典序比对过程中大小写不敏感,但是输出必须输出原单词
2.该题目时间限制为0.2s
此题暴力给字符串比较大小是玄学,80~AC
正解:trie树给字符串排序,st表做RMQ
先序遍历就是排序
一堆RE,结果发现len打成n了
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; const int N=50005,L=17; inline int read(){ char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int n,m,l,r; char s[N][20],a[20]; int ch[N*L][27],size=0,val[N*L]; void insert(char s[],int n,int id){ int u=0; for(int i=1;i<=n;i++){ int v=s[i]-'a'; if(!ch[u][v]) ch[u][v]=++size; u=ch[u][v]; } val[u]=id;//printf("ins %d %d ",u,id); } int rank[N],p=0; void dfs(int u){//printf("dfs %d ",u); if(val[u]) rank[val[u]]=++p; for(int i=0;i<26;i++) if(ch[u][i]) dfs(ch[u][i]); } int mx[N][17]; inline int maxs(int i,int j){return rank[i]>rank[j]?i:j;} void initRMQ(){ for(int i=1;i<=n;i++) mx[i][0]=i; for(int j=1;j<=16;j++) for(int i=1;i+(1<<j)-1<=n;i++) mx[i][j]=maxs(mx[i][j-1],mx[i+(1<<(j-1))][j-1]); } inline int query(int l,int r){ int k=log(r-l+1)/log(2); return maxs(mx[l][k],mx[r-(1<<k)+1][k]); } int main(){ n=read();m=read(); for(int i=1;i<=n;i++){ scanf("%s",s[i]+1); int len=strlen(s[i]+1); for(int j=1;j<=len;j++) a[j]=s[i][j]<'a'?s[i][j]+'a'-'A':s[i][j]; insert(a,len,i); } dfs(0);//sort //for(int i=1;i<=n;i++) printf("%d %d ",i,rank[i]); initRMQ(); for(int i=1;i<=m;i++){ l=read();r=read(); printf("%s ",s[query(l,r)]+1); } }