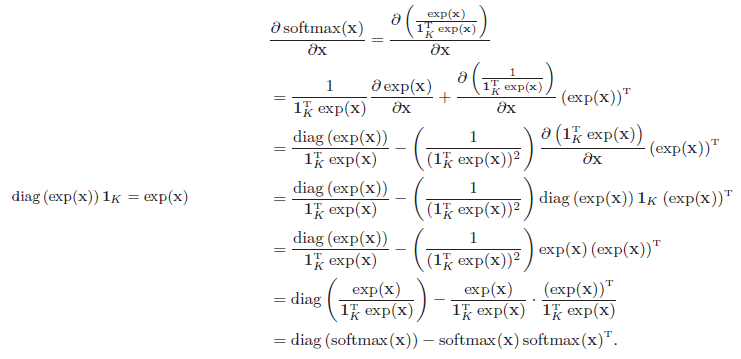导数
对于定义域和值域都是实数域的函数f : R → R,若f(x) 在点x0 的某个邻域Δx 内,极限
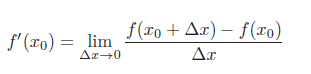
存在,则称函数f(x) 在点x0 处可导,f′(x0) 称为其导数,或导函数,也可以记为![]()
给定一个连续函数,计算其导数的过程称为微分(Differentiation)。微分的逆过程为积分(Integration)。函数f(x) 的积分可以写为
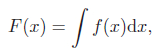
其中F(x) 称为f(x) 的原函数。
若函数f(x) 在其定义域包含的某区间内每一个点都可导,那么也可以说函数f(x) 在这个区间内可导。如果一个函数f(x) 在定义域中的所有点都存在导数,则f(x) 为可微函数(Differentiable Function)。可微函数一定连续,但连续函数不一定可微。例如函数|x| 为连续函数,但在点x = 0 处不可导。
高阶导数
对一个函数的导数继续求导,可以得到高阶导数。函数f(x) 的导数f′(x) 称为一阶导数,f′(x) 的导数称为二阶导数,记为f′′(x) 或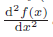
偏导数
对于一个多变量函数f : Rd → R,它的偏导数(Partial Derivative )是关于其中一个变量xi 的导数,而保持其他变量固定,可以记为f′xi (x),∇xif(x),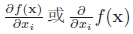
导数法则
加法和乘法法则

链式法则

常见函数的导数
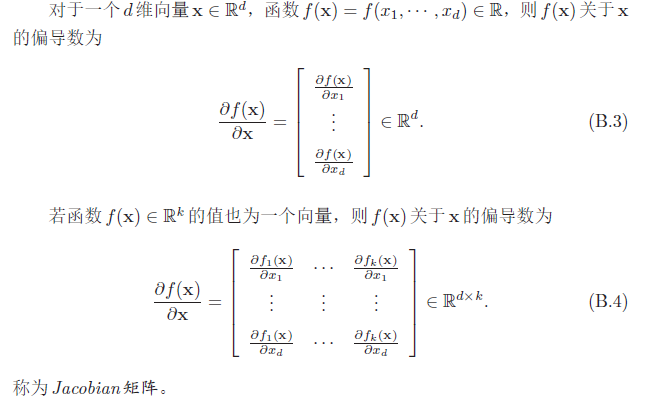
向量函数及其导数
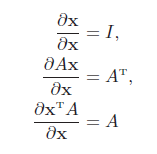
按位计算的向量函数及其导数

Logistic 函数
Logistic 函数是一种常用的S形函数,是比利时数学家Pierre François Verhulst在1844-1845 年研究种群数量的增长模型时提出命名的,最初作为一种生态学模型。
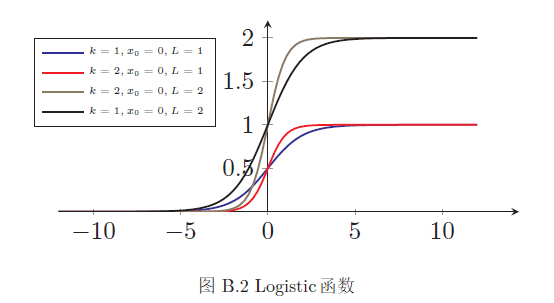
Logistic 函数定义为:
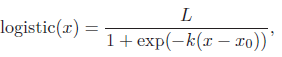
这里exp(·) 函数表示自然对数,x0 是中心点,L是最大值,k 是曲线的倾斜度。图B.2给出了几种不同参数的logistic 函数曲线。当x 趋向于−∞时,logistic(x)接近于0;当x 趋向于+∞时,logistic(x) 接近于L.
当参数为(k = 1, x0 = 0,L = 1) 时,logistic 函数称为标准logistic 函数(sigmoid),记为σ(x)。
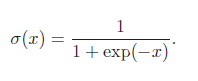
标准logistic 函数在机器学习中使用得非常广泛,经常用来将一个实数空间的数映射到(0, 1) 区间。
标准logistic 函数的导数为
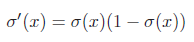
当输入为K 维向量x = [x1, · · · , xK]T 时,其导数为
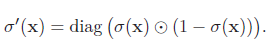
注意:
1. 如果神经网络不加激活函数相当于:y=ax+b,导数为常数
2. sigmoid函数求导出来是一个矩阵,但是因为变量也是一个矩阵,所以可以进行权值更新
softmax 函数
softmax 函数是将多个标量映射为一个概率分布。对于K 个标量x1, · · · , xK,softmax 函数定义为
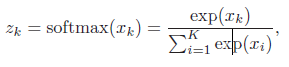
这样,我们可以将K 个变量x1, · · · , xK 转换为一个分布:z1, · · · , zK,满足
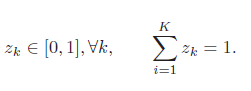
当softmax 函数的输入为K 维向量x 时,
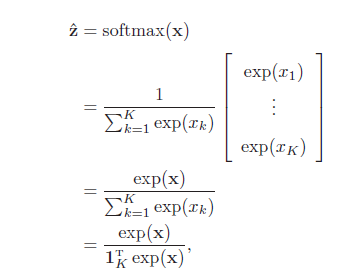
其中,1K = [1, · · · , 1]K×1 是K 维的全1 向量。
其导数为