CodeForces

XOR-pyramid

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

For an array $\mathrm{bb of\; length mm we\; define\; the\; function ff as}$

$\mathrm{f(b)=\{b[1]if m=1f(b[1]\oplus b[2],b[2]\oplus b[3],\dots ,b[m-1]\oplus b[m])otherwise,f(b)=\{b[1]if m=1f(b[1]\oplus b[2],b[2]\oplus b[3],\dots ,b[m-1]\oplus b[m])otherwise,}$

where $\oplus \oplus is bitwise\; exclusive\; OR.$

For example, $\mathrm{f(1,2,4,8)=f(1\oplus 2,2\oplus 4,4\oplus 8)=f(3,6,12)=f(3\oplus 6,6\oplus 12)=f(5,10)=f(5\oplus 10)=f(15)=15f(1,2,4,8)=f(1\oplus 2,2\oplus 4,4\oplus 8)=f(3,6,12)=f(3\oplus 6,6\oplus 12)=f(5,10)=f(5\oplus 10)=f(15)=15}$

You are given an array $\mathrm{aa and\; a\; few\; queries.\; Each\; query\; is\; represented\; as\; two\; integers ll and rr.\; The\; answer\; is\; the\; maximum\; value\; of ff on\; all\; continuous\; subsegments\; of\; the\; array al,al+1,\dots ,aral,al+1,\dots ,ar.}$

Input

The first line contains a single integer $\mathrm{nn (1\le n\le 50001\le n\le 5000) —\; the\; length\; of aa.}$

The second line contains $\mathrm{nn integers a1,a2,\dots ,ana1,a2,\dots ,an (0\le ai\le 230-10\le ai\le 230-1) —\; the\; elements\; of\; the\; array.}$

The third line contains a single integer $\mathrm{qq (1\le q\le 1000001\le q\le 100000) —\; the\; number\; of\; queries.}$

Each of the next $\mathrm{qq lines\; contains\; a\; query\; represented\; as\; two\; integers ll, rr (1\le l\le r\le n1\le l\le r\le n).}$

Output

Print $\mathrm{qq lines —\; the\; answers\; for\; the\; queries.}$

Examples

input

Copy

3
8 4 1
2
2 3
1 2

output

Copy

5
12

input

Copy

6
1 2 4 8 16 32
4
1 6
2 5
3 4
1 2

output

Copy

60
30
12
3

Note

In first sample in both queries the maximum value of the function is reached on the subsegment that is equal to the whole segment.

In second sample, optimal segment for first query are $[3,6][3,6],\; for\; second\; query\; — [2,5][2,5],\; for\; third\; — [3,4][3,4],\; for\; fourth\; — [1,2][1,2].$

$给n个数，询问q次，每次询问给出l,r.\; \; [l,r]区间求异或最大值为多少。一开始没看清是最大值，还以为题目错了。$

$区间【1,6】和区间【2,5】比较一下就知道很多会重复，所以把它们记下来节省时间。$

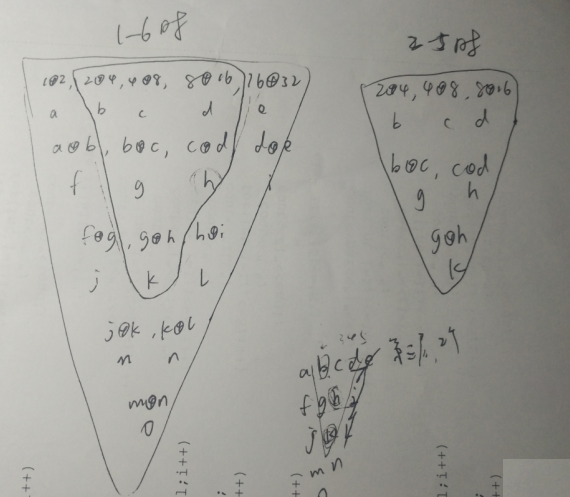
此题需要记忆化两次。区间动态规划。

$我用b数组来存储所以异或的值，dp数来存储最大值。$

$拿第二个样例：$

$b数组这样得来：$

$b[1]这一排还是a数组$

$b[i][j]=b[i-1][j]^b[i-1][j+1];$

$dp数组这样的来：$

$dp[0]这一排还是a数组$

dp[i][j]=max( dp[i-1][j], dp[i-1][j+1]，b[i][j] );

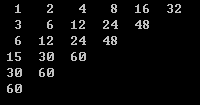$这是dp数组$

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define maxn 110
#define maxm 10010
#define inf 0x3f3f3f
using namespace std;
int b[5005][5005];
int dp[5005][5005];
int a[5005];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        dp[0][i]=a[i];
    }
    for(int i=1;i<=n-1;i++)
    {
        b[1][i]=a[i]^a[i+1];
        dp[1][i]=max(a[i],a[i+1]);//第一排也是要比较得到dp[1][i]，否则第三个样例wa
        dp[1][i]=max(b[1][i],dp[1][i]);
    }
    for(int i=2;i<=n-1;i++)
    {
        for(int j=1;j<=n-i;j++)
        {
            b[i][j]=b[i-1][j]^b[i-1][j+1];
        }
    }
    for(int i=2;i<=n-1;i++)
    {
        for(int j=1;j<=n-i;j++)
        {
            dp[i][j]=max(dp[i-1][j],dp[i-1][j+1]);
            dp[i][j]=max(dp[i][j],b[i][j]);
        }
    }
    for(int i=0;i<=n-1;i++)
    {
        for(int j=1;j<=n-i;j++)
        {
            printf("%4d",dp[i][j]);
        }
        cout<<endl;
    }
    int q;
    scanf("%d",&q);
    while(q--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d
",dp[r-l][l]);
    }
    return 0;
}