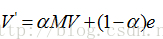一、什么是pagerank
PageRank的Page可是认为是网页,表示网页排名,也可以认为是Larry Page(google 产品经理),因为他是这个算法的发明者之一,还是google CEO(^_^)。PageRank算法计算每一个网页的PageRank值,然后根据这个值的大小对网页的重要性进行排序。它的思想是模拟一个悠闲的上网者,上网者首先随机选择一个网页打开,然后在这个网页上呆了几分钟后,跳转到该网页所指向的链接,这样无所事事、漫无目的地在网页上跳来跳去,PageRank就是估计这个悠闲的上网者分布在各个网页上的概率。
PageRank的核心思想非常简单:
如果一个网页被很多其他网页链接到的话说明这个网页比较重要,也就是PageRank值会相对较高
如果一个PageRank值很高的网页链接到一个其他的网页,那么被链接到的网页的PageRank值会相应地因此而提高
二、最简单pagerank模型
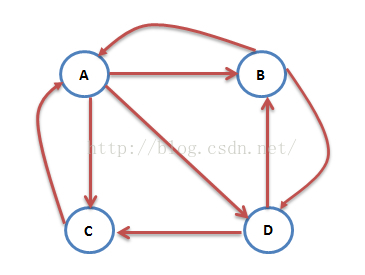
互联网中的网页可以看出是一个有向图,其中网页是结点,如果网页A有链接到网页B,则存在一条有向边A->B,下面是一个简单的示例:
这个例子中只有四个网页,如果当前在A网页,那么悠闲的上网者将会各以1/3的概率跳转到B、C、D,这里的3表示A有3条出链,如果一个网页有k条出链,那么跳转任意一个出链上的概率是1/k,同理D到B、C的概率各为1/2,而B到C的概率为0。一般用转移矩阵表示上网者的跳转概率,如果用n表示网页的数目,则转移矩阵M是一个n*n的方阵;如果网页j有k个出链,那么对每一个出链指向的网页i,有M[i][j]=1/k,而其他网页的M[i][j]=0;上面示例图对应的转移矩阵如下:
初试时,假设上网者在每一个网页的概率都是相等的,即1/n,于是初试的概率分布就是一个所有值都为1/n的n维列向量V0,用V0去右乘转移矩阵M,就得到了第一步之后上网者的概率分布向量MV0,(nXn)*(nX1)依然得到一个nX1的矩阵。下面是V1的计算过程:
注意矩阵M中M[i][j]不为0表示用一个链接从j指向i,M的第一行乘以V0,表示累加所有网页到网页A的概率即得到9/24。得到了V1后,再用V1去右乘M得到V2,一直下去,最终V会收敛,即Vn=MV(n-1),上面的图示例,不断的迭代,最终V=[3/9,2/9,2/9,2/9]‘:
三、终止点问题
上述上网者的行为是一个马尔科夫过程的实例,要满足收敛性,需要具备一个条件:
- 图是强连通的,即从任意网页可以到达其他任意网页:
互联网上的网页不满足强连通的特性,因为有一些网页不指向任何网页,如果按照上面的计算,上网者到达这样的网页后便走投无路、四顾茫然,导致前面累计得到的转移概率被清零,这样下去,最终的得到的概率分布向量所有元素几乎都为0。假设我们把上面图中C到A的链接丢掉,C变成了一个终止点,得到下面这个图:
对应的转移矩阵为:
连续迭代下去,最终所有元素都为0:
四、陷阱问题
另外一个问题就是陷阱问题,即有些网页不存在指向其他网页的链接,但存在指向自己的链接。比如下面这个图:
上网者跑到C网页后,就像跳进了陷阱,陷入了漩涡,再也不能从C中出来,将最终导致概率分布值全部转移到C上来,这使得其他网页的概率分布值为0,从而整个网页排名就失去了意义。如果按照上面图对应的转移矩阵为:
不断的迭代下去,就变成了这样:
五、解决终止点问题和陷阱问题
上面过程,我们忽略了一个问题,那就是上网者是一个悠闲的上网者,而不是一个愚蠢的上网者,我们的上网者是聪明而悠闲,他悠闲,漫无目的,总是随机的选择网页,他聪明,在走到一个终结网页或者一个陷阱网页(比如两个示例中的C),不会傻傻的干着急,他会在浏览器的地址随机输入一个地址,当然这个地址可能又是原来的网页,但这里给了他一个逃离的机会,让他离开这万丈深渊。模拟聪明而又悠闲的上网者,对算法进行改进,每一步,上网者可能都不想看当前网页了,不看当前网页也就不会点击上面的连接,而上悄悄地在地址栏输入另外一个地址,而在地址栏输入而跳转到各个网页的概率是1/n。假设上网者每一步查看当前网页的概率为a,那么他从浏览器地址栏跳转的概率为(1-a),于是原来的迭代公式转化为:
现在我们来计算带陷阱的网页图的概率分布:
重复迭代下去,得到:
六、用Python实现Page Rank算法
Python 实现的PageRank算法,纯粹使用python原生模块,没有使用numpy、scipy。这个程序实现还比较原始,可优化的地方较多。
# -*- coding:utf-8 -*-
import random
N = 4 # 四个网页
d = 0.85 # 阻尼因子为0.85
delt = 0.00001 # 迭代控制变量
# 两个矩阵相乘
def matrix_multi(A, B):
result = [[0] * len(B[0]) for i in range(len(A))]
for i in range(len(A)):
for j in range(len(B[0])):
for k in range(len(B)):
result[i][j] += A[i][k] * B[k][j]
return result
# 矩阵A的每个元素都乘以n
def matrix_multiN(n, A):
result = [[1] * len(A[0]) for i in range(len(A))]
for i in range(len(A)):
for j in range(len(A[0])):
result[i][j] = n * A[i][j]
return result
# 两个矩阵相加
def matrix_add(A, B):
if len(A[0]) != len(B[0]) and len(A) != len(B):
return
result = [[0] * len(A[0]) for i in range(len(A))]
for i in range(len(A)):
for j in range(len(A[0])):
result[i][j] = A[i][j] + B[i][j]
return result
def pageRank(A):
e = []
for i in range(N):
e.append(1)
norm = 100
New_P = []
for i in range(N):
New_P.append([random.random()])
r = [[(1 - d) * i * 1 / N] for i in e]
while norm > delt:
P = New_P
New_P = matrix_add(r, matrix_multiN(d, matrix_multi(A, P))) # P=(1-d)*e/n+d*M'P PageRank算法的核心
norm = 0
# 求解矩阵一阶范数
for i in range(N):
norm += abs(New_P[i][0] - P[i][0])
print New_P
# 根据邻接矩阵求转移概率矩阵并转向
def tran_and_convert(A):
result = [[0] * len(A[0]) for i in range(len(A))]
result_convert = [[0] * len(A[0]) for i in range(len(A))]
for i in range(len(A)):
for j in range(len(A[0])):
result[i][j] = A[i][j] * 1.0 / sum(A[i])
for i in range(len(result)):
for j in range(len(result[0])):
result_convert[i][j] = result[j][i]
return result_convert
def main():
A = [[0, 1, 1, 0],
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 1, 0, 0]]
M = tran_and_convert(A)
pageRank(M)
if __name__ == '__main__':
main()还有另外一个算法是用了numpy数组的
# -*- coding: utf-8 -*-
from numpy import *
a = array([[0, 1, 1, 0],
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 1, 0, 0]], dtype=float) # dtype指定为float
def graphMove(a): # 构造转移矩阵
b = transpose(a) # b为a的转置矩阵
c = zeros((a.shape), dtype=float)
for i in range(a.shape[0]):
for j in range(a.shape[1]):
c[i][j] = a[i][j] / (b[j].sum()) # 完成初始化分配
# print c,"
===================================================="
return c
def firstPr(c): # pr值得初始化
pr = zeros((c.shape[0], 1), dtype=float) # 构造一个存放pr值得矩阵
for i in range(c.shape[0]):
pr[i] = float(1) / c.shape[0]
# print pr,"
==================================================="
return pr
def pageRank(p, m, v): # 计算pageRank值
while ((v == p * dot(m, v) + (
1 - p) * v).all() == False): # 判断pr矩阵是否收敛,(v == p*dot(m,v) + (1-p)*v).all()判断前后的pr矩阵是否相等,若相等则停止循环
# print v
v = p * dot(m, v) + (1 - p) * v
# print (v == p*dot(m,v) + (1-p)*v).all()
return v
if __name__ == "__main__":
M = graphMove(a)
pr = firstPr(M)
p = 0.85 # 引入浏览当前网页的概率为p,假设p=0.8
print pageRank(p, M, pr) # 计算pr值幂迭代法的代码
import numpy as np
class CPageRank(object):
'''实现PageRank Alogrithm
'''
def __init__(self):
self.PR = [] #PageRank值
def GetPR(self, IOS, alpha, max_itrs, min_delta):
'''幂迭代方法求PR值
:param IOS 表示网页出链入链关系的矩阵,是一个左出链矩阵
:param alpha 阻尼系数α,一般alpha取值0.85
:param max_itrs 最大迭代次数
:param min_delta 停止迭代的阈值
'''
#IOS左出链矩阵, a阻尼系数alpha, N网页总数
N = np.shape(IOS)[0]
#所有分量都为1的列向量
e = np.ones(shape=(N, 1))
#计算网页出链个数统计
L = [np.count_nonzero(e) for e in IOS.T]
#计算网页PR贡献矩阵helpS,是一个左贡献矩阵
helps_efunc = lambda ios,l:ios/l
helps_func = np.frompyfunc(helps_efunc, 2, 1)
helpS = helps_func(IOS, L)
#P[n+1] = AP[n]中的矩阵A
A = alpha*helpS + ((1-alpha)/N)*np.dot(e, e.T)
print('左出链矩阵:
', IOS)
print('左PR值贡献概率矩阵:
', helpS)
#幂迭代法求PR值
for i in range(max_itrs):
if 0 == np.shape(self.PR)[0]: #使用1.0/N初始化PR值表
self.PR = np.full(shape=(N,1), fill_value=1.0/N)
print('初始化的PR值表:', self.PR)
#使用PR[n+1] = APR[n]递推公式,求PR[n+1]
old_PR = self.PR
self.PR = np.dot(A, self.PR)
#如果所有网页PR值的前后误差 都小于 自定义的误差阈值,则停止迭代
D = np.array([old-new for old,new in zip(old_PR, self.PR)])
ret = [e < min_delta for e in D]
if ret.count(True) == N:
print('迭代次数:%d, succeed PR:
'%(i+1), self.PR)
break
return self.PR
def CPageRank_manual():
#表示网页之间的出入链的关系矩阵,是一个左关系矩阵,可以理解成右入链矩阵
#IOS[i, j]表示网页j对网页i有出链
IOS = np.array([[0, 0, 0, 0, 1],
[1, 0, 0, 0, 0],
[1, 0, 0, 0, 0],
[1, 1, 0, 0, 0],
[0, 1, 1, 1, 0]], dtype=float)
pg = CPageRank()
ret = pg.GetPR(IOS, alpha=0.85, max_itrs=100, min_delta=0.0001)
print('最终的PR值:
', ret)
if __name__=='__main__':
CPageRank_manual()运行结果
左出链矩阵:
[[ 0. 0. 0. 0. 1.]
[ 1. 0. 0. 0. 0.]
[ 1. 0. 0. 0. 0.]
[ 1. 1. 0. 0. 0.]
[ 0. 1. 1. 1. 0.]]
左PR值贡献概率矩阵:
[[0.0 0.0 0.0 0.0 1.0]
[0.3333333333333333 0.0 0.0 0.0 0.0]
[0.3333333333333333 0.0 0.0 0.0 0.0]
[0.3333333333333333 0.5 0.0 0.0 0.0]
[0.0 0.5 1.0 1.0 0.0]]
初始化的PR值表: [[ 0.2]
[ 0.2]
[ 0.2]
[ 0.2]
[ 0.2]]
迭代次数:29, succeed PR:
[[0.2962595101978549]
[0.11393416086464467]
[0.11393416086464467]
[0.16239748970660772]
[0.31347467836624976]]
最终的PR值:
[[0.2962595101978549]
[0.11393416086464467]
[0.11393416086464467]
[0.16239748970660772]
[0.31347467836624976]]