Tensorflow暑期实践——单变量线性回归

版权说明:浙江财经大学专业实践深度学习tensorflow——齐峰

单变量线性回归

目录

• 1  单变量线性回归
• 2  使用Tensorflow进行算法设计与训练的核心步骤
• 3  有监督机器学习过程示意图
• 4  Tensorflow实现单变量线性回归
  • 4.1  生成数据
    • 4.1.1  Jupyter使用小技巧
  • 4.2  构建模型
  • 4.3  训练模型
  • 4.4  进行预测
• 5  小结

使用Tensorflow进行算法设计与训练的核心步骤

• ** （1）生成数据 **
• ** （2）构建模型 **
• ** （3）训练模型 **
• ** （4）进行预测 **

上述步骤是我们使用Tensorflow进行算法设计与训练的核心步骤，贯穿于后面介绍的具体实战中。
本章用一个简单的例子来讲解这几个步骤。

有监督机器学习过程示意图

Tensorflow实现单变量线性回归

假设我们要学习的函数为线性函数$ y=2x+1 $

生成数据

#在Jupyter中，使用matplotlib显示图像需要设置为 inline 模式，否则不会显示图像
%matplotlib inline

import matplotlib.pyplot as plt # 载入matplotlib
import numpy as np # 载入numpy
import tensorflow as tf # 载入Tensorflow
import os

os.environ['TF_CPP_MIN_LOG_LEVEAL'] = '2'

np.random.seed(5)

** 首先，生成输入数据。 **
我们需要构造满足这个函数的(x)和(y)同时加入一些不满足方程的噪声.

x_data = np.linspace(-1, 1, 100) #直接采用np生成等差数列的方法，生成100个点，每个点的取值在-1~1之间
y_data = 2 * x_data + 1.0 + np.random.randn(*x_data.shape) * 0.4  # y = 2x +1 + 噪声， 其中，噪声的维度与x_data一致

Jupyter使用小技巧

可以使用Tab健进行代码补齐

** 利用matplotlib画图 **

plt.figure() 
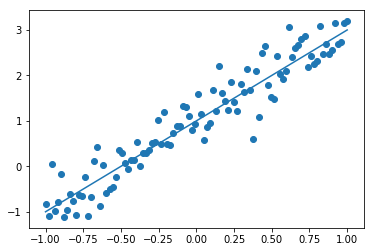
plt.scatter(x_data, y_data) #画出随机生成数据的散点图

plt.scatter(x_data, y_data) 
plt.plot (x_data, 1.0 + 2 * x_data) # 画出我们想要学习到的线性函数 y = 2x +1

构建模型

** 定义(x)和(y)的占位符 **

x = tf.placeholder("float", name = "x") 
y = tf.placeholder("float", name = "y")

** 构建回归模型 **

def model(x, w, b):
    return tf.multiply(x, w) + b 

** 创建变量 **

• Tensorflow变量的声明函数是tf.Variable
• tf.Variable的作用是保存和更新参数
• 变量的初始值可以是随机数、常数，或是通过其他变量的初始值计算得到

w = tf.Variable(-1.0, name="w0") # 构建线性函数的斜率
b = tf.Variable(0.0, name="b0")   # 构建线性函数的截距

pred = model(x, w, b) # pred是预测值

训练模型

** 设置训练参数 **

train_epochs = 30 # 迭代次数
learning_rate = 0.05 #学习率

** 关于学习率（learning_rate）的设置 **

• 学习率的作用：控制参数更新的幅度。
• 如果学习率设置过大，可能导致参数在极值附近来回摇摆，无法保证收敛。
• 如果学习率设置过小，虽然能保证收敛，但优化速度会大大降低，我们需要更多迭代次数才能达到较理想的优化效果。

** 定义损失函数 **

• 损失函数用于描述预测值与真实值之间的误差，从而指导模型收敛方向
• 常见损失函数：均方差（Mean Square Error, MSE）和交叉熵（cross-entropy）

# loss_function = tf.pow(y-pred, 2) # 采用方差作为损失函数

loss_function = tf.reduce_mean(tf.pow((y-pred),2))  # 本例中采用均方差作为损失函数

** 选择优化器 **

optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)# 梯度下降

** 在训练中显示损失值 **

step = 0
loss_list = []
# 显示损失值 loss
# display_step: 控制报告的粒度
# 例如，如果设为2，则将没训练2个样本输出一次损失值
# 与超参数不同，修改display_step不会更改模型所学习的规律
display_step = 10

** 声明会话 **

sess = tf.Session()

** 变量初始化 **

• 在真正执行计算之前，需将所有变量初始化
• 通过** tf.global_variables_initializer **函数可实现对所有变量的初始化

init = tf.global_variables_initializer()

** 执行训练 **

sess.run(init)

for epoch in range(train_epochs):
    for xs,ys in zip(x_data, y_data):
        _, loss=sess.run([optimizer,loss_function], feed_dict={x: xs, y: ys})      
        loss_list.append(loss)
        step=step+1
        if step % display_step == 0:
            print("训练迭代:",'%02d' % (epoch+1),"Step：%03d" % (step),"loss=",
                  "{:.9f}".format(loss))
    b0temp=b.eval(session=sess)
    w0temp=w.eval(session=sess)
    plt.plot (x_data, b0temp + w0temp * x_data )# 画图

训练迭代: 01 Step：040 loss= 0.075409435
训练迭代: 01 Step：050 loss= 0.277659148
训练迭代: 01 Step：060 loss= 0.109922200
训练迭代: 01 Step：070 loss= 1.018932939
训练迭代: 01 Step：080 loss= 0.111073710
训练迭代: 01 Step：090 loss= 0.175155073
训练迭代: 01 Step：100 loss= 0.711191475
训练迭代: 01 Step：110 loss= 0.140157878
训练迭代: 01 Step：120 loss= 0.000191004
训练迭代: 01 Step：130 loss= 0.191256285
训练迭代: 02 Step：140 loss= 0.443984509
训练迭代: 02 Step：150 loss= 0.052047350
训练迭代: 02 Step：160 loss= 0.000134754
训练迭代: 02 Step：170 loss= 0.362875491
训练迭代: 02 Step：180 loss= 0.015833877
训练迭代: 02 Step：190 loss= 0.003371468
训练迭代: 02 Step：200 loss= 0.158117563
训练迭代: 02 Step：210 loss= 0.000004665
训练迭代: 02 Step：220 loss= 0.086956412
训练迭代: 02 Step：230 loss= 0.056739785
训练迭代: 03 Step：240 loss= 0.053117715
训练迭代: 03 Step：250 loss= 0.081143923
训练迭代: 03 Step：260 loss= 0.000436464
训练迭代: 03 Step：270 loss= 0.329459250
训练迭代: 03 Step：280 loss= 0.026408525
训练迭代: 03 Step：290 loss= 0.009510754
训练迭代: 03 Step：300 loss= 0.129814416
训练迭代: 03 Step：310 loss= 0.000850668
训练迭代: 03 Step：320 loss= 0.101492099
训练迭代: 03 Step：330 loss= 0.049019977
训练迭代: 04 Step：340 loss= 0.037520919
训练迭代: 04 Step：350 loss= 0.083892979
训练迭代: 04 Step：360 loss= 0.000469800
训练迭代: 04 Step：370 loss= 0.326714098
训练迭代: 04 Step：380 loss= 0.027423598
训练迭代: 04 Step：390 loss= 0.010171080
训练迭代: 04 Step：400 loss= 0.127554476
训练迭代: 04 Step：410 loss= 0.001011788
训练迭代: 04 Step：420 loss= 0.102769703
训练迭代: 04 Step：430 loss= 0.048394557
训练迭代: 05 Step：440 loss= 0.036328830
训练迭代: 05 Step：450 loss= 0.084126964
训练迭代: 05 Step：460 loss= 0.000472657
训练迭代: 05 Step：470 loss= 0.326483309
训练迭代: 05 Step：480 loss= 0.027510092
训练迭代: 05 Step：490 loss= 0.010227857
训练迭代: 05 Step：500 loss= 0.127364576
训练迭代: 05 Step：510 loss= 0.001026035
训练迭代: 05 Step：520 loss= 0.102877960
训练迭代: 05 Step：530 loss= 0.048342019
训练迭代: 06 Step：540 loss= 0.036229104
训练迭代: 06 Step：550 loss= 0.084146671
训练迭代: 06 Step：560 loss= 0.000472903
训练迭代: 06 Step：570 loss= 0.326463670
训练迭代: 06 Step：580 loss= 0.027517408
训练迭代: 06 Step：590 loss= 0.010232608
训练迭代: 06 Step：600 loss= 0.127348661
训练迭代: 06 Step：610 loss= 0.001027226
训练迭代: 06 Step：620 loss= 0.102886833
训练迭代: 06 Step：630 loss= 0.048337616
训练迭代: 07 Step：640 loss= 0.036220755
训练迭代: 07 Step：650 loss= 0.084148332
训练迭代: 07 Step：660 loss= 0.000472927
训练迭代: 07 Step：670 loss= 0.326462060
训练迭代: 07 Step：680 loss= 0.027518081
训练迭代: 07 Step：690 loss= 0.010233018
训练迭代: 07 Step：700 loss= 0.127347216
训练迭代: 07 Step：710 loss= 0.001027349
训练迭代: 07 Step：720 loss= 0.102887750
训练迭代: 07 Step：730 loss= 0.048337195
训练迭代: 08 Step：740 loss= 0.036220074
训练迭代: 08 Step：750 loss= 0.084148571
训练迭代: 08 Step：760 loss= 0.000472929
训练迭代: 08 Step：770 loss= 0.326461762
训练迭代: 08 Step：780 loss= 0.027518120
训练迭代: 08 Step：790 loss= 0.010233090
训练迭代: 08 Step：800 loss= 0.127347127
训练迭代: 08 Step：810 loss= 0.001027349
训练迭代: 08 Step：820 loss= 0.102888055
训练迭代: 08 Step：830 loss= 0.048337091
训练迭代: 09 Step：840 loss= 0.036219846
训练迭代: 09 Step：850 loss= 0.084148541
训练迭代: 09 Step：860 loss= 0.000472929
训练迭代: 09 Step：870 loss= 0.326461852
训练迭代: 09 Step：880 loss= 0.027518120
训练迭代: 09 Step：890 loss= 0.010233066
训练迭代: 09 Step：900 loss= 0.127347127
训练迭代: 09 Step：910 loss= 0.001027349
训练迭代: 09 Step：920 loss= 0.102888055
训练迭代: 09 Step：930 loss= 0.048337091
训练迭代: 10 Step：940 loss= 0.036219940
训练迭代: 10 Step：950 loss= 0.084148571
训练迭代: 10 Step：960 loss= 0.000472929
训练迭代: 10 Step：970 loss= 0.326461852
训练迭代: 10 Step：980 loss= 0.027518120
训练迭代: 10 Step：990 loss= 0.010233066
训练迭代: 10 Step：1000 loss= 0.127347127
训练迭代: 10 Step：1010 loss= 0.001027349
训练迭代: 10 Step：1020 loss= 0.102888055
训练迭代: 10 Step：1030 loss= 0.048337091
训练迭代: 11 Step：1040 loss= 0.036219940
训练迭代: 11 Step：1050 loss= 0.084148571
训练迭代: 11 Step：1060 loss= 0.000472929
训练迭代: 11 Step：1070 loss= 0.326461852
训练迭代: 11 Step：1080 loss= 0.027518120
训练迭代: 11 Step：1090 loss= 0.010233066
训练迭代: 11 Step：1100 loss= 0.127347127
训练迭代: 11 Step：1110 loss= 0.001027349
训练迭代: 11 Step：1120 loss= 0.102888055
训练迭代: 11 Step：1130 loss= 0.048337091
训练迭代: 12 Step：1140 loss= 0.036219940
训练迭代: 12 Step：1150 loss= 0.084148571
训练迭代: 12 Step：1160 loss= 0.000472929
训练迭代: 12 Step：1170 loss= 0.326461852
训练迭代: 12 Step：1180 loss= 0.027518120
训练迭代: 12 Step：1190 loss= 0.010233066
训练迭代: 12 Step：1200 loss= 0.127347127
训练迭代: 12 Step：1210 loss= 0.001027349
训练迭代: 12 Step：1220 loss= 0.102888055
训练迭代: 12 Step：1230 loss= 0.048337091
训练迭代: 13 Step：1240 loss= 0.036219940
训练迭代: 13 Step：1250 loss= 0.084148571
训练迭代: 13 Step：1260 loss= 0.000472929
训练迭代: 13 Step：1270 loss= 0.326461852
训练迭代: 13 Step：1280 loss= 0.027518120
训练迭代: 13 Step：1290 loss= 0.010233066
训练迭代: 13 Step：1300 loss= 0.127347127
训练迭代: 13 Step：1310 loss= 0.001027349
训练迭代: 13 Step：1320 loss= 0.102888055
训练迭代: 13 Step：1330 loss= 0.048337091
训练迭代: 14 Step：1340 loss= 0.036219940
训练迭代: 14 Step：1350 loss= 0.084148571
训练迭代: 14 Step：1360 loss= 0.000472929
训练迭代: 14 Step：1370 loss= 0.326461852
训练迭代: 14 Step：1380 loss= 0.027518120
训练迭代: 14 Step：1390 loss= 0.010233066
训练迭代: 14 Step：1400 loss= 0.127347127
训练迭代: 14 Step：1410 loss= 0.001027349
训练迭代: 14 Step：1420 loss= 0.102888055
训练迭代: 14 Step：1430 loss= 0.048337091
训练迭代: 15 Step：1440 loss= 0.036219940
训练迭代: 15 Step：1450 loss= 0.084148571
训练迭代: 15 Step：1460 loss= 0.000472929
训练迭代: 15 Step：1470 loss= 0.326461852
训练迭代: 15 Step：1480 loss= 0.027518120
训练迭代: 15 Step：1490 loss= 0.010233066
训练迭代: 15 Step：1500 loss= 0.127347127
训练迭代: 15 Step：1510 loss= 0.001027349
训练迭代: 15 Step：1520 loss= 0.102888055
训练迭代: 15 Step：1530 loss= 0.048337091
训练迭代: 16 Step：1540 loss= 0.036219940
训练迭代: 16 Step：1550 loss= 0.084148571
训练迭代: 16 Step：1560 loss= 0.000472929
训练迭代: 16 Step：1570 loss= 0.326461852
训练迭代: 16 Step：1580 loss= 0.027518120
训练迭代: 16 Step：1590 loss= 0.010233066
训练迭代: 16 Step：1600 loss= 0.127347127
训练迭代: 16 Step：1610 loss= 0.001027349
训练迭代: 16 Step：1620 loss= 0.102888055
训练迭代: 16 Step：1630 loss= 0.048337091
训练迭代: 17 Step：1640 loss= 0.036219940
训练迭代: 17 Step：1650 loss= 0.084148571
训练迭代: 17 Step：1660 loss= 0.000472929
训练迭代: 17 Step：1670 loss= 0.326461852
训练迭代: 17 Step：1680 loss= 0.027518120
训练迭代: 17 Step：1690 loss= 0.010233066
训练迭代: 17 Step：1700 loss= 0.127347127
训练迭代: 17 Step：1710 loss= 0.001027349
训练迭代: 17 Step：1720 loss= 0.102888055
训练迭代: 17 Step：1730 loss= 0.048337091
训练迭代: 18 Step：1740 loss= 0.036219940
训练迭代: 18 Step：1750 loss= 0.084148571
训练迭代: 18 Step：1760 loss= 0.000472929
训练迭代: 18 Step：1770 loss= 0.326461852
训练迭代: 18 Step：1780 loss= 0.027518120
训练迭代: 18 Step：1790 loss= 0.010233066
训练迭代: 18 Step：1800 loss= 0.127347127
训练迭代: 18 Step：1810 loss= 0.001027349
训练迭代: 18 Step：1820 loss= 0.102888055
训练迭代: 18 Step：1830 loss= 0.048337091
训练迭代: 19 Step：1840 loss= 0.036219940
训练迭代: 19 Step：1850 loss= 0.084148571
训练迭代: 19 Step：1860 loss= 0.000472929
训练迭代: 19 Step：1870 loss= 0.326461852
训练迭代: 19 Step：1880 loss= 0.027518120
训练迭代: 19 Step：1890 loss= 0.010233066
训练迭代: 19 Step：1900 loss= 0.127347127
训练迭代: 19 Step：1910 loss= 0.001027349
训练迭代: 19 Step：1920 loss= 0.102888055
训练迭代: 19 Step：1930 loss= 0.048337091
训练迭代: 20 Step：1940 loss= 0.036219940
训练迭代: 20 Step：1950 loss= 0.084148571
训练迭代: 20 Step：1960 loss= 0.000472929
训练迭代: 20 Step：1970 loss= 0.326461852
训练迭代: 20 Step：1980 loss= 0.027518120
训练迭代: 20 Step：1990 loss= 0.010233066
训练迭代: 20 Step：2000 loss= 0.127347127
训练迭代: 20 Step：2010 loss= 0.001027349
训练迭代: 20 Step：2020 loss= 0.102888055
训练迭代: 20 Step：2030 loss= 0.048337091
训练迭代: 21 Step：2040 loss= 0.036219940
训练迭代: 21 Step：2050 loss= 0.084148571
训练迭代: 21 Step：2060 loss= 0.000472929
训练迭代: 21 Step：2070 loss= 0.326461852
训练迭代: 21 Step：2080 loss= 0.027518120
训练迭代: 21 Step：2090 loss= 0.010233066
训练迭代: 21 Step：2100 loss= 0.127347127
训练迭代: 21 Step：2110 loss= 0.001027349
训练迭代: 21 Step：2120 loss= 0.102888055
训练迭代: 21 Step：2130 loss= 0.048337091
训练迭代: 22 Step：2140 loss= 0.036219940
训练迭代: 22 Step：2150 loss= 0.084148571
训练迭代: 22 Step：2160 loss= 0.000472929
训练迭代: 22 Step：2170 loss= 0.326461852
训练迭代: 22 Step：2180 loss= 0.027518120
训练迭代: 22 Step：2190 loss= 0.010233066
训练迭代: 22 Step：2200 loss= 0.127347127
训练迭代: 22 Step：2210 loss= 0.001027349
训练迭代: 22 Step：2220 loss= 0.102888055
训练迭代: 22 Step：2230 loss= 0.048337091
训练迭代: 23 Step：2240 loss= 0.036219940
训练迭代: 23 Step：2250 loss= 0.084148571
训练迭代: 23 Step：2260 loss= 0.000472929
训练迭代: 23 Step：2270 loss= 0.326461852
训练迭代: 23 Step：2280 loss= 0.027518120
训练迭代: 23 Step：2290 loss= 0.010233066
训练迭代: 23 Step：2300 loss= 0.127347127
训练迭代: 23 Step：2310 loss= 0.001027349
训练迭代: 23 Step：2320 loss= 0.102888055
训练迭代: 23 Step：2330 loss= 0.048337091
训练迭代: 24 Step：2340 loss= 0.036219940
训练迭代: 24 Step：2350 loss= 0.084148571
训练迭代: 24 Step：2360 loss= 0.000472929
训练迭代: 24 Step：2370 loss= 0.326461852
训练迭代: 24 Step：2380 loss= 0.027518120
训练迭代: 24 Step：2390 loss= 0.010233066
训练迭代: 24 Step：2400 loss= 0.127347127
训练迭代: 24 Step：2410 loss= 0.001027349
训练迭代: 24 Step：2420 loss= 0.102888055
训练迭代: 24 Step：2430 loss= 0.048337091
训练迭代: 25 Step：2440 loss= 0.036219940
训练迭代: 25 Step：2450 loss= 0.084148571
训练迭代: 25 Step：2460 loss= 0.000472929
训练迭代: 25 Step：2470 loss= 0.326461852
训练迭代: 25 Step：2480 loss= 0.027518120
训练迭代: 25 Step：2490 loss= 0.010233066
训练迭代: 25 Step：2500 loss= 0.127347127
训练迭代: 25 Step：2510 loss= 0.001027349
训练迭代: 25 Step：2520 loss= 0.102888055
训练迭代: 25 Step：2530 loss= 0.048337091
训练迭代: 26 Step：2540 loss= 0.036219940
训练迭代: 26 Step：2550 loss= 0.084148571
训练迭代: 26 Step：2560 loss= 0.000472929
训练迭代: 26 Step：2570 loss= 0.326461852
训练迭代: 26 Step：2580 loss= 0.027518120
训练迭代: 26 Step：2590 loss= 0.010233066
训练迭代: 26 Step：2600 loss= 0.127347127
训练迭代: 26 Step：2610 loss= 0.001027349
训练迭代: 26 Step：2620 loss= 0.102888055
训练迭代: 26 Step：2630 loss= 0.048337091
训练迭代: 27 Step：2640 loss= 0.036219940
训练迭代: 27 Step：2650 loss= 0.084148571
训练迭代: 27 Step：2660 loss= 0.000472929
训练迭代: 27 Step：2670 loss= 0.326461852
训练迭代: 27 Step：2680 loss= 0.027518120
训练迭代: 27 Step：2690 loss= 0.010233066
训练迭代: 27 Step：2700 loss= 0.127347127
训练迭代: 27 Step：2710 loss= 0.001027349
训练迭代: 27 Step：2720 loss= 0.102888055
训练迭代: 27 Step：2730 loss= 0.048337091
训练迭代: 28 Step：2740 loss= 0.036219940
训练迭代: 28 Step：2750 loss= 0.084148571
训练迭代: 28 Step：2760 loss= 0.000472929
训练迭代: 28 Step：2770 loss= 0.326461852
训练迭代: 28 Step：2780 loss= 0.027518120
训练迭代: 28 Step：2790 loss= 0.010233066
训练迭代: 28 Step：2800 loss= 0.127347127
训练迭代: 28 Step：2810 loss= 0.001027349
训练迭代: 28 Step：2820 loss= 0.102888055
训练迭代: 28 Step：2830 loss= 0.048337091
训练迭代: 29 Step：2840 loss= 0.036219940
训练迭代: 29 Step：2850 loss= 0.084148571
训练迭代: 29 Step：2860 loss= 0.000472929
训练迭代: 29 Step：2870 loss= 0.326461852
训练迭代: 29 Step：2880 loss= 0.027518120
训练迭代: 29 Step：2890 loss= 0.010233066
训练迭代: 29 Step：2900 loss= 0.127347127
训练迭代: 29 Step：2910 loss= 0.001027349
训练迭代: 29 Step：2920 loss= 0.102888055
训练迭代: 29 Step：2930 loss= 0.048337091
训练迭代: 30 Step：2940 loss= 0.036219940
训练迭代: 30 Step：2950 loss= 0.084148571
训练迭代: 30 Step：2960 loss= 0.000472929
训练迭代: 30 Step：2970 loss= 0.326461852
训练迭代: 30 Step：2980 loss= 0.027518120
训练迭代: 30 Step：2990 loss= 0.010233066
训练迭代: 30 Step：3000 loss= 0.127347127
训练迭代: 30 Step：3010 loss= 0.001027349
训练迭代: 30 Step：3020 loss= 0.102888055
训练迭代: 30 Step：3030 loss= 0.048337091

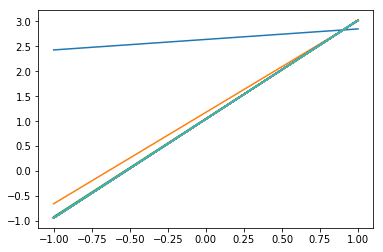
从上图可以看出，由于本案例所拟合的模型较简单，训练3次之后已经接近收敛。
对于复杂模型，需要更多次训练才能收敛。

** 打印结果 **

print  ("w：", sess.run(w)) # w的值应该在2附近 
print ("b：", sess.run(b)) # b的值应该在1附近 

w： 1.9822965
b： 1.0420127

** 可视化 **

plt.scatter(x_data,y_data,label='Original data')
plt.plot (x_data, x_data * sess.run(w) + sess.run(b),label='Fitted line',color='r',linewidth=3)
plt.legend(loc=2)# 通过参数loc指定图例位置

图形化显示损失值

plt.plot(loss_list)

plt.plot(loss_list,'r+')

进行预测

x_test = 12.0
output = sess.run(w)  * x_test + sess.run(b)
print("预测值：%f" % output)
target = 2 * x_test + 1.0
print("目标值：%f" % target)

预测值：24.829570
目标值：25.000000

** 以上是利用Tensorflow训练一个线性模型并进行预测的完整过程。
通过逐渐降低损失值loss来训练参数(w)和(b)拟合 (y = 2x + 1)中的系数2和1。 **

小结

** 通过一个简单的例子介绍了利用Tensorflow实现机器学习的思路，重点讲解了下述步骤： **

** - （1）生成人工数据集及其可视化 **

** - （2）构建线性模型 **

** - （3）定义损失函数 **

** - （4）最小化损失函数 **

** - （5）训练结果的可视化 **

** - （6）利用学习到的模型进行预测 **