PAT 甲级 1146 Topological Order (25 分)(拓扑较简单，保存入度数和出度的节点即可)

1146 Topological Order (25 分)

 

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

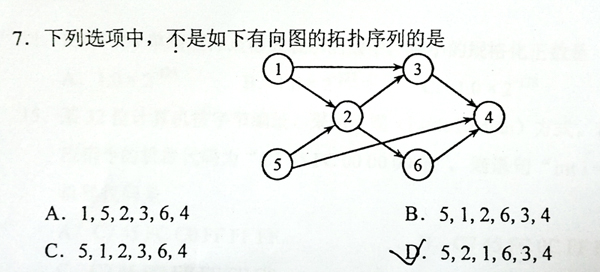
Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

3 4

题意：

做这题之前首先要先去了解什么是拓扑排序，可以参考https://blog.csdn.net/qq_35644234/article/details/60578189

给出一个图，再给几组数据，让你判断这几组数据是否符合拓扑排序 

题解：

保存入度数和出度的节点。用一个数组来统计每个点的入度，vector保存出度的节点，然后就可以开始判断。在判断的时候，将与这个点去掉，就是指这个点连接的所有点的入度都减了1。

AC代码：

#include<bits/stdc++.h> 
using namespace std;
int n,m,u,v;
int in[1005],inx[1005];
vector<int>out[1005];
int main(){
    cin>>n>>m;
    memset(in,0,sizeof(in));
    for(int i=1;i<=m;i++){
        cin>>u>>v;
        out[u].push_back(v);//保存出去的节点 
        in[v]++; //计算入度        
    }
    int k;
    cin>>k;
    int a[105];
    int num=0;
    for(int i=0;i<k;i++){
        int f=1;
        memcpy(inx, in, sizeof(in));//将in拷贝给inx 
        for(int j=1;j<=n;j++){
            cin>>u;
            if(inx[u]!=0||f==0){
                f=0;
                continue;
            }
            for(int p=0;p<out[u].size();p++){//对受影响的节点的入度-- 
                inx[out[u].at(p)]--;
            }
        }
        if(!f){
            a[++num]=i;
        }
    }
    for(int i=1;i<=num;i++){
        cout<<a[i];
        if(i!=num) cout<<" ";
    }
    return 0;
}