Python SciPy库——插值与拟合

插值与拟合

原文链接：https://zhuanlan.zhihu.com/p/28149195

1.最小二乘拟合

实例1

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
## 设置字符集，防止中文乱码
import matplotlib
matplotlib.rcParams['font.sans-serif']=[u'simHei']
matplotlib.rcParams['axes.unicode_minus']=False

plt.figure(figsize=(9,9))
x=np.linspace(0,10,1000)
X = np.array([8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78])
Y = np.array([7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05])
#计算以p为参数的直线和原始数据之间的误差
def f(p):
    k, b = p
    return(Y-(k*X+b))
#leastsq使得f的输出数组的平方和最小，参数初始值为[1,0]
r = leastsq(f, [1,0])
k, b = r[0]
print("k=",k,"b=",b)

plt.scatter(X,Y, s=100, alpha=1.0, marker='o',label=u'数据点')

y=k*x+b

ax = plt.gca()

ax.set_xlabel(..., fontsize=20)
ax.set_ylabel(..., fontsize=20)
#设置坐标轴标签字体大小

plt.plot(x, y, color='r',linewidth=5, linestyle=":",markersize=20, label=u'拟合曲线')

plt.legend(loc=0, numpoints=1)
leg = plt.gca().get_legend()
ltext  = leg.get_texts()
plt.setp(ltext, fontsize='xx-large')

plt.xlabel(u'安培/A')
plt.ylabel(u'伏特/V')

plt.xlim(0, x.max() * 1.1)
plt.ylim(0, y.max() * 1.1)

plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
#刻度字体大小


plt.legend(loc='upper left')

plt.show()

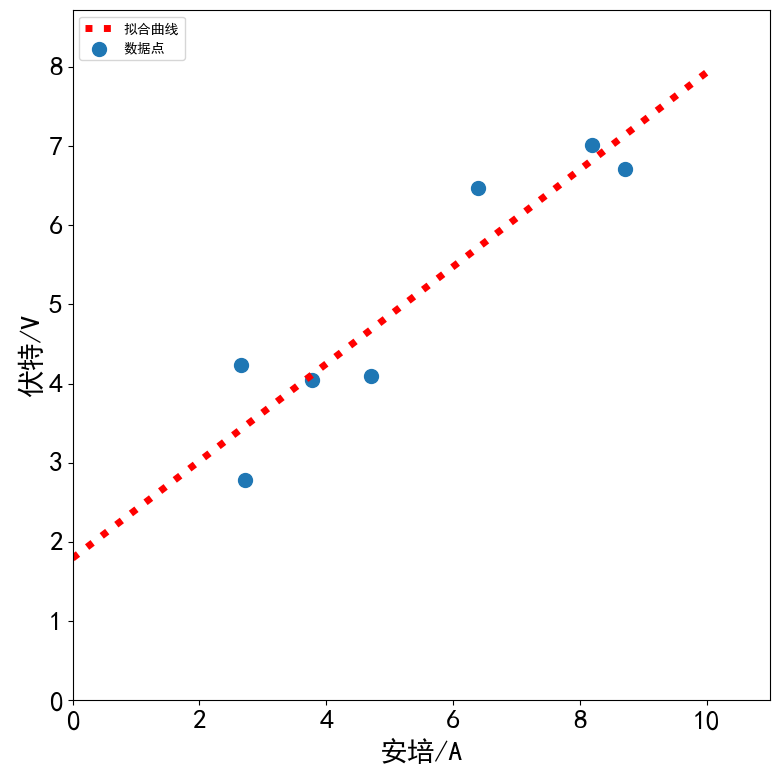
k= 0.6134953491930442 b= 1.794092543259387

实例2

# -*- coding: utf-8 -*-

#最小二乘拟合实例
import numpy as np
from scipy.optimize import leastsq
import pylab as pl
## 设置字符集，防止中文乱码
import matplotlib
matplotlib.rcParams['font.sans-serif']=[u'simHei']
matplotlib.rcParams['axes.unicode_minus']=False

def func(x, p):
    """
    数据拟合所用的函数: A*cos(2*pi*k*x + theta)
    """
    A, k, theta = p
    return A*np.sin(k*x+theta)   

def residuals(p, y, x):
    """
    实验数据x, y和拟合函数之间的差，p为拟合需要找到的系数
    """
    return y - func(x, p)

x = np.linspace(0, 20, 100)
A, k, theta = 10, 3, 6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据    

p0 = [10, 0.2, 0] # 第一次猜测的函数拟合参数

# 调用leastsq进行数据拟合
# residuals为计算误差的函数
# p0为拟合参数的初始值
# args为需要拟合的实验数据
plsq = leastsq(residuals, p0, args=(y1, x))

print (u"真实参数:", [A, k, theta] )
print (u"拟合参数", plsq[0]) # 实验数据拟合后的参数

pl.plot(x, y0, color='r',label=u"真实数据")
pl.plot(x, y1, color='b',label=u"带噪声的实验数据")
pl.plot(x, func(x, plsq[0]), color='g', label=u"拟合数据")
pl.legend()
pl.show()

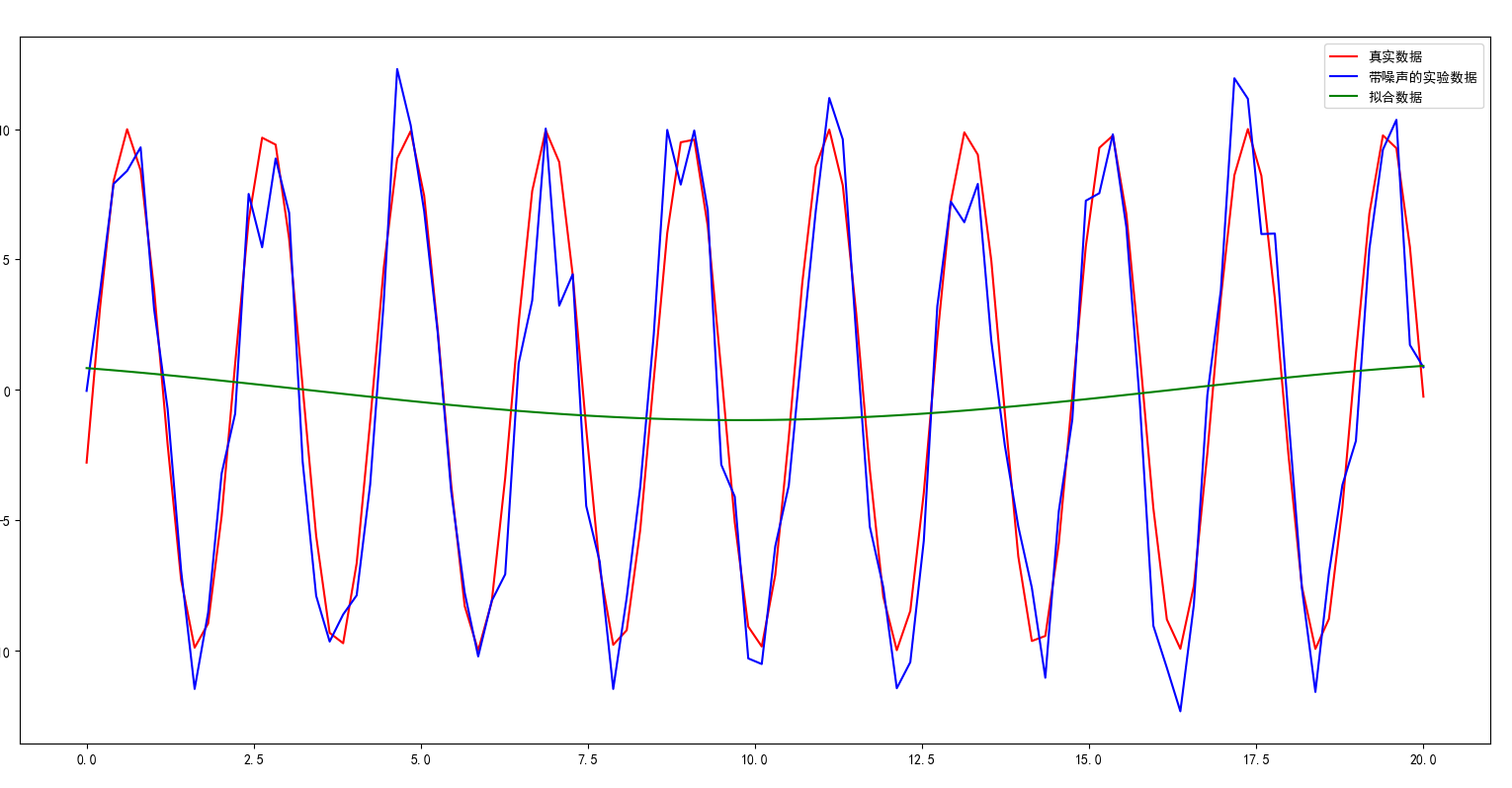
真实参数: [10, 3, 6]
拟合参数 [-1.16428658  0.24215786 -0.794681  ]

2.插值

实例1

# -*- coding: utf-8 -*-

# -*- coding: utf-8 -*-

import numpy as np
import pylab as pl
from scipy import interpolate 
import matplotlib.pyplot as plt
## 设置字符集，防止中文乱码
import matplotlib
matplotlib.rcParams['font.sans-serif']=[u'simHei']
matplotlib.rcParams['axes.unicode_minus']=False

x = np.linspace(0, 2*np.pi+np.pi/4, 10)
y = np.sin(x)

x_new = np.linspace(0, 2*np.pi+np.pi/4, 100)
f_linear = interpolate.interp1d(x, y)
tck = interpolate.splrep(x, y)
y_bspline = interpolate.splev(x_new, tck)

plt.xlabel(u'安培/A')
plt.ylabel(u'伏特/V')

plt.plot(x, y, "o",  label=u"原始数据")
plt.plot(x_new, f_linear(x_new), label=u"线性插值")
plt.plot(x_new, y_bspline, label=u"B-spline插值")

pl.legend()
pl.show()

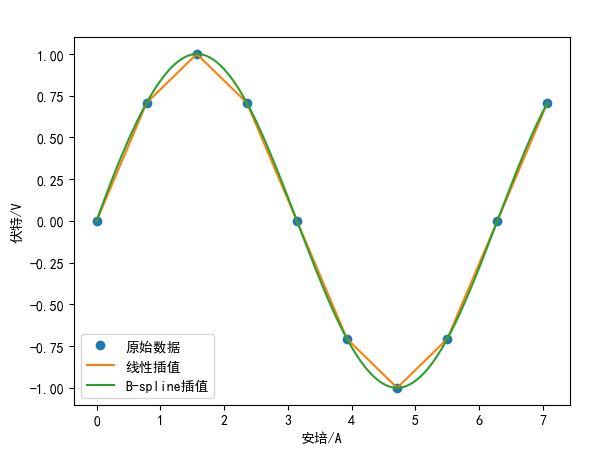
实例2

# -*- coding: utf-8 -*-

import numpy as np
from scipy import interpolate
import pylab as pl
## 设置字符集，防止中文乱码
import matplotlib
matplotlib.rcParams['font.sans-serif']=[u'simHei']
matplotlib.rcParams['axes.unicode_minus']=False

#创建数据点集并绘制
pl.figure(figsize=(12,9))
x = np.linspace(0, 10, 11)
y = np.sin(x)
ax=pl.plot()

pl.plot(x,y,'ro')
#建立插值数据点
xnew = np.linspace(0, 10, 101)
for kind in ['nearest', 'zero','linear','quadratic']:
    #根据kind创建插值对象interp1d
    f = interpolate.interp1d(x, y, kind = kind)
    ynew = f(xnew)#计算插值结果
    pl.plot(xnew, ynew, label = str(kind))

pl.xticks(fontsize=20)
pl.yticks(fontsize=20)

pl.legend(loc = 'lower right')
pl.show()

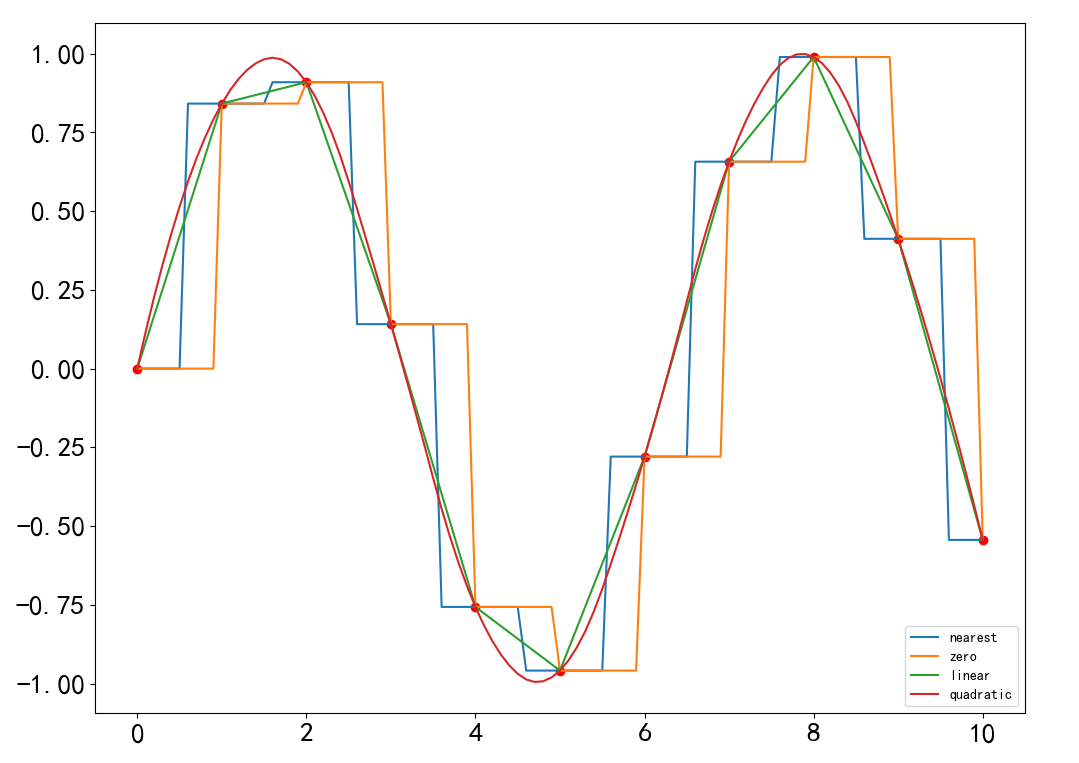
B样条曲线插值
一维数据的插值运算可以通过 interp1d()实现。
其调用形式为：
Interp1d可以计算x的取值范围之内任意点的函数值，并返回新的数组。
interp1d(x, y, kind=‘linear’, …)
参数 x和y是一系列已知的数据点
参数kind是插值类型，可以是字符串或整数

B样条曲线插值
Kind给出了B样条曲线的阶数：
 ‘
zero‘ ‘nearest’ :0阶梯插值，相当于0阶B样条曲线
 ‘slinear’‘linear’ :线性插值，相当于1阶B样条曲线
 ‘quadratic’‘cubic’:2阶和3阶B样条曲线，更高阶的曲线可以直接使用整数值来指定

（1）#创建数据点集：

import numpy as np

x = np.linspace(0, 10, 11)

y = np.sin(x)

 

（2）#绘制数据点集：

import pylab as pl

pl.plot(x,y,'ro')

 

 

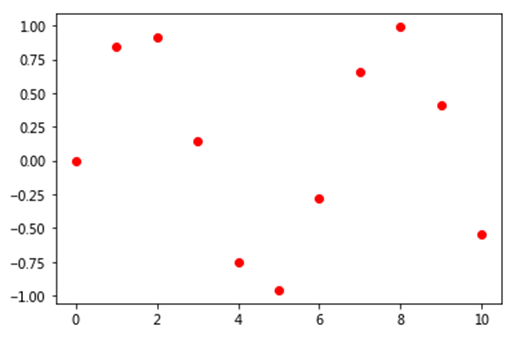
创建interp1d对象f、计算插值结果：
xnew = np.linspace(0, 10, 11)
from scipy import interpolate
f = interpolate.interp1d(x, y, kind = kind)
ynew = f(xnew)

根据kind类型创建interp1d对象f、计算并绘制插值结果：
xnew = np.linspace(0, 10, 11)
for kind in ['nearest', 'zero','linear','quadratic']:
#根据kind创建插值对象interp1d
f = interpolate.interp1d(x, y, kind = kind)
ynew = f(xnew)#计算插值结果
pl.plot(xnew, ynew, label = str(kind))#绘制插值结果

如果我们将代码稍作修改增加一个5阶插值

import numpy as np
from scipy import interpolate
import pylab as pl
#创建数据点集并绘制
pl.figure(figsize=(12,9))
x = np.linspace(0, 10, 11)
y = np.sin(x)
ax=pl.plot()

pl.plot(x,y,'ro')
#建立插值数据点
xnew = np.linspace(0, 10, 101)
for kind in ['nearest', 'zero','linear','quadratic',5]:
    #根据kind创建插值对象interp1d
    f = interpolate.interp1d(x, y, kind = kind)
    ynew = f(xnew)#计算插值结果
    pl.plot(xnew, ynew, label = str(kind))

pl.xticks(fontsize=20)
pl.yticks(fontsize=20)

pl.legend(loc = 'lower right')
pl.show()
运行得到
 

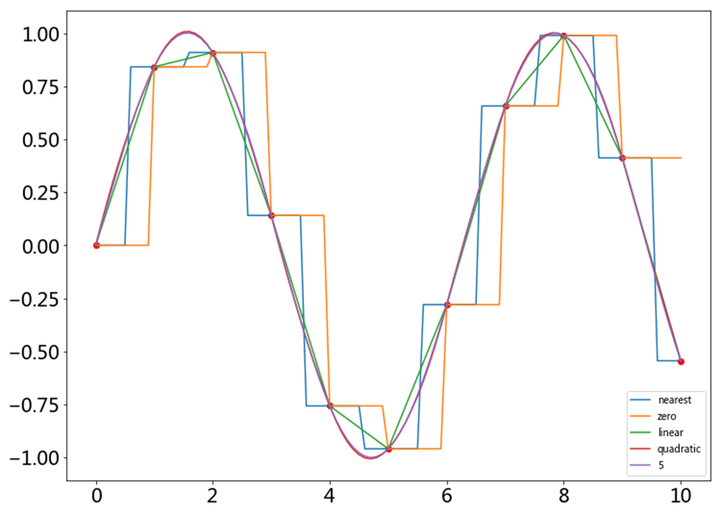
发现5阶已经很接近正弦曲线，但是如果x值选取范围较大，则会出现跳跃。

关于拟合与插值的数学基础可参见霍开拓：拟合与插值的区别？

左边插值，右边拟合