括号序列——我那令人智熄的操作

括号序列

题目描述:

输入格式：

输出格式：

样例输入：

6
0
0
1
1
0
1

样例输出:

3

提示:

解释：

时间限制：1000ms

空间限制:128MByte

这题。。。以前做过题面很想的题目很多，但是这个题意不是很一样。以前做的题面都是问前后括号数量是否匹配，这一个题目则是弄了一个特殊的计算方式来求由括号组成的字符串的值。于是，看到这个题目的一瞬间，模拟！

#include<bits/stdc++.h>
using namespace std;
int a[100000]={0},n,x,num=0,sum=0,ma=0,s=0,re=0,m=-1;
int main(){
	cin>>n;
	for (int i=1; i<=n; i++){
		cin>>x;
		sum%=12345678910;
		if (a[1]==0) {
			s+=re+sum;
			re=0;
			s%=12345678910;
			sum=0;
		}
		if (x==0){
			if (m!=-1 && a[1]!=0) m++;
			re+=sum;
			sum=0;
			ma=0;
			num++;
			a[num]=1;
		}
		else if (x==1){
			if (ma==0 && a[num]==1){
				if (m==-1) m=0;
				if (m!=-1 && m!=0) m--;
				sum+=1;
				a[num]=0;
				num--;
				ma=1;
			}
			else if (ma==1 && a[num]==1){
				if (m!=0){
				sum*=2;
				a[num]=0;
				num--;
				m--;
				}
				else {
					re+=sum;
					re*=2;
					sum=0;
					a[num]=0;
					num--;
				}
			}
		}
	}
	sum%=12345678910;
	s+=sum+re;
	s%=12345678910;
	cout<<s;
	return 0;
}

这个还是我改了很久的代码。到了后来还是只有三十分，剩下的点都WA掉了。然后到了最后还是这个分数。非常的无奈。

后来还是参考了一下大佬的程序，但是有点难理解，后来弄了一下子，最终还是搞懂了。总而言之，还是先贴一下大佬的程序把。

#include<bits/stdc++.h>
using namespace std;
const long long mod=12345678910;
int n,x,cur,pre,cnt;
long long s[100010],sum;
int main(){
	cin>>n;
	for(int i=0;i<n;i++){
		scanf("%d",&x);
		if(x==0) cur++; 
		if(x==1){
		cur--;
		if(pre==0) s[cur]=(s[cur]+1)%mod;
		}
		pre=x;
		cnt=max(cnt,cur);
	}
	for(int i=cnt;i>=0;i--) s[i]=(s[i]+s[i+1]*2)%mod;
	cout<<s[0];return 0;
}

然后用我神乎其技的画技来展示一下大佬的程序，以及解释一下样例吧。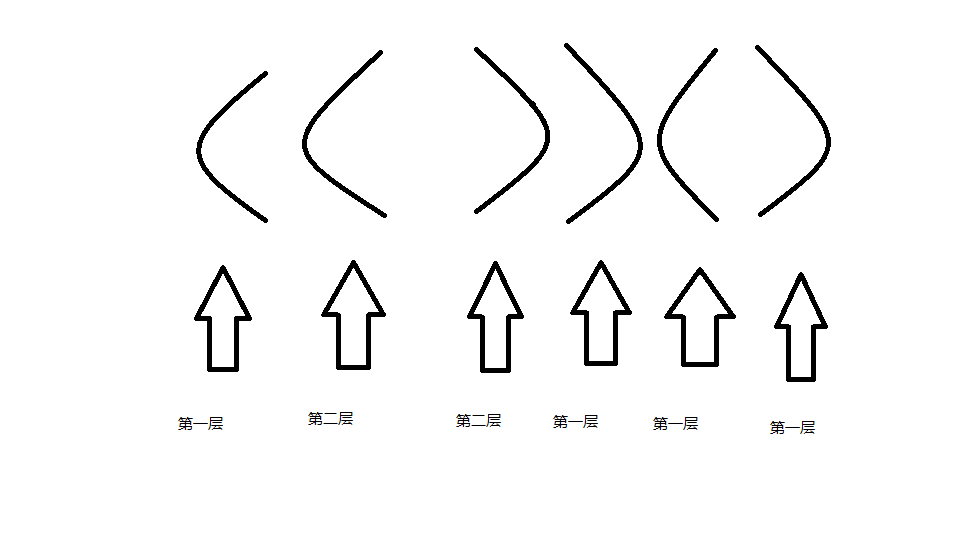

我们将样例中的图画出来就是这个样子的，虽然很丑，但是还是能够勉强看一下的。前面贴出的代码中最迷的就是这个s数组，s数组的下标代表的是括号的层数，如图所示，然后，s[i]就代表在第i层时的分数。我们可以得出一个类似于动态规划的状态转移方程的东西那就是s[i]=(s[i]+s[i-1]*2)%mod;其中要注意的一点就是s[1]代表的是第二层，而不是第一层，s[0]代表的才是第一层。然后接下来要解决的就是如何给每一个括号分层。这里面我们完全不需要考虑运算中的乘的运算，因为我们可以放到外面去算，所以只需要考虑加的运算。

我们用cur这个变量来代表当前所能够到达的层数，然后每次遇到左括号的时候就将cur++，来表示当前层数+1，然后遇到右括号时，需要考虑两种情况，我们用pre这个变量来表示这个右括号之前的符号：1.如果这个右括号之前是左括号，那就不要说什么了cur--，然后将s[cur]++，表示在第cur层的时候分数+1。2.如果这个右括号之前还是右括号，这就表明与这个括号配对的另一个左括号并不是连续的，所以并不是使当前层数总值+1而是*2，就不能将s[cur]++了。然后在代码中的cnt就是用来记录一下最大值来减少在for中循环的次数。

最后我们用一个for循环来执行s[i]=(s[i]+s[i+1]*2)%mod这条语句，最后s[0]就是我们所要求的值了。

呵呵呵，模拟什么的还是去屎把！！！这都是什么操作！感觉自己就是来搞笑的，模拟都模拟不好，后面的点WA了这么多，模拟的太失败了。根本就是吔屎。仰天长啸一句mmp！诶，令人智熄的操作*2.

made by cain-