D

题目链接：http://codeforces.com/problemset/problem/1323/D

Catherine received an array of integers as a gift for March 8. Eventually she grew bored with it, and she started calculated various useless characteristics for it. She succeeded to do it for each one she came up with. But when she came up with another one — xor of all pairwise sums of elements in the array, she realized that she couldn't compute it for a very large array, thus she asked for your help. Can you do it? Formally, you need to compute

(a1+a2)⊕(a1+a3)⊕…⊕(a1+an)⊕(a2+a3)⊕…⊕(a2+an)…⊕(an−1+an)(a1+a2)⊕(a1+a3)⊕…⊕(a1+an)⊕(a2+a3)⊕…⊕(a2+an)…⊕(an−1+an)

Here x⊕yx⊕y is a bitwise XOR operation (i.e. xx ^ yy in many modern programming languages). You can read about it in Wikipedia: https://en.wikipedia.org/wiki/Exclusive_or#Bitwise_operation.

Input

The first line contains a single integer nn (2≤n≤4000002≤n≤400000) — the number of integers in the array.

The second line contains integers a1,a2,…,ana1,a2,…,an (1≤ai≤1071≤ai≤107).

Output

Print a single integer — xor of all pairwise sums of integers in the given array.

Examples

Input

2
1 2

Output

3

Input

3
1 2 3

Output

2

Note

In the first sample case there is only one sum 1+2=31+2=3.

In the second sample case there are three sums: 1+2=31+2=3, 1+3=41+3=4, 2+3=52+3=5. In binary they are represented as 0112⊕1002⊕1012=01020112⊕1002⊕1012=0102, thus the answer is 2.

⊕⊕ is the bitwise xor operation. To define x⊕yx⊕y, consider binary representations of integers xx and yy. We put the ii-th bit of the result to be 1 when exactly one of the ii-th bits of xx and yy is 1. Otherwise, the ii-th bit of the result is put to be 0. For example, 01012⊕00112=0110201012⊕00112=01102.

题意：给出数组a，求出下列式子的值

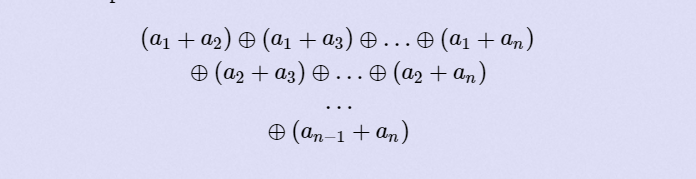
思路：代码中，很详细

看代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<stack>
#include<map>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<stack>
#include<map>
#include<queue>
#include<cmath>
using namespace std;
typedef long long LL;
typedef unsigned long long ull;
#define sc1(a) scanf("%lld",&a)
#define pf1(a) printf("%lld
",a)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
const LL INF=1e18;
const ull base=2333;
const int maxn=4e5+55;
const int maxm=1e4+50;
const int maxv=1e6+5;
const int maxk=1e8+5;
const int mod=1e9+7;
/**
异或的每一位具有独立性，也就是只与该位有关，由于这一特性，我们可以把每一位单独考虑
数据范围是1e7 我们枚举26位就足够了
现在对这26位进行计算，判断每一位为1还是0
现在的问题转变成了怎么计算每一位是1还是0
假设当前枚举到第k位，要判断第k位为1还是0，我们要进行如下操作
首先可以知道k+1...k+n位对第k位是没有影响的，因为是两个数相加，进位也不会影响第k位
所以可以去除掉这些位，得到一个范围在0-(2<<k+1)-1范围内的数组
因为结果是两数相加，所以这个结果的范围也就是[0,(2<<k+2)-2],但是我们要第k位为1
所以取值范围变成[2<<k,(2<<k+1)-1] 和 [(2<<k+1)+(2<<k),(2<<k+2)-2]
此时我们枚举每一个a[i]，知道a[i]了，a[j]的取值范围就是结果的取值范围减去[i]的值
也就是[2<<k-a[i],(2<<k+1)-1-a[i]] 和 [(2<<k+1)+(2<<k)-a[i],(2<<k+2)-2-a[i]]
现在我们就是要得到在这个范围内的数的个数了，这些数都是能和a[i]相加得到第k位为1的
求这个范围内的数，可以通过二分查找即可
*/
LL a[maxn],b[maxn];
int main()
{
    LL N;sc1(N);
    for(LL i=1;i<=N;i++) sc1(a[i]);
    LL ans=0;
    for(LL i=0;i<=26;i++)//枚举每一位
    {
        for(LL j=1;j<=N;j++)
        {
            b[j]=a[j]&((1<<(i+1))-1);
        }
        sort(b+1,b+1+N);
        LL num=0;
        for(LL j=1;j<N;j++)
        {
            num+=upper_bound(b+j+1,b+1+N,((1<<(i+1))-1-b[j]))-lower_bound(b+j+1,b+1+N,(1<<i)-b[j]);
            num+=upper_bound(b+j+1,b+1+N,((1<<(i+2))-2-b[j]))-lower_bound(b+j+1,b+1+N,((1<<(i+1))+(1<<i)-b[j]));
        }
        if(num&1) ans^=(1<<i);
    }
    pf1(ans);
    return 0;
}
/**

*/