题目链接:https://www.luogu.org/problem/P1337
题目描述
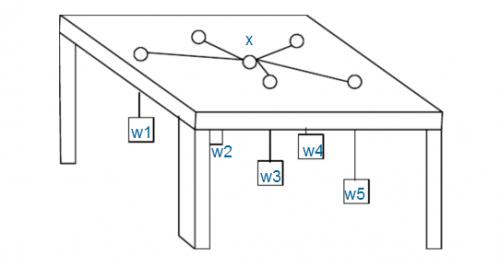
如图:有n个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。
问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
输入格式
文件的第一行为一个正整数n(1≤n≤1000),表示重物和洞的数目。接下来的n行,每行是3个整数:Xi.Yi.Wi,分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )
输出格式
你的程序必须输出两个浮点数(保留小数点后三位),分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。
输入输出样例
输入 #1
3 0 0 1 0 2 1 1 1 1
输出 #1
0.577 1.000
说明/提示
[JSOI]
思路:每个重物对绳结的影响值是该重物的质量*到绳结的距离,我们把这个影响投影到x坐标和y坐标 ,所有点重物的影响叠加起来
分别贪心x坐标和y坐标,就可以得出答案了
看代码:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #include<vector> #include<map> #include<cstdlib> using namespace std; typedef long long LL; const LL mod=1e9+7; const LL INF=1e9+7; const int maxn=1e3+50; const double StartT=50000;//初始温度 1000也可以过这道题 const double rate=0.99;//退火系数 一般0.97-0.99 const double eps=1e-6;//精度 可以在题目要求的小数点后面位数多加3左右 const double FINF=1e18; /** 没有算退火的复杂度 rate=0.98 T=1000 1026次 T=20000 1175次 T=50000 1220次 rate=0.99 T=50000 2452 **/ int N; double px,py;//假设向右和上为正 double ansx,ansy,ans=INF; double prex,prey; struct Node { double x,y,w; Node(){} Node(double x1,double y1,double w1) { x=x1;y=y1;w=w1; } }a[maxn]; void dist(Node n1,Node n2)//n2是当前选中的位置 { double x1=n1.x,y1=n1.y; double x2=n2.x,y2=n2.y; double w=n1.w; //判断n1在n2的第几象限 double dx,dy; double wx,wy; if(x1<x2&&y1<y2)//在第三象限 { dx=x2-x1;dy=y2-y1; wx=w*dx/(sqrt(dy*dy+dx*dx)); wy=w*dy/(sqrt(dy*dy+dx*dx)); px-=wx; py-=wy; } else if(x1>x2&&y1<y2)//第四象限 { dx=x1-x2;dy=y2-y1; wx=w*dx/(sqrt(dy*dy+dx*dx)); wy=w*dy/(sqrt(dy*dy+dx*dx)); px+=wx; py-=wy; } else if(x1>x2&&y1>y2)//第一象限 { dx=x1-x2;dy=y1-y2; wx=w*dx/(sqrt(dy*dy+dx*dx)); wy=w*dy/(sqrt(dy*dy+dx*dx)); px+=wx; py+=wy; } else if(x1<x2&&y1>y2)//第二象限 { dx=x2-x1;dy=y1-y2; wx=w*dx/(sqrt(dy*dy+dx*dx)); wy=w*dy/(sqrt(dy*dy+dx*dx)); px-=wx; py+=wy; } else if(y1==y2)//在同一行 { if(x1<=x2) { wx=w*(x2-x1); px-=wx; } else { wx=w*(x1-x2); px+=wx; } } else if(x1==x2)//在同一列 { if(y1<=y2) { wy=w*(y2-y1); py-=wy; } else { wy=w*(y1-y2); py+=wy; } } return ; } void solve() { double ans=FINF; prex=FINF;prey=FINF; double T=StartT; Node now=Node(0,0,0);//随机选取一个点 while(T>eps) { px=0,py=0; for(int i=1;i<=N;i++)//算出现在的误差 { dist(a[i],now); } //此时两边的误差为px py ///注意这里要分开来贪心 不能直接判断x*x+y*y的大小和之前的比较 ///就是这里卡了一下 不过还是想出来了 if(fabs(prey)>fabs(py))//贪y { prey=py; ansy=now.y; } if(fabs(prex)>fabs(px))//贪x { prex=px; ansx=now.x; } now.x=(now.x+(px)*(T/StartT)); now.y=(now.y+(py)*(T/StartT)); T=T*rate; } // cout<<"sum:"<<sum<<endl; printf("%.3lf %.3lf ",ansx,ansy); } int main() { scanf("%d",&N); for(int i=1;i<=N;i++) { scanf("%lf%lf%lf",&a[i].x,&a[i].y,&a[i].w); } solve(); return 0; }