后缀数组个人感觉的确有点复杂,看了挺久的,听说后缀数组是一种神仙操作,忘记在哪听到这个就学了一下
学习博客:https://www.cnblogs.com/victorique/p/8480093.html
什么是后缀数组
我们先看几条定义:
子串
在字符串s中,取任意i<=j,那么在s中截取从i到j的这一段就叫做s的一个子串
后缀
后缀就是从字符串的某个位置i到字符串末尾的子串,我们定义以s的第i个字符为第一个元素的后缀为suff(i)
后缀数组
把s的每个后缀按照字典序排序,
后缀数组sa[i]就表示排名为i的后缀的起始位置的下标
而它的映射数组rk[i]就表示起始位置的下标为i的后缀的排名
简单来说,sa表示排名为i的是啥,rk表示第i个的排名是啥
一定要记牢这些数组的意思,后面看代码的时候如果记不牢的话就绝对看不懂
后缀数组的思想
先说最暴力的情况,快排(n log n)每个后缀,但是这是字符串,所以比较任意两个后缀的复杂度其实是O(n),这样一来就是接近O(n^2 log n)的复杂度,数据大了肯定是不行的,所以我们这里有两个优化。
ps:本文中的^表示平方而不是异或
倍增
首先读入字符串之后我们现根据单个字符排序,当然也可以理解为先按照每个后缀的第一个字符排序。对于每个字符,我们按照字典序给一个排名(当然可以并列),这里称作关键字。
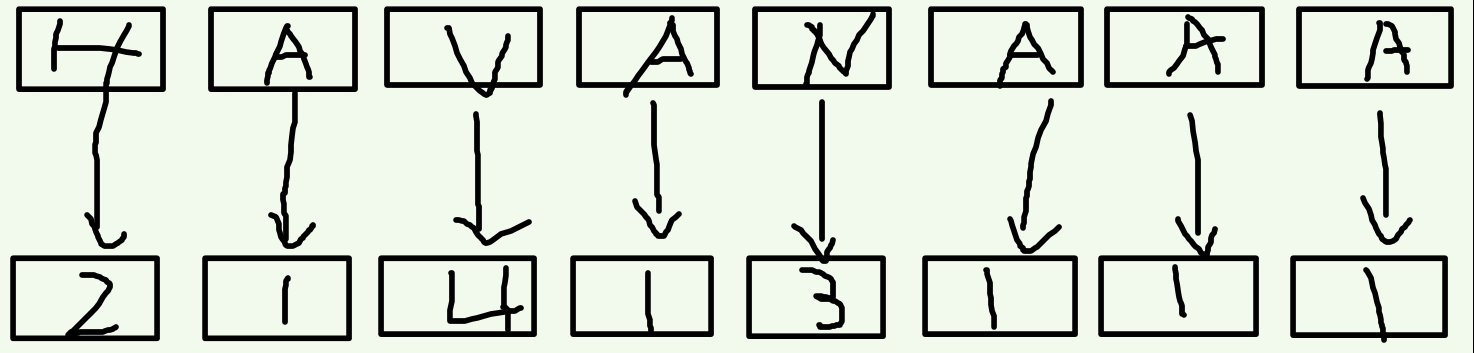
接下来我们再把相邻的两个关键字合并到一起,就相当于根据每一个后缀的前两个字符进行排序。想想看,这样就是以第一个字符(也就是自己本身)的排名为第一关键字,以第二个字符的排名为第二关键字,把组成的新数排完序之后再次标号。没有第二关键字的补零。
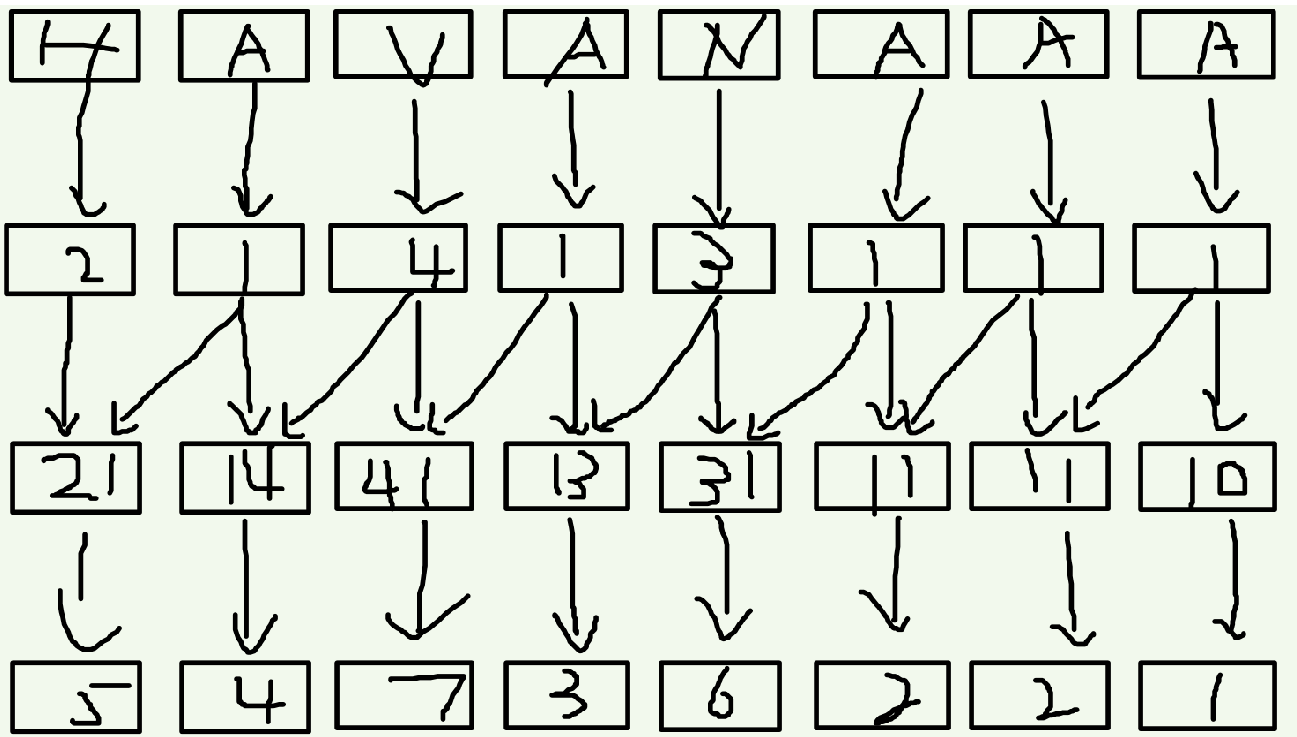
既然是倍增,就要有点倍增的样子。接下来我们对于一个在第i位上的关键字,它的第二关键字就是第(i+2)位置上的,联想一下,因为现在第i位上的关键字是suff(i)的前两个字符的排名,第i+2位置上的关键字是suff(i+2)的前两个字符的排名,这两个一合并,不就是suff(i)的前四个字符的排名吗?方法同上,排序之后重新标号,没有第二关键字的补零。同理我们可以证明,下一次我们要合并的是第i位和第i+4位,以此类推即可……
ps:本文中的“第i位”表示下标而不是排名。排名的话我会说“排名为i”

那么我们什么时候结束呢?很简单,当所有的排名都不同的时候我们直接退出就可以了,因为已经排好了。
显然这样排序的速度稳定在(log n)
基数排序
如果我们用快排的话,复杂度就是(n log^2 n) 还是太大。
这里我们用一波基数排序优化一下。在这里我们可以注意到,每一次排序都是排两位数,所以基数排序可以将它优化到O(n)级别,总复杂度就是(n log n)。
介绍一下什么是基数排序,这里就拿两位数举例
我们要建两个桶,一个装个位,一个装十位,我们先把数加到个位桶里面,再加到十位桶里面,这样就能保证对于每个十位桶,桶内的顺序肯定是按个位升序的,很好理解。
题目链接:https://www.luogu.org/recordnew/show/17637546
看代码:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> using namespace std; typedef long long LL; const LL maxn=1e6+50; char s[maxn];//存储输入的字符串 int y[maxn],x[maxn],c[maxn],sa[maxn],rk[maxn],height[maxn],wt[30]; int n,m; void putout(int x) { if(!x) { putchar(48); return ; } int l=0; while(x) wt[++l]=x%10,x/=10; while(l) putchar(wt[l--]+48); } void get_SA() { for(int i=1;i<=n;i++) ++c[x[i]=s[i]];//以字符的ASCII码为下标 //c数组是桶 x[i]是第i个元素的关键字 也就是存每个关键字有多少个 for(int i=2;i<=m;i++) c[i]+=c[i-1]; //做c的前缀和,我们就可以得出每个关键字最多是在第几名 for(int i=n;i>=1;i--) sa[c[x[i]]--]=i; // for(int i=1;i<=n;i++) cout<<sa[i]<<" "; // cout<<endl; // for(int i=1;i<=n;i++) sa[c[x[i]]--]=i; //为什么要从后往前呢? 因为我们按照单个字符比较大小 那么很有可能会有相同的字符 那么这些 //相同的字符怎么排名呢? 就先按照越在后的排名越往后的规则来 //前面已经说过 sa[i]说的是排第i的谁 /** 上面的代码已经按照单个字符排好序了 其实也就是按照了每个后缀数组的第一关键字排好序了 */ for(int k=1;k<=n;k<<=1)//这里是倍增 { int num=0; for(int i=n-k+1;i<=n;i++) y[++num]=i; //y[i]表示第二关键字排名为i 的数 第一关键字的位置 //第n-k+1到第n位是没有第二关键字的 所以排在最前面 for(int i=1;i<=n;i++) if(sa[i]>k) y[++num]=sa[i]-k; //排名为i的数 在数组中是否在第k位以后 //如果满足(sa[i]>k) 那么它可以作为别人的第二关键字 就把它的第一关键字的位置添加进y 就行了 //所以i枚举的是第二关键字的排名 第二关键字靠前的先入队 for(int i=1;i<=m;i++) c[i]=0; //初始化c桶 for(int i=1;i<=n;i++) ++c[x[i]]; //因为上一次循环已经算出了这次的第一关键字 所以直接加就行了 for(int i=2;i<=m;i++) c[i]+=c[i-1];//第一关键字排名为1~i的数有多少个 for(int i=n;i>=1;i--) sa[c[x[y[i]]]--]=y[i],y[i]=0; // for(int i=1;i<=n;i++) sa[c[x[y[i]]]--]=y[i],y[i]=0; // for(int i=1;i<=n;i++) cout<<sa[i]<<" "; // cout<<endl; //因为y的顺序是按照第二关键字的顺序来排的 //第二关键字靠后的,在同一个关键字桶中排名越靠后 //基数排序 swap(x,y); //所以现在y[i] 存的是第i个元素的关键字 //这里不用想太多 因为要生成新的x 时 要用到旧的 就把旧的复制下来 没别的意思 x[sa[1]]=1; num=1; for(int i=2;i<=n;i++) x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num; //因为sa[i]已经排好序了 所以可以按排名枚举 生成下一次的关键字 if(num==n) break; m=num; //这里不用那个122了 因为都有了新的编号 } // for(int i=1;i<=n;i++) putout(sa[i]),putchar(' '); cout<<sa[1]; for(int i=2;i<=n;i++) { cout<<" "<<sa[i]; } cout<<endl; } int main() { // cout<<(int)'0'<<endl; // cout<<(int)'z'<<endl; gets(s+1);//从1开始读入 n=strlen(s+1);//得到字符串的长度 m=122;//m表示字符个数 最小的数字0是48 最大的是字母z 是122 get_SA(); return 0; }
下面是经常和后缀数组一起用的height数组:
个人感觉,上面说的一大堆,都是为heightheight数组做铺垫的,heightheight数组才是后缀数组的精髓、
先说定义
ii号后缀:从ii开始的后缀
lcp(x,y)lcp(x,y):字符串xx与字符串yy的最长公共前缀,在这里指xx号后缀与与yy号后缀的最长公共前缀
height[i]height[i]:lcp(sa[i],sa[i−1])lcp(sa[i],sa[i−1]),即排名为ii的后缀与排名为i−1i−1的后缀的最长公共前缀
H[i]H[i]:height[rak[i]]height[rak[i]],即ii号后缀与它前一名的后缀的最长公共前缀
性质:H[i]⩾H[i−1]−1H[i]⩾H[i−1]−1
证明引自远航之曲大佬
update in 2019.3.28
在复习的时候我发现这里的证明有一个跳点,包括论文中的证明也有一点不严谨的地方
下面两处画红线的地方均没有证明"suffix(k+1)"与"i前一名的后缀之间的关系",实际上这两者之间的关系是:他们的lcp至少为h[i - 1] - 1。可以用反证法证明,在此不再赘述

能够线性计算height[]的值的关键在于h[](height[rank[]])的性质,即h[i]>=h[i-1]-1,下面具体分析一下这个不等式的由来。
我们先把要证什么放在这:对于第i个后缀,设j=sa[rank[i] – 1],也就是说j是i的按排名来的上一个字符串,按定义来i和j的最长公共前缀就是height[rank[i]],我们现在就是想知道height[rank[i]]至少是多少,而我们要证明的就是至少是height[rank[i-1]]-1。
好啦,现在开始证吧。
首先我们不妨设第i-1个字符串(这里以及后面指的“第?个字符串”不是按字典序排名来的,是按照首字符在字符串中的位置来的)按字典序排名来的前面的那个字符串是第k个字符串,注意k不一定是i-2,因为第k个字符串是按字典序排名来的i-1前面那个,并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。
这时,依据height[]的定义,第k个字符串和第i-1个字符串的公共前缀自然是height[rank[i-1]],现在先讨论一下第k+1个字符串和第i个字符串的关系。
第一种情况,第k个字符串和第i-1个字符串的首字符不同,那么第k+1个字符串的排名既可能在i的前面,也可能在i的后面,但没有关系,因为height[rank[i-1]]就是0了呀,那么无论height[rank[i]]是多少都会有height[rank[i]]>=height[rank[i-1]]-1,也就是h[i]>=h[i-1]-1。
第二种情况,第k个字符串和第i-1个字符串的首字符相同,那么由于第k+1个字符串就是第k个字符串去掉首字符得到的,第i个字符串也是第i-1个字符串去掉首字符得到的,那么显然第k+1个字符串要排在第i个字符串前面,要么就产生矛盾了。同时,第k个字符串和第i-1个字符串的最长公共前缀是height[rank[i-1]],那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rank[i-1]]-1。
到此为止,第二种情况的证明还没有完,我们可以试想一下,对于比第i个字符串的字典序排名更靠前的那些字符串,谁和第i个字符串的相似度最高(这里说的相似度是指最长公共前缀的长度)?显然是排名紧邻第i个字符串的那个字符串了呀,即sa[rank[i]-1]。也就是说sa[rank[i]]和sa[rank[i]-1]的最长公共前缀至少是height[rank[i-1]]-1,那么就有height[rank[i]]>=height[rank[i-1]]-1,也即h[i]>=h[i-1]-1。
void get_height(int len) { for(int i=1;i<=len;i++) { rk[sa[i]]=i; } int k=0; for(int i=1;i<=len;i++) { if(rk[i]==1) continue; if(k) --k; int j=sa[rk[i]-1]; while(j+k<=len&&i+k<=len&&s[i+k]==s[j+k]) ++k; height[rk[i]]=k; } return ; }