TG-WC2021 笔记

DAY1

DP

判断(a)的第(i)为(从低到高)是否为(1)

(1<<(-1))&a

把(a)第(i)位改成(1)

a|(a<<(i-1))

把(a)第(i)位改成(0)

a&(~(1<<i))

把(a)最后一个(i)去掉

a&(a-1)

关于四边形不等式

之前说区间(DP)死了，但是它可以被四边形不等式优化
关于它，不需完全会证明，只需知道三条引理：

• 1 若两个区间的vul值中，大区间的vul更大，那么vul满足四边形不等式
• 2 形如石子合并的区间DP转移方程，与vul有关的，也满足四边形不等式，另外，该定理只对min生效
• 3 记sij为fij的中间决策点，若f满足不等式，那么sij-1<=sij<=si+1j
  另：(LH)大佬给出了一个好方法检验

第一步，造一个较大的数据（但暴力能通过）
第二步，跑暴力，存好答案
第三步，跑不等式，存好答案
第四步，比对

看起来傻，实则很好

期望

求连续抛n个正面的期望次数

[E_x=E_{x-1}+frac{1}{2}*(1+E_x+1) ]

[E_x=2^{x+1}+2 ]

DAY2

网络流

没讲什么有趣的，不过重新学习了dicnic的证明方法，把牛顿迭代看了（摸鱼！）

字符串

扩展KMP

模板
结合一下马拉车和KMP，就是说，我们想求对于母串的所有后缀与模式串的最长前缀长度
首先不要被带进误区，对于母串我们正向扫，发现若一个点往后能扩展很长，就能覆盖后面的一些点
很像马拉车，我们发现，要是一个点在覆盖区，我们能向前找到一个点，像kmp一样，我们往前找，若新点和1号点一样，那么我们看看能不能把他往后延展的部分搬到前面来
这样就用马拉车的套路结合了kmp的操作

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
const ll N=2e7+30;
ll n,m,nxt[N],Nxt[N],ans1,ans2;
char c[N],s[N];

inline void get_nxt(){
	nxt[1]=m;
	for(ll r=0,mid=0,i=2;i<=m;i++){
		if(i<=r)nxt[i]=min(nxt[i-mid+1],r-i+1);
		while(i+nxt[i]<=m&&s[i+nxt[i]]==s[nxt[i]+1])++nxt[i];
		if(i+nxt[i]-1>r)mid=i,r=i+nxt[i]-1;
	}
}

inline void exkmp(){
	get_nxt();
	for(ll i=1,r=0,mid=0;i<=n;i++){
		if(i<=r)Nxt[i]=min(nxt[i-mid+1],r-i+1);
		while(i+Nxt[i]<=n&&c[i+Nxt[i]]==s[Nxt[i]+1])++Nxt[i];
		if(i+Nxt[i]-1>r)mid=i,r=i+Nxt[i]-1;
	}
}

int main(){
	cin>>c+1;
	cin>>s+1;
	n=strlen(c+1);
	m=strlen(s+1);
	exkmp();
	for(ll i=1;i<=m;i++)ans1^=i*(nxt[i]+1);
	for(ll i=1;i<=n;i++)ans2^=i*(Nxt[i]+1);
	printf("%lld
%lld",ans1,ans2);
}

SA

我们用一个长得很像分治的东西，将长为n的后缀们一半一半拆解，然后比较，用最小的两个举例
ab bc cd da as
12 23 34 41 15
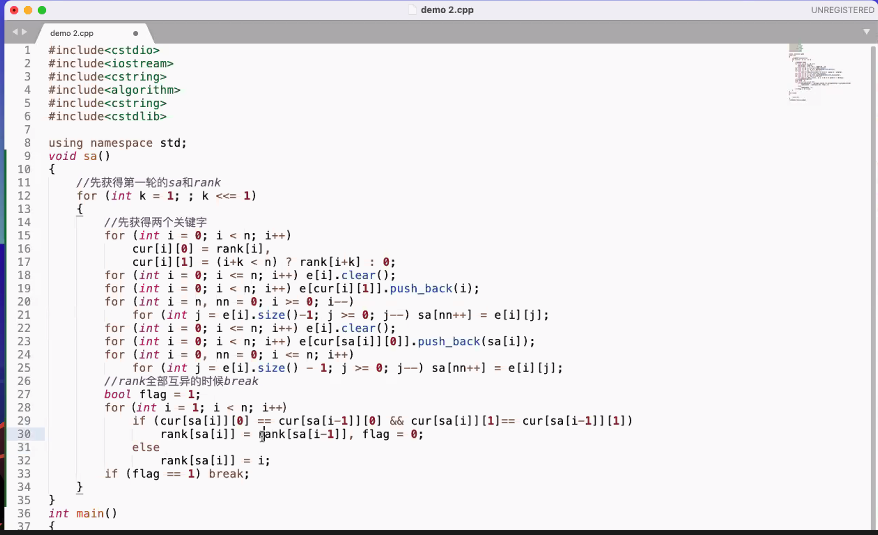
对他们基数排序，然后大的同理，贴个vector版伪代码

DAY3

树论

直径

树的所有直径叫交于一点