之前一直没怎么重视这一块,理解也是半知半解,现在想想还是得好好记下。
一.增量构造法
什么意思呢,简单来说就是把一个一个元素放进去又拿出来的过程
先上代码
//ass[]集合的数组
//num[]子集的数组 //n 集合的元素的个数 //cur 初始为0,代表着子集的元素的个数 void print_subset(int n, int *num, int cur) { for (int i = 0; i < cur; i++) {//输出目前子集 cout << ass[num[i]]; } cout << endl; int st = cur ? num[cur - 1]+1 : 0;//选择最小的未被选择的集合的一个元素 for (int i = st; i < n; i++) { num[cur] = i;//放入数组代替前面的num[cur] print_subset(n, num, cur + 1); } }
下面借用一张图,思路很清晰
注意:这里的1 2 3 4表示的是集合的下标,不是元素的值
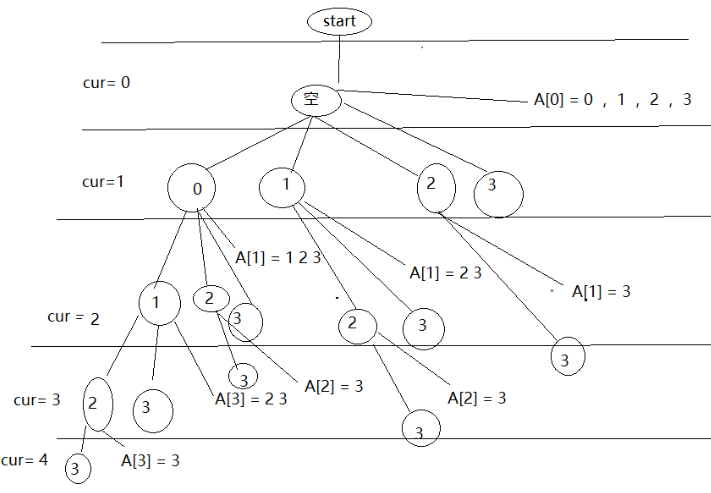
跟着算法的思路走一遍:
一开始,我们的子集为空,所以不需要输出,然后我们现在的子集元素个数cur为0,然后 我们拿 目前的 未被用到的 最小号元素放进去 子集,
OK,目前的状态是子集里面已经有了0号元素,保持这个状态我们接着往下走,
现在,我们的子集里面已经有了0号元素,可以输出0号,目前我们的子集元素个数cur为1,然后我们拿 目前的 未被用到的 最小号元素放进去 子集
OK,目前的状态是子集里面有了1号元素,保持这个状态我们接着往下走
………………………………以此类推,直到遇到第一个边界,也就是num[cur]==3 的时候,我们的集合的元素的个数只有4个,所以输出目前的子集后我们直接返回走,
目前我们回到了num[ cur==3 ]=3的状态,开始进入下一个循环,因为 i此时等于 4 ,不满足循环条件,接着返回上一个状态
目前我们回到了num[cur==2 ]=2的状态,开始进入下一个循环,
ok,此时我们的num[cur==2]=3,也就是说本来num[2]==2此时被代替成了3,这样子目前 子集就是 0 1 3,以此类推
这样我们的结果就是
0
0 1
0 1 2
0 1 2 3
0 1 3
0 2
0 2 3
0 3
1
1 2
1 2 3
1 3
2
2 3
3
二.位向量法
其实就是 放和不放 所得到的各种情况
例如 我目前的 集合的元素为 1 2 3 4 5
那我先拿出第一个元素 1
那我的子集要不要这个元素呢?有要和不要两种情况
那目前就有了两个子集 : 第一个子集 为 空
第二个子集 为 1
再拿出第二个元素 2:
那我的子集要不要这个元素呢?有要和不要两种情况,而第一个元素 1 要和不要也有两种情况,于是目前就有了四种情况
那目前就有了四个子集: 第一个子集为空
第二个子集为 1
第三个子集为 2
第四个子集为 1 2
以此类推,我们就会得到所有子集的情况
下面给出代码:
#include<iostream> using namespace std; //ass[]集合的元素 //num[]子集的数组 //n 集合的元素的个数 //cur 初始为0,代表着集合元素的下标 void print_subset(int n, int *num, int cur) { if (cur == n) { for (int i = 0; i < cur; i++) { if (num[i]) { cout << ass[i]; } } cout << endl; return; } num[cur] = 1;//要ass[cur]这个元素 print_subset(n, num, cur + 1); num[cur] = 0;//不要ass[cur]这个元素 print_subset(n, num, cur + 1); }
三 . 二进制法
这个应该是最难懂的,需要先学习二进制的概念和各种位运算符,不然没必要往下看
如果你已经懂了,那接着往下说。
要知道,二进制中,只有 1 和 0 两个数字,那我们就把 1代表有这个元素,0代表没有这个元素
假如我们的集合为{7 , 8 ,9}
那么子集用二进制表示就是这样
001 010 011 100 101 110 111 如此,我们知道有9种情况
这代表着什么呢?
(它的代表是反向的)
例如 001代表着 有 7 这个元素 ,没有 8 和 9 元素 ,
101代表着 有7和 9元素,没有 8元素
1 1 1 代表着全部都有
那好,我们知道它是怎么代表的,那又有什么用呢?
接着往下看:
首先我们要知道集合元素的个数,这里假设为 N
那我们再看这样一个式子 (1<<N)-1
什么意思呢?我们知道数组是从0开始的,比如我们的集合有3个元素,放在数组里面,它们的下标就是 0 1 2
那么我们可以知道N==3,所以我们 (1<<N)-1==(1000 - 0001)(二进制)==111,看!“ 111 ” 那它不就代表着集合全部的元素都有吗!
那么我们接下来不断的让 111 减去 001也就是 十进制的 1 ,那么就有了 110 101 011 010 001 000
所以,下面给出枚举的代码:
//ass[]集合的元素 //n 集合的元素的个数 void print_subset(int n,int *ass) { for (int i = (1 << n) - 1; i > 0; i--) {//子集目前的二进制状态 for (int j = 1; j <= n; j++) { if (i&j) {//如果子集的二进制目前的j位为1,那就输出 cout << ass[j - 1]; } } cout << endl; }