（基本数论）素数筛选与判断

1、朴素判断素数

这种方法就是将给出的数判断能否找到处1以及它本身以外的因数。

代码样例

#include <bits/stdc++.h>
using namespace std;

bool f(int n){
    for(int i=2; i*i <= n; i++){
        if(n%i == 0)
            return 0;
    }
    return 1;
}

int main(){
    int n;
    cin >> n;
    if(f(n))
        cout << "Yes" << endl;
    else
        cout << "No" << endl;
}

2、埃氏筛法

埃氏筛法就是从2开始筛掉2的倍数（必须从2倍开始）往下依次进行。

代码样例

#include <bits/stdc++.h>
using namespace std;

const int 1E6;
bool book[maxn};

void Is_not_prime(int n){
    memset(book,false,sizeof(book));
    book[0]=true;
    book[1]=true;
    for(int i=2; i <= n; i++){
        if(!book[i]){
            for(int j=i+i; j <= n; j+=i)
                book[j]=true;
        }
    }
}

int main(){
    int n,m;
    cin >> n >> m;
    Is_not_prime(n);
    for(int i=1; i<= m; i++){
        int x;
        cin >> x;
        if(!book[x]);
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}

3、欧拉筛法

欧拉筛法其实是对埃氏筛法的优化，在埃氏筛法中有多于3个因数的合数会被重复筛一次这样增加了不必要的操作。欧拉筛则可以弥补这一不足之处（见下图）

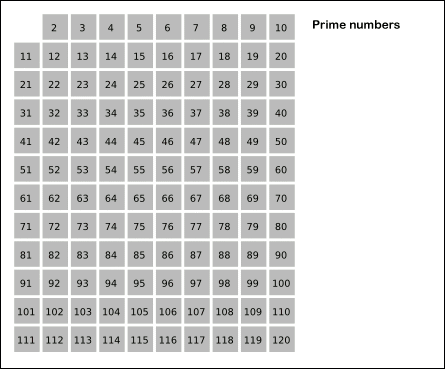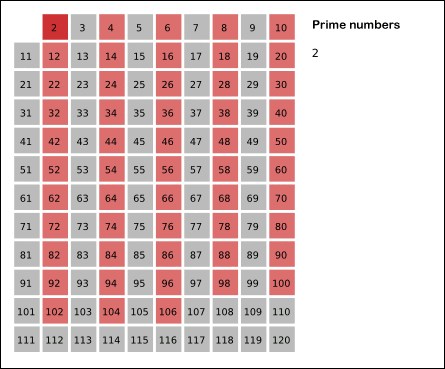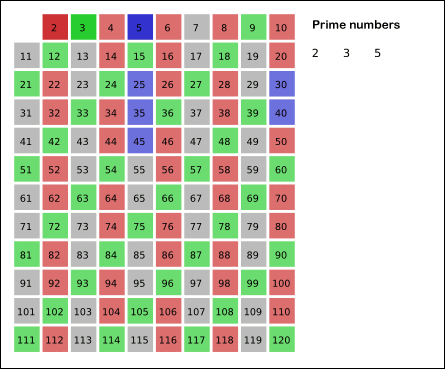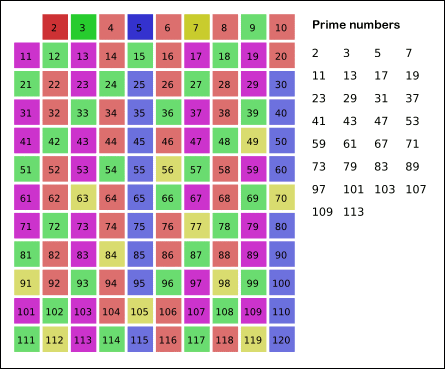
代码样例

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e7+10;
bool book[maxn];
int prime[maxn];
int cnt;

void Init(int n){
    cnt = 0;
    memset(book,0,sizeof(book));
    book[1] = 1;
    for(int i = 2; i <= n; i++){
        if(book[i]==0){
            prime[cnt++] = i;
        }
        for(int j = 0; j < cnt && prime[j]*i <= n; j++){
            book[i*prime[j]] = 1;
            if(i%prime[j] == 0)
                break;
        }
    }
}

int main(){
    int n,m;
    cin>>n>>m;
    Init(n);
    for(int i = 0;i < m; i++){
        int x;
        cin>>x;
        if(book[x]==0)
            cout<<"Yes"<<endl;
        else
            cout<<"No"<<endl;
    }
    return 0;
}

4、Miller_Rabin判素数

（这里目前未搞懂）

算法过程

1：先判断n是不是小于2，是的话就返回0。

2：再判断n是不是等于2，是的话就返回1。

3：再判断n是不是偶数及(n&1)==0,是的话返回0。

4：令p-1 = 2^t*u,此时p是奇数，u是奇数。

5：随机取一个a，a∈(1,n) a = rand()%n-1 + 1;。

6: 因为n-1 = u * 2^t，所以a(n-1)=a^(u * 2^t)=(au)⁽²t),令 x = (a^u)%n

7: 然后是t次循环，每次循环都让y = (x * x)%n，x=y,这样t次循环之后x=a^(u * 2^t)=a(n-1)了。

8: 因为循环的时候y=(x * x)%n，且x肯定是小于n的，正好可以用二次探测定理。

9: 如果(x^2)%n1，也就是y等于1的时候，假如n是素数，那么x1||x==n-1，如果x!=1&&x!=n-1，那么n肯定不是素数了，返回false。

10: 运行到这里的时候x=a^(n-1)，根据费马小定理，x!=1的话，肯定不是素数，返回false。

11: 因为Miller-Rabin得到的结果的正确率为 75%，所以要多次循环步骤4~8来提高正确率。

12: 循环多次之后还没返回，那么n肯定是素数，返回true。

• 费马小定理定义：设P是一个素数，a是一个正整数，且GCD(a,p)==1,则
  [{a^{p - 1}} equiv 1left( {modp} ight) ]
  注意：逆定理不成立!

代码样例

#include<bits/stdc++.h>
using namespace std;
#define ll unsigned long long

ll mod_exp(ll a,ll b,ll n){
    ll res = 0;
    while(b){
        if(b&1)
            res = (res + a)%n;
        a = (a+a)%n;
        b>>=1;
    }
    return res;
}

ll mod_pow(ll a,ll b,ll n){
    ll res = 1;
    while(b){
        if(b&1)
            res = mod_exp(res,a,n);
        a = mod_exp(a,a,n);
        b>>=1;
    }
    return res;
}

bool miller_rabin(ll n){
    if(n==2)
        return true;
    if(n<=1||!(n&1))
        return false;
    ll i,j,t,u;
    t = 0;
    u = n-1;
    while(u&1==0)// n-1 化成 u*2^t u为奇数；
    {
        t++;
        u>>1;
    }
    for(i = 0;i < 10; i++){
        ll a = rand()%(n-1)+1;
        ll x = mod_pow(a,u,n);
        for(j = 0;j < t; j++){
            ll y = mod_exp(x,x,n);
            if(y==1&& x!=1 && x!=n-1)
                return false;
            x = y;
        }
        if(x!=1)
            return false;
    }
    return true;
}

int main(){
    ll i,j,t,n;
    scanf("%llu",&t);
    while(t--){
        scanf("%llu",&n);
        for(i = 1;i < n;i++){
            if(miller_rabin(i)&&miller_rabin(n-i)){
                printf("%llu %llu
",i,n-i);
                break;
            }
        }
    }
    return 0;
}

5、简单区间筛选素数

代码样例

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1e6+10;
bool book[maxn];
int a[maxn];

void Init(int n){
    memset(book,0,sizeof(book));
    book[1] = 1;
    a[1] = 0;
    for(int i = 2; i <= n; i++){
        if(book[i]==0){
            a[i] = a[i-1]+1;
            for(int j = i+i; j <= n; j+=i){
                book[j] = 1;
            }
        }
        else
            a[i] = a[i-1];
    }
}

int main(){
    int n,m;
    cin>>n>>m;
    Init(m);
    for(int i = 0; i < n; i++){
        int l,r;
        cin>>l>>r;
        if(r>m||l<1)
            cout<<"Crossing the line"<<endl;
        else{
            cout<<a[r]-a[l-1]<<endl;
        }
    }
    return 0;
}

6、增强版区间筛选素数

代码样例

/*
注意，j=max(2ll,(l+i-1)/i)*i的意思：
(l+i-1)/i表示大于等于l的i的倍数的最小值。
2则是普遍的i的倍数的最小值，一定不能小于2。
*/
#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e6+10;
bool vis[maxn];
bool book[maxn];
typedef long long ll;

int main(void){
    ll l,r;
    cin>>l>>r;
    for(ll i = 2;i*i <= r;i++){
        if(vis[i]==0){
            for(ll j = i; j*j <= r;j += i)
                vis[j]=1;
            for(ll j=max(2ll,(l+i-1)/i)*i;j <= r;j += i) //(a+i-1)/i 得到最接近a的i的倍数，最低是i的2倍，然后筛选
                book[j-l]=1;
        }
    }
    int ans = 0;
    for(int i = 0;i <= r-l;i++)
        if(book[i]==0)
            ans++;
    printf("%d
",ans);
return 0;
}