0.PTA得分截图

1.本周学习总结
1.1 总结图内容
图存储结构
邻接矩阵
图的邻接矩阵是一种采用邻接矩阵数组表示顶点之间相邻关系的存储结构。

邻接矩阵特点:
- 图的邻接矩阵表示是唯一的。
- 对于含n个顶点的图,采用邻接矩阵存储时,无论是有向图还是无向图,也无论边数多少,其储存空间都未O(n^2),所以适合存储稠密图。
- 无向图的邻接矩阵数组一定是对称矩阵,在存放邻接数组时可以只存上三角部分的元素。
- 对于无向图,邻接矩阵数组的第i行或第i列非零元素,非∞元素的个数是顶点i的度。
- 对于有向图,邻接矩阵数组的第i行(或第i列)非零元素,非∞元素的个数是顶点i的出度(或入度)。
- 在邻接矩阵中,判断图中两个顶点之间是否有边或者求两个顶点之间边的权的执行时间为O(1)。
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
} MGraph; //图的邻接矩阵表示类型
void CreateMGraph(MGraph& g, int n, int e)
{
int i, j, a, b;
for (i = 1; i <= n; i++) //矩阵初始化
for (j = 1; j <= n; j++)
g.edges[i][j] = 0; //无权图矩阵赋值0或1,有权图赋值0,∞,权
for (i = 0; i < e; i++) //输入边
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1; //无向图需要对称赋值
}
g.e = e;
g.n = n;
}
邻接表
图的邻接表是一种顺序与链式存储相结合的存储方法。
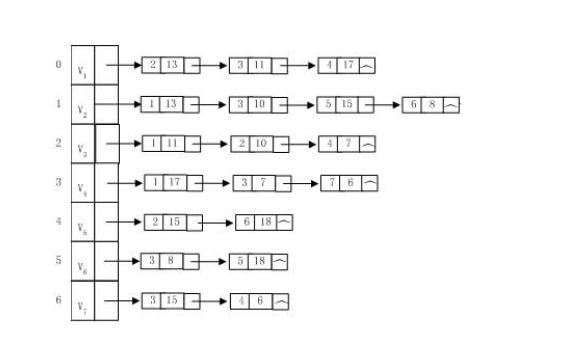
邻接表特点:
- 邻接表的表示不唯一,取取决于建立邻接表的算法以及边的输入次序。
- 对于n个顶点e条边的无向图,其邻接表有n个头结点和2e个边结点;对于n个顶点e条边的有向图,其邻接表有n个头结点和e个边结点。因此邻接表适合稀疏图。
- 对于无向图,邻接表中顶点i对应的第i个单链表的边结点数目是顶点i的度。
- 对于有向图,邻接表中顶点i对应的第i个单链表的边结点数目是顶点i的出度。顶点i的入度为邻接表中所有adjvex域值为i的边结点数目。
- 在邻接表中,查找顶点i关联的所有边是非常快速的,所以在需要提取某个顶点的所有邻接点的算法中通常采用邻接表。
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
void CreateAdj(AdjGraph*& G, int n, int e)
{
ArcNode* p, * q;
int i,a,b;
G = new AdjGraph;
for (i = 1; i <= n; i++)
{
G->adjlist[i].firstarc = NULL; //头结点初始化
}
for (i = 1; i <= e; i++)
{
cin >> a >> b; //输入边
/*无向图需要双向赋值*/
p = new ArcNode;
q = new ArcNode;
p->adjvex = b;
q->adjvex = a;
p->nextarc = G->adjlist[a].firstarc;
G->adjlist[a].firstarc = p;
q->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = q;
}
G->n = n;
G->e = e;
}
图遍历及应用
深度优先遍历(DFS)
DFS的过程是从图中的某个初始顶点v出发,首先访问v,然后选择一个与顶点v相邻且没被访问过的顶点w,以顶点w为初始顶点,再从它出发进行DFS,直到所有顶点被访问。
当以邻接矩阵表示图时,DFS时间复杂度为O(n^2);当以邻接表表示图时,DFS时间复杂度为O(n+e),n为顶点数e为边数。
/*邻接矩阵表示图*/
void DFS(MGraph g, int v)
{
int i;
visited[v] = 1; //已访问顶点
cout << v; //输出初始顶点
for (i = 1; i <= g.n; i++)
{
if (g.edges[v][i] && !visited[i]) //对相邻且为访问过的顶点递归
DFS(g, i);
}
}
/*邻接表表示图*/
void DFS(AdjGraph* G, int v)
{
ArcNode* p;
visited[v] = 1; //已访问顶点
cout << v; //输出初始顶点
p = G->adjlist[v].firstarc; //指向边结点
while (p!=NULL) //遍历但链表
{
if (visited[p->adjvex] == 0) //对未访问过的顶点递归
DFS(G, p->adjvex);
p = p->nextarc;
}
}
广度优先遍历(BFS)
BFS的过程是先访问初始顶点v,接着访问顶点v的所有未被访问过的邻接点,借助队列储存这些邻接点,再以队列中顶点的次序访问每个顶点的所有未被访问过的邻接点,直到所有顶点被访问。
当以邻接矩阵表示图时,BFS时间复杂度为O(n^2);当以邻接表表示图时,BFS时间复杂度为O(n+e),n为顶点数e为边数。
/*邻接矩阵表示图*/
void BFS(MGraph g, int v)
{
queue<int>q; //定义队列q
int i, j;
cout << v; //输出起始顶点
visited[v] = 1; //已访问顶点
q.push(v); //顶点加入队列
while (!q.empty()) //队列不空时循环
{
i = q.front(); //出队顶点i
q.pop();
for (j = 1; j <= g.n; j++)
{
if (g.edges[i][j] && !visited[j]) //顶点i的邻接点入队并输出
{
cout << " " << j;
visited[j] = 1;
q.push(j);
}
}
}
}
/*邻接表表示图*/
void BFS(AdjGraph* G, int v)
{
queue<int>q; //定义队列q
ArcNode* p;
int d;
cout << v; //输出起始顶点
visited[v] = 1; //已访问顶点
q.push(v); //顶点加入队列
while (!q.empty()) //队列不空时循环
{
d = q.front(); //出队顶点d
q.pop();
p = G->adjlist[d].firstarc; //顶点d的边结点
while (p)
{
if (visited[p->adjvex] == 0) //每个边结点入队并输出
{
cout << " " << p->adjvex;
visited[p->adjvex] = 1;
q.push(p->adjvex);
}
p = p->nextarc;
}
}
}
判断图的连通性
可以通过DFS、BFS或拓扑排序判断图的连通性,若是连通图则所有顶点都会被访问。
/*判断图g是否连通*/
bool IsConnect(AdjGraph g)
{
int i;
for(i=0;i<g.n;i++) //初始化visited[]
visited[i]=0;
DFS(g,0); //或BFS(g,0);
for(i=0;i<g.n;i++) //判断是否每个顶点都被访问过
if(!visited[i])
return false;
return true;
}
/*深度优先遍历非连通图*/
void DFS1(Graph g)
{
for(int i=0;i<g.n;i++)
if(!visited[i]) //对未访问过的顶点进行DFS
DFS(g,i);
}
/*广度优先遍历非连通图*/
void BFS1(Graph g)
{
for(int i=0;i<g.n;i++)
if(!visited[i]) //对未访问过的顶点进行BFS
BFS(g,i);
}
查找图路径
采用深度优先遍历可以查找顶点u到v的简单路径,所谓简单路径是指路径上顶点不重复。
void FindPath(AdjGraph G,int u,int v,int path[],int d) //d表示路径长度初始为-1
{
int w,i;
ArcNode *p;
visited[u]=1;
d++; //路径长度d增1,顶点u加入路径
path[d]=u;
if(u==v&&d>=0) //找到一条路径
{
for(i=0;i<=d;i++)
cout<<path[i];
cout<<endl;
return;
}
p=G->adjlist[u].firstarc; //p指向u的第一个邻接点
while(p)
{
w=p->adjvex;
if(!visited[w]) //w未被访问则递归访问
FindPath(G,w,v,path,d)
p=p->nextarc;
}
/*删除return,加上visited[u]=0恢复环境可以找出图中所有最短路径*/
}
寻找最短路径
根据BFS层层向外搜索的特点,可以找到顶点u到顶点v的一条最短路径
void ShortPath(AdjGraph G,int u,int v)
{
定义队列q,visited[MAXV];
初始化visited为0;
顶点u入队;
while 队列不空
{
出队顶点w;
if(w==v)
输出路径;
p=G->adjlist[w].firstarc;
while(p)
将w的未访问过的邻接点入队;
}
}
最小生成树相关算法及应用
Prim算法
Prim算法步骤:
(1)初始化U={v},以v到其他顶点的所有边为候选边。
(2)重复以下步骤(n-1)次,使得其他(n-1)个顶点被加入到U中。
1.从候选边中找权最小的顶点加入TE,将该顶点k加入U中;
2.考查当前V-U中的所有顶点j修改候选边,若(k,j)的权小于原来顶点j关联的候选边,则用(k,j)代替后者作为候选边。

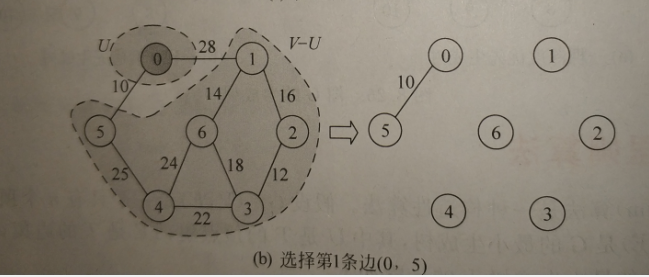
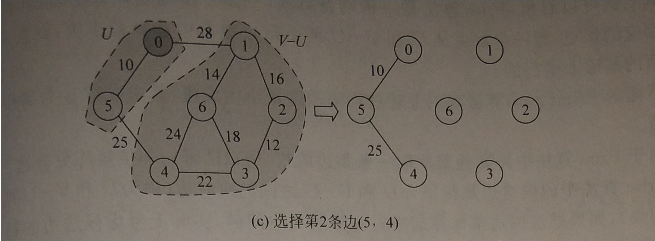
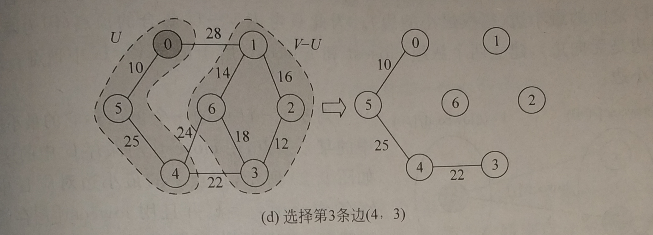
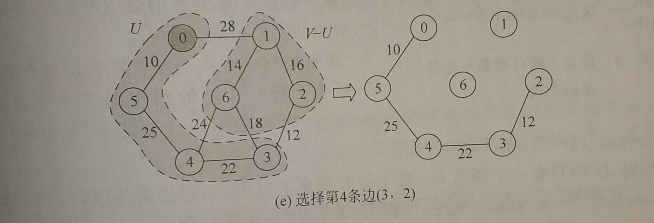
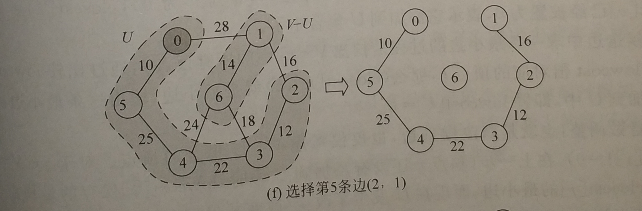

建立两个数组closest和lowcost用于记录V-U中顶点j到U中顶点的最小边。如最小边表示为(closest[j],j),对应权为lowcost[j],lowcost[i]=0表示顶点i已被选,即i∈U。
Prim算法时间复杂度为O(n^2),只和图中顶点数有关,因此适合用于稠密图求最小生成树。
void Prim(MGraph g, int v)
{
定义 lowcost[MAXV], closest[MAXV], k;
初始化lowcost[]和closest[];
顶点v加入U;
for i = 1 to i < g.n do //找(n-1)个顶点
{
找离U最近的顶点k;
k加入U;
for j = 1; j <= g.n; j++ do//调整顶点j
if (lowcost[j] != 0 && g.edges[k][j] < lowcost[j])
{
lowcost[j] = g.edges[k][j];
closest[j] = k; //调整lowcost和closest
}
}
}
Kruskal算法
Kruskal算法步骤:
(1)置U的初值为V,TE的初值为空集。
(2)将图G中的边按照权从小到大的顺序依次选取,若选取的边未使生成树T形成回路,则加入TE,否则舍弃,直到TE包含(n-1)条边。

设置数组vest记录顶点所在连通分量编号,当连通分量编号相同则表示加入后会形成回路,不能加入;否则加入后不会出现回路,可以加入,然后将两个顶点所在连通分量中所有顶点的连通分量编号改为相同。
设置结构体数组E存放所有边,并且权值按从小到的顺序排列。
边采用堆排序的Kruskal算法时间复杂度为O(eloge),只和图中边数有关,因此适合用于稀疏图求最小生成树。
/*改进的算法*/
void Kruskal(MGraph g)
{
定义并查集t[MAX],结构体数组E[MAX];
生成g的边集E;
采用堆排序对E中权递增排序;
MAKE_SET(E,g.n); //初始化并查集
while 边数k小于n do
{
取一条边的头尾顶点u1,u2;
sn1=FIND_SET(t,u1); //找到u1所属于的集合
sn2=FIND_SET(t,u2); //找到u2所属于的集合
if sn1不等于sn2 //两个顶点属于不同的集合,该边是最小生成树的一条边
{
输出边,边数k++;
UNION(t,u1,u2); //u1,u2顶点合并
}
扫描下一条边;
}
}
最短路径相关算法及应用
Dijkstra算法
Dijkstra算法步骤:
(1)初始时,S={v},U={除v以外其他顶点}。
(2)从U中选择一个到v最近的顶点u,把u加入S。
(3)以顶点u为新考虑中间点,修改源点v到U中所有顶点的最短路径长度。
(4)重复步骤(2)(3),直到S包含所有的顶点。

定义数组dist记录每个顶点到v的最短距离,如dist[j]表示源点v到j的最短路径长度。数组path记录最短路径,如path[j]表示源点v到j最短路径上j的前一个顶点。数组S记录已访问过的顶点。
Dijkstra算法的时间复杂度为O(n^2),n为图中顶点个数。
void dijkstra(MGraph g,int v)
{
定义dist[MAXV],path[MAXV],S[MAXV];
初始化dist,path,s;
源点v放入S;
for i=0 to i<g.n-1 do
{
选取U中最小路径长度顶点u;
d顶点u加入S;
for j=0 to j<g.n do //修改U中顶点的最短路径
if(S[j]==0&&g.edges[u][j]<INF&&g.edges[u][j]+dist[u]<dist[j])
{
dist[j]=g.edges[u][j]+dist[u];
path[j]=u;
}
}
输出最短路径;
}
Floyd算法
Floyd算法步骤:
A[i][j]为顶点i到d顶点j的最短路径的距离,对于每一个顶点k,判断A[i][k]+A[k][j]<A[i][j]是否成立,若成立则从i到k再到j的路径比i直接到j的路径短A[i][j]=A[i][k]+A[k][j],当遍历完所有顶点k就得到了最短路径。
定义二维数组A存放当前顶点之间的最短路径长度,如A[i][j]表示当前i到j的最短路径长度。
定义二维数组path存放最短路径,如path[i][j]存放i到j最短路径上j的前一个顶点。
Floyd算法时间复杂度O(n^3),n为图中顶点数。
void Floyd(MGraph g)
{
定义A[MAXV][MAXV],path[MAXV][MAXV];
初始化A,path;
for(k=0;k<g.n;k++)
for(i=0;i<g.n;i++)
for(j=0;j<g.n;j++)
A[i][j]=min{A[i][j],A[i][k]+A[k][j]}; //修改最短路径
输出最短路径;
}
拓扑排序、关键路径
拓扑排序
在一个有向图中找一个拓扑序列的过程称为拓扑排序。
拓扑排序步骤:
(1)在有向图中选择一个入度为0的顶点输出。
(2)从图中删除该顶点和从该顶点出发的边。
(3)重复步骤(1)(2),直到图中不存在入度为0的顶点。
拓扑排序可以判断图是否存在回路,若输出拓扑序列包含图中所有顶点则不存在回路,否则图存在回路。
拓扑排序的时间复杂度为O(n+e),n为图中顶点数e为边数。
void TopSort(AdjGraph* G)
{
定义栈st,Top[MAXV];
入度置初值0;
求所有顶点入度;
将所有入度为0顶点入栈;
while 栈不空 do
{
出栈一个顶点i,并输出;
顶点i的邻接点入度减1;
if 顶点入度等于0
入栈;
找下一个邻接点;
}
/*可以定义cnt记录输出顶点数,若cnt不等于g.n则图存在回路*/
}
关键路径
- 在AOE网中,从源点到汇点的最长路径称为关键路径。
- AOE网中的顶点称为事件,边称为活动。
- 事件v的最早开始时间ve(v)等于x到v的最长路径。
- 事件v的最迟开始时间vl(v)等于ve(y)与v到汇点y的最长路径之差。
- 活动a的最早开始时间e(a)等于ve(j),a=<j,k>。
- 活动a的最迟开始时间l(a)等于vl(k)-e(a),a=<j,k>。
- 最早开始时间等于最迟开始时间的活动称为关键活动,由关键活动连成的路径就是关键路径。
1.2.谈谈你对图的认识及学习体会。
- 图属于非线性结构,元素之间的关系是多对多的关系,实际问题中很多都可以运用图来描述。
- 图可以使用邻接矩阵或邻接表存储,需要具体看所求问题特点和数据特点。
- 学习图先要了解图的基本术语,然后是图的创建、遍历等。
- 图中有最小生成树和最短路径两个概念,求最小生成树的算法是Prim、Kruskal,求最短路径的算法是Dijkstra,Floyd,需要注意区分两者的概念和异同点。
- 拓扑排序只针对有向图而言,有向图可以表示顶点之间的先后关系,而输出的拓扑序列一般是不唯一的。
- 经过图一章的学习,特别是图中Prim、Kruskal、Dijkstra、Floyd等算法的学习,让我感觉到算法有趣的同时也挺难理解和掌握的。
- 图的实际应用中也时常使用到前几章所学的内容,如栈队列,树等,综合性较强。
2.阅读代码:
2.1 题目及解题代码

class Solution {
public int maxDistance(int[][] grid) {
int[] dx = {0, 0, 1, -1};
int[] dy = {1, -1, 0, 0};
Queue<int[]> queue = new ArrayDeque<>();
int m = grid.length, n = grid[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
queue.offer(new int[] {i, j});
}
}
}
boolean hasOcean = false;
int[] point = null;
while (!queue.isEmpty()) {
point = queue.poll();
int x = point[0], y = point[1];
for (int i = 0; i < 4; i++) {
int newX = x + dx[i];
int newY = y + dy[i];
if (newX < 0 || newX >= m || newY < 0 || newY >= n || grid[newX][newY] != 0)
continue;
grid[newX][newY] = grid[x][y] + 1;
hasOcean = true;
queue.offer(new int[] {newX, newY});
}
}
if (point == null || !hasOcean)
return -1;
return grid[point[0]][point[1]] - 1;
}
}
2.1.1 该题的设计思路
采用多源BFS的方法,一般BFS是从单个源点v开始遍历,该方法改为多个源点同时进行BFS。先把所有的陆地都入队,然后从各个陆地同时开始一层一层的向海洋扩散,那么最后扩散到的海洋就是最远的海洋。
1代表陆地,0代表海洋,每次扩散周围4块海洋。
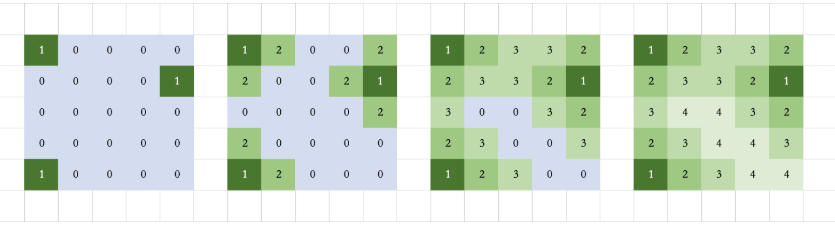
时间复杂度O(n2),空间复杂度O(n2)。
2.1.2 该题的伪代码
定义队列queue;
所有的陆地入队;
while 队列不空 do
{
取队头元素point;
for i=0 to i<4 do
将各方向的海洋入队,将距离保存在矩阵中; //保存距离就不需要再标志已访问
}
if 没有陆地或者没有海洋
return -1;
返回最后一次遍历到的海洋的距离;
2.1.3 运行结果
2.1.4分析该题目解题优势及难点。
- 题目没有用求出每个海洋到陆地的距离然后找出最大值的方法,而是使用多源的BFS,在多个源点层层搜索的过程中最后访问的海洋就是最远的。
- 时间效率上比采用Floyd算法更高。
2.2 题目及解题代码

class Solution {
public:
int findTheCity(int n, vector <vector<int>> &edges, int distanceThreshold) {
vector <vector<int>> D(n, vector<int>(n, INT_MAX));
for (auto &e : edges)
{
D[e[0]][e[1]] = e[2];
D[e[1]][e[0]] = e[2];
}
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
if (i == j || D[i][k] == INT_MAX || D[k][j] == INT_MAX)
continue;
D[i][j] = min(D[i][k] + D[k][j], D[i][j]);
}
int ret;
int minNum = INT_MAX;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (i != j && D[i][j] <= distanceThreshold) {
cnt++;
}
}
if (cnt <= minNum) {
minNum = cnt;
ret = i;
}
}
return ret;
}
};
2.2.1 该题的设计思路
使用Floyd算法求出各个城市到其它城市的距离,保存在矩阵D[n][n]中。
遍历D[n][n],统计各个城市在距离不超过 distanceThreshold 的情况下,能到达的其它城市的数量。
返回能到达其它城市最少的城市 ret。
时间复杂度O(n3)空间复杂度O(n2)。
2.2.2 该题的伪代码
定义二维D向量,并初始化各个城市间距离为INF;
根据edges[][]初始化D[][];
for k=0 to k<n do
for i=0 to i<n do
for j=0 to j<n do
D[i][j] = min(D[i][k] + D[k][j], D[i][j]);
for i=0 to i<n do
{
cnt=0;
for j=0 to j<n do
if i!=j&&D[i][j]<distanceThreshold
cnt++;
找出最小cnt对应的标号ret;
}
return ret;
2.2.3 运行结果
2.2.4分析该题目解题优势及难点。
- 要先理解题目的意思把邻居最少这各问题转成求最短路径问题,。
- 该做法求出了图中每对顶点的最短路径,再根据阈值选择最短路径编号。
2.3 题目及解题代码

class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] indegrees = new int[numCourses];
List<List<Integer>> adjacency = new ArrayList<>();
Queue<Integer> queue = new LinkedList<>();
for(int i = 0; i < numCourses; i++)
adjacency.add(new ArrayList<>());
for(int[] cp : prerequisites) {
indegrees[cp[0]]++;
adjacency.get(cp[1]).add(cp[0]);
}
for(int i = 0; i < numCourses; i++)
if(indegrees[i] == 0) queue.add(i);
while(!queue.isEmpty()) {
int pre = queue.poll();
numCourses--;
for(int cur : adjacency.get(pre))
if(--indegrees[cur] == 0) queue.add(cur);
}
return numCourses == 0;
}
}
2.3.1 该题的设计思路
本题可约化为课程安排图是否是有向无环图。即课程间规定了前置条件,但不能构成任何环路,否则课程前置条件将不成立。
统计课程安排图中每个节点的入度,生成入度表,根据拓扑排序判断有无环。
时间复杂度O(n+e),空间复杂度O(n+e)。
2.3.2 该题的伪代码
定义队列queue;
初始化入度;
入度为0的顶点入队;
while 队列不空 do
{
出队顶点pre;
numCourses--;
if 入度为0
入队;
}
返回numCourses == 0 判断课程是否可以成功安排;
2.3.3 运行结果
2.3.4分析该题目解题优势及难点。
- 理解题目中课程安排是就要求有向无环图进行拓扑排序。
- 根据拓扑排序判断是否是有向无环图。