排序算法---希尔排序

　　对于大规模的乱序数组进行插入排序，速度会很慢，因为他们只交换相邻的元素。因此元素只能一点点的从数组的一端移动到数组的另一端。

　　希尔排序就是为了加快速度简单的改进了插入排序，交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组将局部有序的数组排序

希尔排序

　　希尔排序的思想是使数组中任意间隔为h的元素都是有序的。这样的数组被称为h有序数组。换句话说，一个h有序数组就是h个相互独立的有序数组编织在一起组成的一个数组。（见下图1.1）在进行排序时，如果h很大，我们就能将元素移动到很远的地方，为实现更小的h有序创造方便。用这种方式，对于任意以1为结尾的h序列， 我们都能够将数组排序。这就是希尔排序。

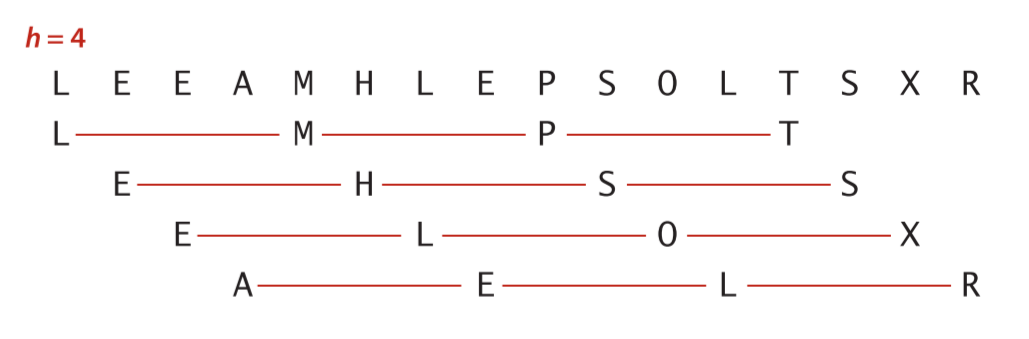
　　　　　　　　图1.1一个h有序数组即一个由h个有序子数组组成的数组

下面是算法图解：

首先看一个3-排序的图：第一行为输入，后面每行都是一次排序后的结果。灰色为未调整位置的元素

因为是3-排序，所以 红黄蓝各为一个独立数组

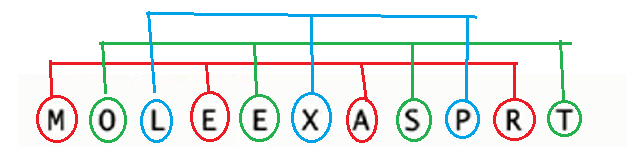
第一次排序 i=3 j=1 j-h =0 EM两个元素进行排序

第二次排序 i=4 j = 4 j-h = 1 O E 两个元素进行排序

第三次排序 i=5 j = 5 j-h = 2 X L 两个元素排序 X自己和自己交换位置

第四次i = 6 j = 6 j-h = 3 A M两个元素排序 

　　j = 3 j-h = 0 A E 两个元素进行排序 最终形成A E M 的顺序

后面以此类推即可

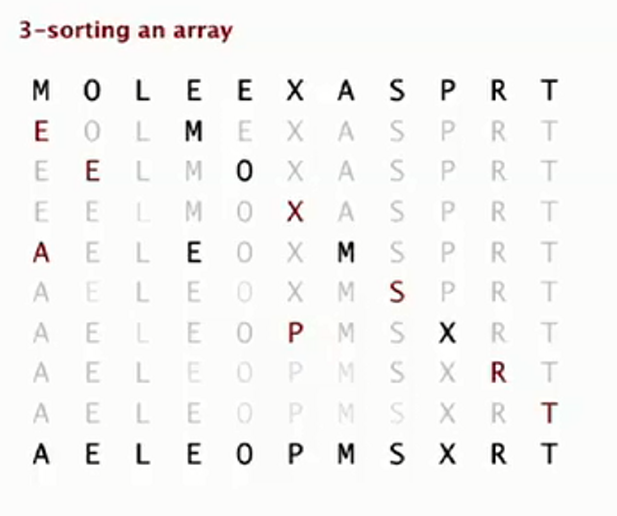
 下面在来一个完成的示例

输入

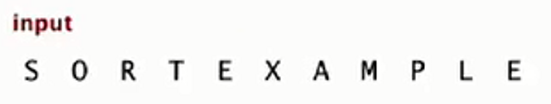
递增序列2^k-1 即 1，3，7

第一轮 进行7-排序

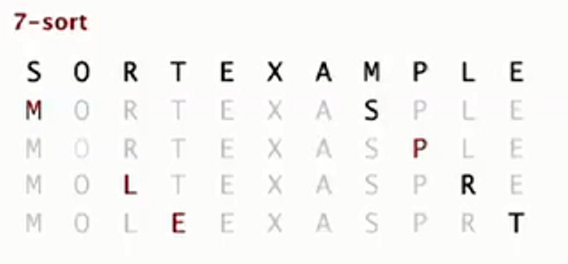
第二轮 3排序

最后进行1-排序

 下面是算法实现

package sort;

public class Shell {
    public static void sort(Comparable[] a) {
        int N = a.length;
        int h = 1;

        while (h < N / 3) h = h * 3 + 1;//1,4,13,40,121 设置h数组的大小3^k+1
        //设置为2的幂次递增 是不可以的
        while (h < N /2) h = h*2;
        while (h >= 1) {
            for (int i = h; i < N; i++) {//每次循环从第一个h开始，依次向前
                for (int j = i; j >= h && less(a[j], a[j - h]); j -= h) {
                    exch(a, j, j - h);
                }
            }
　　　　　　　h = h / 3; //h = h / 2;

　　　　} 
　　}
 　　private static boolean less(Comparable v, Comparable w) 
　　{ 
　　　　return v.compareTo(w) < 0; 
　　　　//if v < w v.compareTo(w) return -1 , then function return true;  
　　} 

　　private static void exch(Comparable[] a, int i, int j) { 
　　　　Comparable t = a[i]; a[i] = a[j]; a[j] = t; 
　　}
　 public static boolean isSorted(Comparable[] a) { 
　　　　for (int i = 1; i < a.length; i++) { 
　　　　　　if (less(i, i + 1)) 
　　　　　　　　return false; 
　　　　} 
　　　　return true; 
　　} 
}