首先最小生成树有这么两个性质
1.不同的最小生成树中,每种权值的边出现的个数是确定的
2.不同的生成树中,某一种权值的边连接完成后,形成的联通块状态是一样的
打个比方,以下图为例(图是网上的)
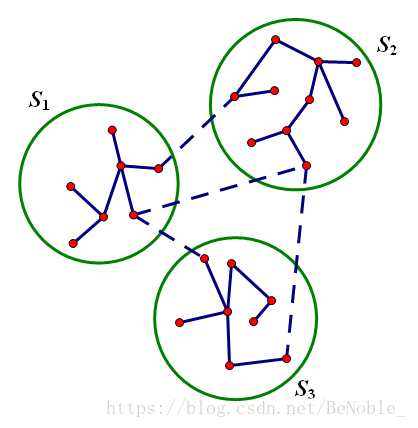
虚线代表边权相同的边。那么我们可以先把连通块内的做完,缩点,变成这样
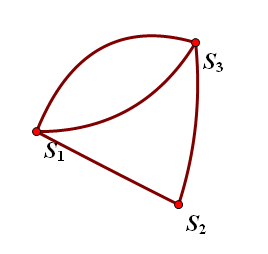
然后我们对这个新的连通块做一次矩阵树
根据乘法原理,最后的答案就是所有的乘起来
//minamoto
#include<bits/stdc++.h>
#define rint register int
using namespace std;
const int N=105,M=1005,P=31011;
#define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
int read(){
int res,f=1;char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
struct eg{
int u,v,w;
inline bool operator <(const eg &b)const{return w<b.w;}
}e[M];
int n,m,ans=1,fa[N],bl[N],vis[N],g[N][N],G[N][N];vector<int>s[N];
inline int find(int x,int *fa){return fa[x]==x?x:fa[x]=find(fa[x],fa);}
inline int add(int x,int y){return x+y>=P?x+y-P:x+y;}
inline int dec(int x,int y){return x-y<0?x-y+P:x-y;}
int det(int n){
int ans=1,f=1;
for(rint i=1;i<=n;++i)for(rint j=1;j<=n;++j)G[i][j]=add(G[i][j],P);
for(rint i=1;i<=n;++i){
for(rint j=i+1;j<=n;++j)while(G[j][i]){
int t=G[i][i]/G[j][i];
for(rint k=i;k<=n;++k)
G[i][k]=dec(G[i][k],t*G[j][k]%P);
for(rint k=i;k<=n;++k)swap(G[i][k],G[j][k]);f=-f;
}
if(!G[i][i])return 0;
ans=ans*G[i][i]%P;
}
return add(f*ans,P);
}
void calc(){
for(rint i=1;i<=n;++i)if(vis[i])s[find(i,fa)].push_back(i),vis[i]=0;
for(rint i=1;i<=n;++i)if(s[i].size()>1){
int t=s[i].size();memset(G,0,sizeof(G));
for(rint j=1;j<=t;++j)for(rint k=j+1;k<=t;++k){
int u=s[i][j-1],v=s[i][k-1];
if(g[u][v]){
G[j][k]=G[k][j]=-g[u][v];
G[j][j]+=g[u][v],G[k][k]+=g[u][v];
}
}
ans=ans*det(t-1)%P;
for(rint j=1;j<=t;++j)bl[s[i][j-1]]=i;
}
for(rint i=1;i<=n;++i)vector<int>().swap(s[i]),fa[i]=bl[i]=find(i,bl);
}
int main(){
// freopen("testdata.in","r",stdin);
n=read(),m=read();for(rint i=1;i<=n;++i)fa[i]=bl[i]=i;
for(rint i=1;i<=m;++i)e[i].u=read(),e[i].v=read(),e[i].w=read();
sort(e+1,e+1+m),e[0].w=e[1].w;
for(rint i=1;i<=m;++i){
if(e[i].w!=e[i-1].w)calc();
int u=find(e[i].u,bl),v=find(e[i].v,bl);
if(u!=v){
vis[u]=vis[v]=1;
++g[u][v],++g[v][u];
fa[find(u,fa)]=find(v,fa);
}
}calc();
for(rint i=2;i<=n;++i)if(bl[i]!=bl[i-1])return puts("0"),0;
printf("%d
",ans);return 0;
}