数据清洗
- 数值缺失
1.略去该组数据
2.数值填充:1)随机数;2)统一的全局常量,如:UNKNOWN;3)均值、中值;4)按类别的中值、均值;5)回归、决策树等得到的预测值;
- 噪声数据的平滑:随机噪声或偏差引起噪声
1.装箱法:按邻值实现

2.拟合回归函数以平滑数据
3.异常数据分析:在聚合后簇外的数据认为异常
数据整合:
1.匹配来自不同数据源的相同数据
2.利用相关性分析判定数据冗余:
- 名词性(标称)特征数据:chi-square相关性
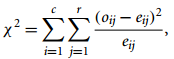
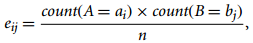
其中,特征A={a1,a2,...,ac}与B={c1,c2,...,cr}各c和r种不同类型的标称值,o_ij为元组(A=a_i,B=b_j)出现的观测频率,e_ij为(A=a_i,B=b_j)出现频率的期望值,n为数据总数目。chi-square要验证的假设是A、B间是不相关的,该假设基于(r-1)*(c-1)自由度下的置信水平,当chi-square数值大于该置信值,则假设不成立,A、B之间相关。
- 数值性特征数据的相关性分析:相关系数
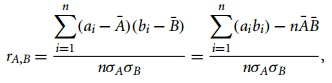
其中,-1<=r_AB<=1,正/负相关。另外,相关性并不意味着因果性,例如某一地区的医院数目和盗窃案数目存在相关性,但是二者并不存在因果,因为它们实际与人口数有因果关系。
- 数值性特征数据的相关性分析:协方差
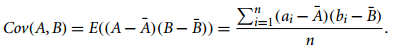
其中,协方差为0时二者不相关。而方差为A=B时协方差的特例。
- 数值冲突:如单位不同
数据精简
1.总揽:
- 目的:减少数据量,同时尽量保证数据携带信息的完整性
- 方法:降维(小波变换、主成分分析)、数值归约、数据压缩
2.降维:小波变换
- 实现:将数据变换为用小波系数表示的向量,由于小波变换后的数据经过截断压缩后仍然可以很好的保留原始数据携带的信息,所以这样变换后的数据具有稀疏性,同时该技术也可以在移除噪声数据的同时而不必平滑掉主要的特征
- 对比DFT:DWT稀疏压缩的效果一般更好、DWT有多种类型
3.降维:主成分分析
- 实现:
- 对比:小波变换更适合处理高维数据,主成分分析更适合处理稀疏数据
4.特征子集选择:
- 分步前向特征选择:每次都向结果中加入当前余下的原始数据中最好的特征到新的数据中
- 分步后向选择 :每次均从数据集中移除当前最差不特征
- 前后向特征选择组合
5.决策树归纳法:利用数据构造的决策树中没有出现在树节点中的属性认为是不相关特征
6.参数化的数据精简:回归与对数线性模型
7.柱状图分桶数据精简:1)等宽策略;2)等频策略
8.聚类
9.采样:1)有放回采样;2)无放回采样;3)按簇采样;4)分层采样;
数据变换及其离散化
1. 平滑:装箱、回归、聚类以移除噪声数据
2.属性构造:生成新的特征
3.属性聚合
4.归一化:(-1,1)、(0,1)
5.离散化
6.标称数据的分层
引用:
[1] Han J, Pei J, Kamber M. Data mining: concepts and techniques[M]. Elsevier, 2011.