深入学习树---二叉树基础

数是数据结构中的重中之重，尤其以各类二叉树为学习的难点。一直以来，对于树的掌握都是模棱两可的状态，现在希望通过写一个关于二叉树的专题系列。在学习与总结的同时，更加深入的了解

掌握二叉树。本系列包含的树包括

1. 一般二叉树
2. 完全二叉树
3. 满二叉树
4. 线索二叉树
5. 霍夫曼树
6. 二叉排序树
7. 平衡二叉树
8. 红黑树
9. B 树

一、重点概念

节点：是数据结构的基础，是构成复杂数据结构的基本组成单位

树： 是 n 个节点的有限集， n=0 时称为空树，在任意一棵非空树中

• 有且仅有一个特定的称为根（Root）节点
• 当 n > 1 时，其余节点可分为 m 个互不相交的有限集 T1 ，T2 ... Tn ，其中每一个集合本身又是一棵树，并且称为根的子树
• 树结构中只有一个节点是根节点
• 子树的个数没有限制，但一定的互不相交的

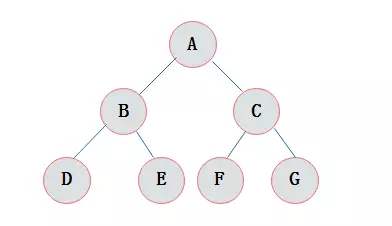
如下是一棵普通的树

 节点的度：节点拥有子树数目称为节点的度 

 树的度：子节点最大的度称为树的度

 节点的关系

节点的子节点称为该节点的孩子节点，响应的该节点称为孩子节点的双亲节点

同一个双亲节点的孩子之间互称为 兄弟节点

节点层次

从根节点开始，根为第一层，根的孩子称为第二层，以此类推

 二、二叉树

二叉树是 n 个节点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根节点或者两棵互不相交的，分别成为根节点的左子树和右子树组成。

 二叉树的特点

1. 每个节点最多有2个子节点，所以二叉树中不存在度大于2的节点
2. 左子树和右子树是由顺序的，次序不能颠倒
3. 即使某个节点只有一棵子树，也要区别是左子树还是右子树

二叉树的性质

1.  在二叉树的第 i 层上做多有 2 ^i-1 个几点
2. 二叉树的深度为 k , 那么做多有 2^k-1 个节点
3. n₀=n₂+1 , n₀ 标识度数为0 ，n₂ 表示度数为2，即 叶子节点 = 双分支节点 +1
4. 在完全二叉树中，具备 n 个节点的完全二叉树的深度为【log₂n】+1 ，【log₂n】向下取整
5. 若对 n 个节点的完全二叉树从上到下，从左到右 进行 1~n 编号，则对完全二叉树任意编号为 i 的节点有如下特征
   1. 若 i=1 ,则该节点为根节点，i!=1,i/2 节点为其双亲节点
   2. 若i*2>n,则该节点无左孩子
   3. 若i*2+1>n ,则该节点无右孩子节点

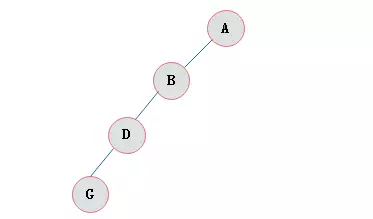
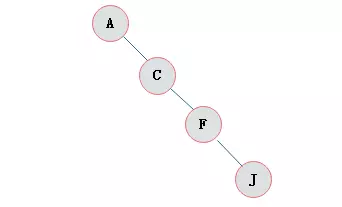
斜树：所以的节点都只有左子树叫做左斜树，所以的节点只有右节点的树叫右斜树，统称为斜树

 

 满二叉树：如果所有的分支节点都存在左子树和右子树，并且所有的叶子都在同一层则称为满二叉树

1.  叶子只能出现在最下一层
2. 非叶子节点的度一定是2
3. 在深度相同的二叉树中，满二叉树节点数最多，叶子最多

   

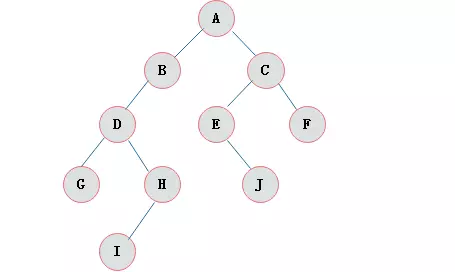
完全二叉树：对一棵具有 n 个节点的二叉树按层编号，如果编号为 i 的节点与同样深度的满二叉树完全相同，节点从左到有依次排列

1. 叶子节点只能出现在最下层与次下层
2. 最下层的叶子节点集中在数的左部
3. 次下层如果有叶子节点，那么一定连续
4. 如果某节点的度为1，则一定只有左子树，没有右子树
5. 满二叉树一定是完全二叉树

三、存储顺序

顺序存储：二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点，并且结点的存储位置，就是数组的下标索引。

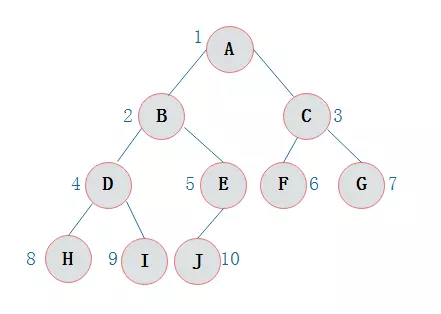
图3.6所示的一棵完全二叉树采用顺序存储方式，如图3.7表示：

 

由图3.7可以看出，当二叉树为完全二叉树时，结点数刚好填满数组。
那么当二叉树不为完全二叉树时，采用顺序存储形式如何呢？例如：对于图3.8描述的二叉树：

 其中浅色结点表示结点不存在。那么图3.8所示的二叉树的顺序存储结构如图3.9所示：

 

 

其中，∧表示数组中此位置没有存储结点。此时可以发现，顺序存储结构中已经出现了空间浪费的情况。
那么对于图3.3所示的右斜树极端情况对应的顺序存储结构如图3.10所示：

由图3.10可以看出，对于这种右斜树极端情况，采用顺序存储的方式是十分浪费空间的。因此，顺序存储一般适用于完全二叉树。

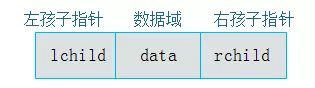
二叉链表

既然顺序存储不能满足二叉树的存储需求，那么考虑采用链式存储。由二叉树定义可知，二叉树的每个结点最多有两个孩子。因此，可以将结点数据结构定义为一个数据和两个指针域。

表示方式如图3.11所示：

typedef struct BiTNode{
    TElemType data;//数据
    struct BiTNode *lchild, *rchild;//左右孩子指针
} BiTNode, *BiTree;

所示的二叉树可以采用下图表示。　

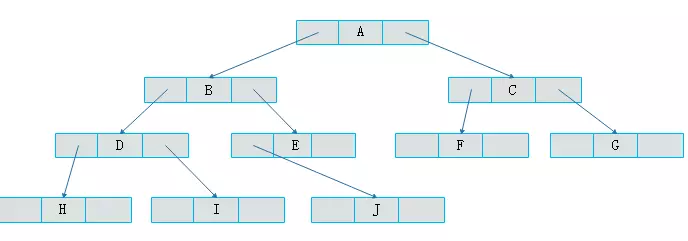
 图中采用一种链表结构存储二叉树，这种链表称为二叉链表

四、遍历

二叉树的遍历是指从二叉树的根节点出发，按照某种次序依次访问二叉树中的所有节点，使得每个节点被访问一次，有四种方式

1. 前序遍历
2. 中序遍历
3. 后序遍历
4. 层次遍历

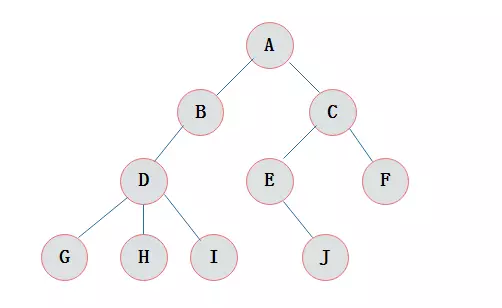
假设存在如下二叉树：

前序遍历：ABDHIEJCFG

中序遍历：HDIBJEAFCG

后续遍历：HIDJEBFGCA

层次遍历：ABCDEFGHIJ

遍历顺序可以按照：头节点在当前数中出现的位置，在头左右即为前序等

• 前序+中序 / 后序+中序 可以推测出二叉树
• 前序 + 后序 不能推测出二叉树

数据结构网址：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

参考：https://www.jianshu.com/u/55255d4c9fd5

参考：https://www.jianshu.com/p/bf73c8d50dc2