题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1506
题意:
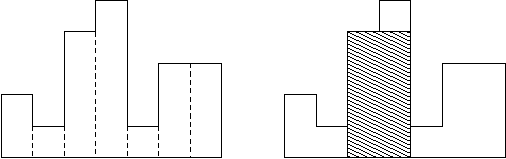
给出n个数(如图代表矩形的高,矩形的宽统一为1)。问合并成的图形中,内置最大矩形面积是多少?
思路:a[i]代表每个矩形的高;以第i个矩形的高为内置矩形的高,l[i]表示该内置矩形的左边,r[i]代表右边。
问题转化为求l[i]和r[i]。
求l[i]和r[i]用类似于链表的方法,详见代码。

1 #include <iostream>
2 using namespace std;
3
4 const int N = 100005;
5
6 int l[N], r[N];
7 long long a[N];
8 long long max2(long long x, long long y)
9 {
10 return x > y ? x : y;
11 }
12
13 int main()
14 {
15 int n;
16 while(cin>>n)
17 {
18 if(n==0) break;
19 for(int i=1; i<=n; i++)
20 {
21 cin >> a[i];
22 l[i] = r[i] = i;
23 }
24 a[0] = a[n+1] = -1;
25 for(int i=1; i<=n; i++)
26 {
27 while(l[i]-1>=1 && a[l[i]-1]>=a[i])
28 l[i] = l[l[i]-1];
29 }
30 for(int i=n; i>=1; i--)
31 {
32 while(r[i]+1<=n && a[r[i]+1]>=a[i])
33 r[i] = r[r[i]+1];
34 }
35 /*
36 cout << " ";
37 for(int i=1; i<=n; i++)
38 cout << l[i] << " ";
39 cout << endl;
40 cout << " ";
41 for(int i=1; i<=n; i++)
42 cout << r[i] << " ";
43 cout << endl;
44 */
45 long long ans = 0;
46 for(int i=1; i<=n; i++)
47 {
48 ans = max2(ans, a[i]*(r[i]-l[i]+1)); //精度问题,a[]要开成long long,否则"a[i]*(r[i]-l[i]+1)"这句是按int计算在类型转换成long long,计算过程溢出
49 }
50 cout << ans << endl;
51 }
52 return 0;
53 }
2 using namespace std;
3
4 const int N = 100005;
5
6 int l[N], r[N];
7 long long a[N];
8 long long max2(long long x, long long y)
9 {
10 return x > y ? x : y;
11 }
12
13 int main()
14 {
15 int n;
16 while(cin>>n)
17 {
18 if(n==0) break;
19 for(int i=1; i<=n; i++)
20 {
21 cin >> a[i];
22 l[i] = r[i] = i;
23 }
24 a[0] = a[n+1] = -1;
25 for(int i=1; i<=n; i++)
26 {
27 while(l[i]-1>=1 && a[l[i]-1]>=a[i])
28 l[i] = l[l[i]-1];
29 }
30 for(int i=n; i>=1; i--)
31 {
32 while(r[i]+1<=n && a[r[i]+1]>=a[i])
33 r[i] = r[r[i]+1];
34 }
35 /*
36 cout << " ";
37 for(int i=1; i<=n; i++)
38 cout << l[i] << " ";
39 cout << endl;
40 cout << " ";
41 for(int i=1; i<=n; i++)
42 cout << r[i] << " ";
43 cout << endl;
44 */
45 long long ans = 0;
46 for(int i=1; i<=n; i++)
47 {
48 ans = max2(ans, a[i]*(r[i]-l[i]+1)); //精度问题,a[]要开成long long,否则"a[i]*(r[i]-l[i]+1)"这句是按int计算在类型转换成long long,计算过程溢出
49 }
50 cout << ans << endl;
51 }
52 return 0;
53 }
