1. 差分脉冲编码调制
如果两个相邻抽样值之间的相关性很大,那么它们的差值就较小,这样,仅对差值量化可以使用较少的比特数,此即差分PCM,或DPCM。
为了理论方便,我们将采样和量化分开,并用不带上三角的$X_n$和带上三角的$hat{X} _n$分别表示采样值和量化值。
最直接的想法,量化器的输入就是$X_n$-$X_{n-1}$。但这会引起积累误差。例如:
$X_0=1.1$,$X_1=2.2$,$X_3=3.3$,$cdots$,$X_9=9.9$,$X_{10}=11.0$
每次量化值均为$hat{Y} _n=1$,累积误差将越来越大。
为了避免累积误差,我们使用下面的式子作为量化器的输入:
$Y_n=X_n-sumlimits_{k=1}^{n} hat{Y} _{n-k}$
将差分转为递归形式,可画出如下框图:
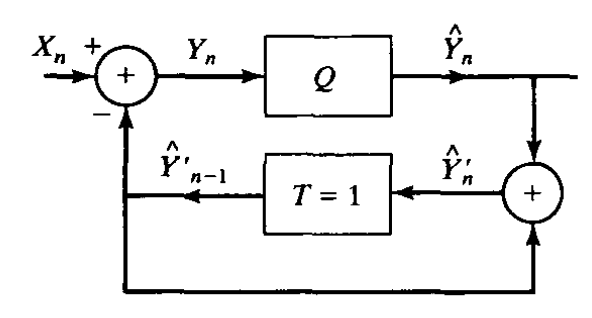
$Y_n=X_n-hat{Y'}_{n-1}$
$hat{Y'}_n=hat{Y}_n+hat{Y'}_{n-1}$
接收端:
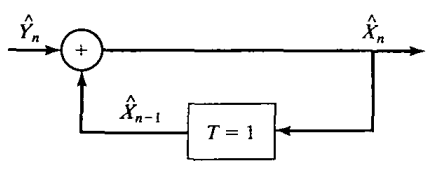
$hat{X}_n=hat{Y}_n + hat{X}_{n-1}$