题目描述
给定一个由 nn 行数字组成的数字梯形如下图所示。
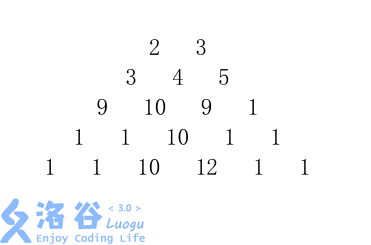
梯形的第一行有 mm 个数字。从梯形的顶部的 mm 个数字开始,在每个数字处可以沿左下或右下方向移动,形成一条从梯形的顶至底的路径。
分别遵守以下规则:
-
从梯形的顶至底的 m 条路径互不相交;
-
从梯形的顶至底的 m 条路径仅在数字结点处相交;
-
从梯形的顶至底的 m 条路径允许在数字结点相交或边相交。
输入输出格式
输入格式:
第 11 行中有 22 个正整数 mm 和 nn,分别表示数字梯形的第一行有 mm 个数字,共有 nn 行。接下来的 nn 行是数字梯形中各行的数字。
第 11 行有 mm 个数字,第 22 行有 m+1m+1 个数字,以此类推。
输出格式:
将按照规则 11,规则 22,和规则 33 计算出的最大数字总和并输出,每行一个最大总和。
输入输出样例
说明
注意细节还是比较好建图的
重新建三次会超时三个点QAQ

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define inf 0x3f3f3f3f #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// const int N=10000001; int n,m,S,T,maxflow,mincost,last[N],pre[N],dis[N],flow[N]; bool vis[N]; struct Edge{ int next,to,flow,dis; }edge[N<<1]; int pos=1,head[N]; void init() { pos=1; CLR(head,0); mincost=maxflow=0; } queue <int> q; void add(int from,int to,int flow,int dis) { edge[++pos].next=head[from]; edge[pos].flow=flow; edge[pos].dis=dis; edge[pos].to=to; head[from]=pos; edge[++pos].next=head[to]; edge[pos].flow=0; edge[pos].dis=-dis; edge[pos].to=from; head[to]=pos; } bool spfa(int s,int t) { CLR(dis,0x3f); CLR(flow,0x3f); CLR(vis,0); while (!q.empty()) q.pop(); dis[s]=0; pre[t]=-1; q.push(s); vis[s]=1; int tot=0; while (!q.empty()) { int now=q.front(); q.pop(); vis[now]=0; for (int i=head[now]; i; i=edge[i].next) { int to=edge[i].to; if (edge[i].flow>0 && dis[to]>dis[now]+edge[i].dis) { dis[to]=edge[i].dis+dis[now]; flow[to]=min(edge[i].flow,flow[now]); last[to]=i; pre[to]=now; if (!vis[to]) { q.push(to); vis[to]=1; } } } } return pre[t]!=-1; } void MCMF(int s,int t) { while (spfa(s,t)) { int now=t; maxflow+=flow[t]; mincost+=flow[t]*dis[t]; while (now!=s) { edge[last[now]].flow-=flow[t]; edge[last[now]^1].flow+=flow[t]; now=pre[now]; } } } int s,t,mp[20][200],id[20][200],cnt=3; int main() { s=0,t=1; RII(n,m); rep(i,1,m) rep(j,1,n+i-1) { RI(mp[i][j]);id[i][j]=++cnt; } int T=cnt; rep(i,1,m) rep(j,1,n+i-1) { add(id[i][j],id[i][j]+T,1,-mp[i][j]); if(i==m)continue; add(id[i][j]+T,id[i+1][j],1,0); add(id[i][j]+T,id[i+1][j+1],1,0); } rep(i,1,n)add(s,id[1][i],1,0); rep(i,1,n+m-1)add(id[m][i]+T,t,1,0); MCMF(s,t); cout<<-mincost<<endl; init(); rep(i,1,m) rep(j,1,n+i-1) { add(id[i][j],id[i][j]+T,n,-mp[i][j]); if(i==m)continue; add(id[i][j]+T,id[i+1][j],1,0); add(id[i][j]+T,id[i+1][j+1],1,0); } rep(i,1,n)add(s,id[1][i],1,0); rep(i,1,n+m-1)add(id[m][i]+T,t,n,0); MCMF(s,t); cout<<-mincost<<endl; init(); rep(i,1,m) rep(j,1,n+i-1) { add(id[i][j],id[i][j]+T,n,-mp[i][j]); if(i==m)continue; add(id[i][j]+T,id[i+1][j],n,0); add(id[i][j]+T,id[i+1][j+1],n,0); } rep(i,1,n)add(s,id[1][i],1,0); rep(i,1,n+m-1)add(id[m][i]+T,t,n,0); MCMF(s,t); cout<<-mincost<<endl; }
调试了一年 原来错误是数组开小了。。 20的范围开成了20.。。
另外一种init的方式 遍历所有边 将正向边的流加上反向边 反向边的流清零 最大流和最小费用清零 就可以啦 这样可以避免一些重新建图的繁琐操作 直接加边即可

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define inf 0x3f3f3f3f #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// const int N=4e3+34; const int M=2e5+52; int n,m,S,T,maxflow,mincost,last[N],pre[N],dis[N],flow[N]; bool vis[N]; struct Edge{ int next,to,flow,dis; }edge[M<<1]; int pos=1,head[M<<1]; void init() { pos=1; CLR(head,0); mincost=maxflow=0; } queue <int> q; void add(int from,int to,int flow,int dis) { edge[++pos].next=head[from]; edge[pos].flow=flow; edge[pos].dis=dis; edge[pos].to=to; head[from]=pos; edge[++pos].next=head[to]; edge[pos].flow=0; edge[pos].dis=-dis; edge[pos].to=from; head[to]=pos; } bool spfa(int s,int t) { CLR(dis,0x3f); CLR(flow,0x3f); CLR(vis,0); while (!q.empty()) q.pop(); dis[s]=0; pre[t]=-1; q.push(s); vis[s]=1; int tot=0; while (!q.empty()) { int now=q.front(); q.pop(); vis[now]=0; for (int i=head[now]; i; i=edge[i].next) { int to=edge[i].to; if (edge[i].flow>0 && dis[to]>dis[now]+edge[i].dis) { dis[to]=edge[i].dis+dis[now]; flow[to]=min(edge[i].flow,flow[now]); last[to]=i; pre[to]=now; if (!vis[to]) { q.push(to); vis[to]=1; } } } } return pre[t]!=-1; } void MCMF(int s,int t) { while (spfa(s,t)) { int now=t; maxflow+=flow[t]; mincost+=flow[t]*dis[t]; while (now!=s) { edge[last[now]].flow-=flow[t]; edge[last[now]^1].flow+=flow[t]; now=pre[now]; } } } int s,t,mp[21][100],id[21][100],cnt=1; int main() { s=0,t=1; RII(n,m); rep(i,1,m) rep(j,1,n+i-1) { RI(mp[i][j]);id[i][j]=++cnt; } int T=cnt; rep(i,1,m) rep(j,1,n+i-1) { add(id[i][j],id[i][j]+T,1,-mp[i][j]); if(i==m)continue; add(id[i][j]+T,id[i+1][j],1,0); add(id[i][j]+T,id[i+1][j+1],1,0); } rep(i,1,n)add(s,id[1][i],1,0); rep(i,1,n+m-1)add(id[m][i]+T,t,1,0); MCMF(s,t); cout<<-mincost<<endl; for(int i=2;i<=pos;i+=2)edge[i].flow+=edge[i^1].flow,edge[i^1].flow=0; maxflow=mincost=0; rep(i,1,m) rep(j,1,n+i-1) { add(id[i][j],id[i][j]+T,inf,-mp[i][j]); } rep(i,1,n+m-1)add(id[m][i]+T,t,inf,0); MCMF(s,t); cout<<-mincost<<endl; for(int i=2;i<=pos;i+=2)edge[i].flow+=edge[i^1].flow,edge[i^1].flow=0; maxflow=mincost=0; rep(i,1,m-1) rep(j,1,n+i-1) { add(id[i][j]+T,id[i+1][j],inf,0); add(id[i][j]+T,id[i+1][j+1],inf,0); } MCMF(s,t); cout<<-mincost<<endl; }
