A. Circle Metro
题意:一个车站共有n个点 首位连成一个环 也就是1和n相邻 一辆车从x1开始向y1顺时针开 一辆车从x2开始逆时针开
问是否有一个时刻 两辆车在同一个车站
签到模拟题:

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f #define lson l,m,pos<<1 #define rson m+1,r,pos<<1|1 const int N=100000; int main() { int n,x1,x2,y1,y2; cin>>n>>x1>>y1>>x2>>y2; if(x1==x2){cout<<"YES";return 0;} while(1) { x1++;if(x1==n+1)x1=1; x2--;if(x2==0)x2=n; if(x1==x2){cout<<"YES";return 0;} if(x2==y2)break; if(x1==y1)break; } cout<<"NO"; return 0; }
B. Pairs (30000 2s)
题意:给出n对数字 试问是否存在两个数x、y 使得任意一对数 这一对数其中至少有一个和x或y相等
比赛的时候一直在想匈牙利算法 不过就算匈牙利能做时间应该也不允许)
直接暴力:当两队数完全不一样的时候 此时如果有解 答案肯定在这四个数之中
120ms

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f #define lson l,m,pos<<1 #define rson m+1,r,pos<<1|1 const int N=300000+5; int num[N][2],n,m,a,b,c,d,x,y; bool ok1(int x,int y) { rep(i,1,m) if(num[i][0]!=x&&num[i][0]!=y&&num[i][1]!=x&&num[i][1]!=y ) return 0; return 1; } int main() { RII(n,m); RII(a,b); num[1][0]=a;num[1][1]=b; if(m==1||m==2){cout<<"YES";return 0;} int ok=1; rep(i,2,m) { RII(x,y); num[i][0]=x;num[i][1]=y; if(a!=x&&a!=y&&b!=x&&b!=y) { ok=0;c=x;d=y; } } if(ok){cout<<"YES";return 0;} if(ok1(a,c)||ok1(a,d)||ok1(b,c)||ok1(b,d)){cout<<"YES";return 0;} cout<<"NO"; return 0; }
还有一种更加巧妙而且好打的方法(智商又一次被碾压了)
显然 x y 肯定有一个出自 第一对的 第一个数字或者第二个数字
先假设有x 遍历的时候忽略有x的数对 然后看剩下的数对是否有一个共同值(用一个计数数组记录即可)
然后对y再进行一次

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f #define lson l,m,pos<<1 #define rson m+1,r,pos<<1|1 const int N=300000+5; int n,m,cnt,num[N]; struct numm { int x,y; }s[N]; int main() { RII(n,m); RII(s[1].x,s[1].y); rep(i,2,m) { RII(s[i].x,s[i].y); if(s[i].x==s[1].x||s[i].y==s[1].x)continue; cnt++; num[s[i].x]++,num[s[i].y]++; } bool ok=0; rep(i,1,n)if(num[i]==cnt){ok=1;break;} CLR(num,0); if(ok){cout<<"YES";return 0;} cnt=0; rep(i,2,m) { if(s[i].x==s[1].y||s[i].y==s[1].y)continue; cnt++; num[s[i].x]++;num[s[i].y]++; } rep(i,1,n)if(num[i]==cnt){ok=1;break;} if(ok)puts("YES"); else puts("NO"); return 0; }
跑出来速度居然差不多。。。
C. Increasing by Modulo**
题意:给定一个长度为n的序列 和一个模数m 有一种操作: 选择1-n 任意几个位置 让该位置的数+1 (要%m)
问做少几次操作使得该序列成为不下降序列
各种模拟+贪心 过不了QAQ
这种情况下可以二分答案 在确定答案的情况下贪心策略就十分明显了

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f #define lson l,m,pos<<1 #define rson m+1,r,pos<<1|1 const int N=300000+5; int a[N],n,m,L,R,ans,mid; bool check(int cnt) { int last=0; rep(i,1,n) { if(a[i]==last)continue; int temp=a[i]+cnt;temp%=m; if(temp>a[i]) { if(last<a[i]){last=a[i];} else if(last>temp){return 0;} } else if(temp<a[i]&&last<a[i]&&last>temp) last=a[i]; else if(temp==a[i]) { if(last>a[i])return 0; else last=a[i]; } } return 1; } int main() { RII(n,m); rep(i,1,n)RI(a[i]); L=0,R=m; while(L<=R) { int mid=(L+R)>>1; if(check(mid))ans=mid,R=mid-1; else L=mid+1; } cout<<ans; return 0; }
check函数写的太挫了
仔细想一下一共有6中状态
其中一种直接 结束
两种改last

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f #define lson l,m,pos<<1 #define rson m+1,r,pos<<1|1 const int N=300000+5; int a[N],n,m,L,R,ans,mid; bool check(int cnt) { int last=0; rep(i,1,n) { if(last>a[i]+cnt)return 0; else if(a[i]>last&&(a[i]+cnt)<m||a[i]>last&&(a[i]+cnt)%m<last)last=a[i]; } return 1; } int main() { RII(n,m); rep(i,1,n)RI(a[i]); L=0,R=m; while(L<=R) { int mid=(L+R)>>1; if(check(mid))ans=mid,R=mid-1; else L=mid+1; } cout<<ans; return 0; }
D. Good Triple**
题意:英文比较好懂就不解释了 主要就是求满足条件的 对的数量
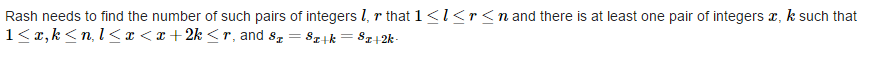
可以枚举左指针 累加每个左指针的对数 这样就不会遗漏了
贪心找到最短的满足条件的右指针(贪心) 然后其右边的(包含该)都能和该左指针组成一个答案

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f #define lson l,m,pos<<1 #define rson m+1,r,pos<<1|1 const int N=300000+5; string s; int n,last; ll ans; int main() { cin>>s; n=s.size(); last=n; repp(i,n-1,0) { for(int k=1;i+2*k<n;k++)//其实可以右界可以改成last更快 下面的代码也可以简化 { if(s[i]==s[i+k]&&s[i+k]==s[i+2*k])//找到第一个就退出 { int temp=i+2*k; if(temp<=last){last=temp;break;} if(temp>last){break;} } } ans+=n-last;//其实是n-1 - last +1 } cout<<ans; return 0; }
