题目描述
小a住的国家被僵尸侵略了!小a打算逃离到该国唯一的国际空港逃出这个国家。
该国有N个城市,城市之间有道路相连。一共有M条双向道路。保证没有自环和重边。
K个城市已经被僵尸控制了,如果贸然闯入就会被感染TAT...所以不能进入。由其中任意城市经过不超过S条道路就可以到达的别的城市,就是危险城市。换句话说只要某个没有被占城市到某个被占城市不超过s距离,就是危险。
小a住在1号城市,国际空港在N号城市,这两座城市没有被侵略。小a走每一段道路(从一个城市直接到达另外一个城市)得花一整个白天,所以晚上要住旅店。安全的的城市旅馆比较便宜要P元,而被危险的城市,旅馆要进行安保措施,所以会变贵,为Q元。所有危险的城市的住宿价格一样,安全的城市也是。在1号城市和N城市,不需要住店。
小a比较抠门,所以他希望知道从1号城市到N号城市所需要的最小花费。
输入数据保证存在路径,可以成功逃离。输入数据保证他可以逃离成功。
输入输出格式
输入格式:
第一行4个整数(N,M,K,S)
第二行2个整数(P,Q)
接下来K行,ci,表示僵尸侵占的城市
接下来M行,ai,bi,表示一条无向边
输出格式:
一个整数表示最低花费
输入输出样例
输入样例#1: 复制
13 21 1 1 1000 6000 7 1 2 3 7 2 4 5 8 8 9 2 5 3 4 4 7 9 10 10 11 5 9 7 12 3 6 4 5 1 3 11 12 6 7 8 11 6 13 7 8 12 13
输出样例#1: 复制
11000
说明
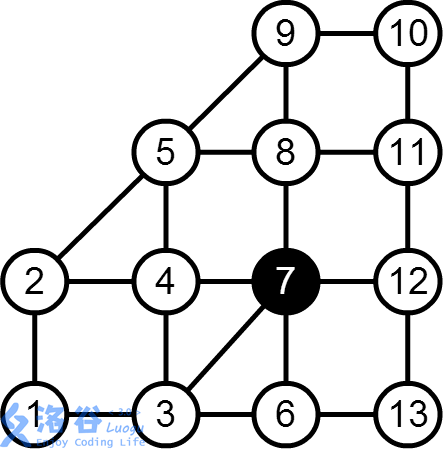
对于20%数据,N<=50
对于100%数据,2 ≦ N ≦ 100000, 1 ≦ M ≦ 200000, 0 ≦ K ≦ N - 2, 0 ≦ S ≦ 100000
1 ≦ P < Q ≦ 100000
先用bfs求出危险的点
然后其实就是裸的最短路 只不过是点权最短路
点权最短路的求法:边权看作其两个端点权之和 结果div2即可
注意染色会被覆盖!

#include<bits/stdc++.h> using namespace std; //input by bxd #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define repp(i,a,b) for(int i=(a);i>=(b);--i) #define RI(n) scanf("%d",&(n)) #define RII(n,m) scanf("%d%d",&n,&m) #define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k) #define RS(s) scanf("%s",s); #define ll long long #define pb push_back #define REP(i,N) for(int i=0;i<(N);i++) #define CLR(A,v) memset(A,v,sizeof A) ////////////////////////////////// #define inf 0x3f3f3f3f3f3f const int N=1e6; const int M=4e7+54; int n,m,k,s,Q,P,x; ll mp[N],dis[N]; int vis[N],unsafe[N]; int head[M],pos; struct Edge { int nex,to; }edge[M]; void add(int a,int b) { edge[++pos].nex=head[a]; head[a]=pos; edge[pos].to=b; } struct Node { ll d,id; bool operator<(Node b)const { return d>b.d; } }; struct bf { int x,d; }; void bfs(int x) { queue<bf>q; CLR(vis,0); vis[x]=1; q.push(bf{x,0}); while(!q.empty()) { bf u=q.front();q.pop(); if(u.d>s)continue; if(u.d==0)mp[u.x]=inf; else mp[u.x]=Q; for(int i=head[u.x];i;i=edge[i].nex) { int v=edge[i].to; if(vis[v])continue; vis[v]=1; q.push(bf{v,u.d+1}); } } } void dijkstra(int s) { rep(i,1,n) dis[i]=inf; dis[s]=0; CLR(vis,0); priority_queue<Node>q; q.push(Node{0,s}); while(!q.empty()) { Node u=q.top();q.pop(); if(vis[u.id])continue; vis[u.id]=1; for(int i = head[u.id];i;i=edge[i].nex) { int v=edge[i].to; if(dis[v]>u.d+mp[u.id]+mp[v]) { dis[v]=u.d+mp[u.id]+mp[v]; q.push(Node{dis[v],v}); } } } } int main() { RII(n,m);RII(k,s); RII(P,Q); rep(i,1,k){RI(x);unsafe[x]=1;} rep(i,1,n)mp[i]=P; while(m--){ int a,b;RII(a,b);add(a,b);add(b,a);} rep(i,1,n) if(unsafe[i]) bfs(i); rep(i,1,n)if(unsafe[i])mp[i]=inf; mp[1]=0; mp[n]=0; dijkstra(1); cout<<dis[n]/2; return 0; }
