P2827 蚯蚓
题目描述
本题中,我们将用符号 (lfloor c floor) 表示对 (c) 向下取整,例如:(lfloor 3.0 floor = lfloor 3.1 floor = lfloor 3.9 floor = 3)。
蛐蛐国最近蚯蚓成灾了!隔壁跳蚤国的跳蚤也拿蚯蚓们没办法,蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。
蛐蛐国里现在共有 (n) 只蚯蚓((n) 为正整数)。每只蚯蚓拥有长度,我们设第 (i) 只蚯蚓的长度为 (a_i)((i=1,2,dots,n)),并保证所有的长度都是非负整数(即:可能存在长度为 (0) 的蚯蚓)。
每一秒,神刀手会在所有的蚯蚓中,准确地找到最长的那一只(如有多个则任选一个)将其切成两半。神刀手切开蚯蚓的位置由常数 (p)(是满足 (0 < p < 1) 的有理数)决定,设这只蚯蚓长度为 (x),神刀手会将其切成两只长度分别为 (lfloor px floor) 和 (x - lfloor px floor) 的蚯蚓。特殊地,如果这两个数的其中一个等于 (0),则这个长度为 (0) 的蚯蚓也会被保留。此外,除了刚刚产生的两只新蚯蚓,其余蚯蚓的长度都会增加 (q)(是一个非负整常数)。
蛐蛐国王知道这样不是长久之计,因为蚯蚓不仅会越来越多,还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物,但是救兵还需要 (m) 秒才能到来……((m) 为非负整数)
蛐蛐国王希望知道这 (m) 秒内的战况。具体来说,他希望知道:
(m) 秒内,每一秒被切断的蚯蚓被切断前的长度(有 (m) 个数);
(m) 秒后,所有蚯蚓的长度(有 (n + m) 个数)。
蛐蛐国王当然知道怎么做啦!但是他想考考你……
输入输出格式
输入格式:
第一行包含六个整数 (n,m,q,u,v,t),其中:(n,m,q) 的意义见【问题描述】;(u,v,t) 均为正整数;你需要自己计算 (p=u / v)(保证 (0 < u < v));(t) 是输出参数,其含义将会在【输出格式】中解释。
第二行包含 nn 个非负整数,为 (a_1, a_2, dots, a_n),即初始时 (n) 只蚯蚓的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。
保证 (1 leq n leq 10^5),(0 leq m leq 7 imes 10^6),(0 < u < v leq 10^9),(0 leq q leq 200),(1 leq t leq 71),(0 leq a_i leq 10^8)。
输出格式:
第一行输出 (left lfloor frac{m}{t} ight floor)个整数,按时间顺序,依次输出第 (t) 秒,第 (2t) 秒,第 (3t) 秒,……被切断蚯蚓(在被切断前)的长度。
第二行输出 (left lfloor frac{n+m}{t} ight floor)个整数,输出 (m) 秒后蚯蚓的长度;需要按从大到小的顺序,依次输出排名第 (t),第 (2t),第 (3t),……的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。即使某一行没有任何数需要输出,你也应输出一个空行。
请阅读样例来更好地理解这个格式。
说明:
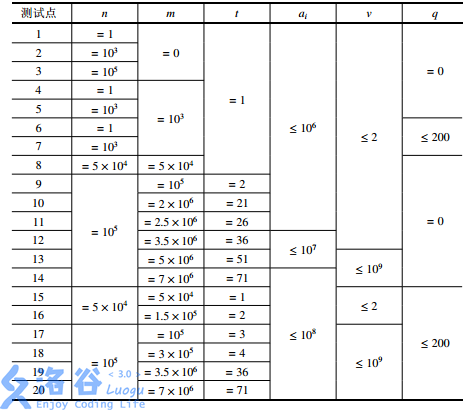
堆的做法很显然,大概有65~80pts,算是送了很多分了
一看输出都强行怕你T,那一定是(O(n))了
记得合并果子有一个双队列(O(n))做法吗?
事实上跟这个题差不多哒
我们开三个队列,一个存放原来的蚯蚓,一个存放被这样切(lfloor px floor)的蚯蚓,另一个存放被(x - lfloor px floorx)这样切的
注意到在后两个队列中先拿出来的一定比后拿出来的要长,具有单调性
对于第一个队列我们可以先排序,然后每次取三个队列中队尾最大的,切开放到相应的队头
增加的量我们可以维护一个被切断的时间点
注意中间过程可能会爆int
Code:
#include <cstdio>
#include <algorithm>
#define ll long long
const int N=8e6;
ll q1[N][2],q2[N][2],q3[N][2],l1=1,l2=1,l3=1,r1,r2,r3;
ll n,m,q,u,v,t,a[N];//n个m刀增q p=u/v t输出
int main()
{
scanf("%lld%lld%lld%lld%lld%lld",&n,&m,&q,&u,&v,&t);
for(int i=1;i<=n;++i)
scanf("%lld",a+i);
r1=n;
std::sort(a+1,a+1+n);
for(int i=1;i<=n;i++) q1[n+1-i][0]=a[i];
for(register ll mx,id,i=1;i<=m;++i)
{
mx=0;
if(l1<=r1&&mx<q1[l1][0]+(i-q1[l1][1]-1)*q) mx=q1[l1][0]+(i-q1[l1][1]-1)*q,id=1;
if(l2<=r2&&mx<q2[l2][0]+(i-q2[l2][1]-1)*q) mx=q2[l2][0]+(i-q2[l2][1]-1)*q,id=2;
if(l3<=r3&&mx<q3[l3][0]+(i-q3[l3][1]-1)*q) mx=q3[l3][0]+(i-q3[l3][1]-1)*q,id=3;
if(i%t==0) printf("%lld ",mx);
if(id==1) ++l1;if(id==2) ++l2;if(id==3) ++l3;
q2[++r2][0]=mx*u/v,q2[r2][1]=i;
q3[++r3][0]=mx-mx*u/v,q3[r3][1]=i;
}
printf("
");ll i=0;
while(l1<=r1||l2<=r2||l3<=r3)
{
ll id,mx=0;++i;
if(l1<=r1&&mx<q1[l1][0]+(m-q1[l1][1])*q) mx=q1[l1][0]+(m-q1[l1][1])*q,id=1;
if(l2<=r2&&mx<q2[l2][0]+(m-q2[l2][1])*q) mx=q2[l2][0]+(m-q2[l2][1])*q,id=2;
if(l3<=r3&&mx<q3[l3][0]+(m-q3[l3][1])*q) mx=q3[l3][0]+(m-q3[l3][1])*q,id=3;
if(i%t==0) printf("%lld ",mx);
if(id==1) ++l1;if(id==2) ++l2;if(id==3) ++l3;
}
printf("
");
return 0;
}
2018.9.1