给定一个树,树上的边都具有权值。
树中一条路径的异或长度被定义为路径上所有边的权值的异或和:
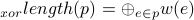
⊕ 为异或符号。
给定上述的具有n个节点的树,你能找到异或长度最大的路径吗?
输入格式
第一行包含整数n,表示树的节点数目。
接下来n-1行,每行包括三个整数u,v,w,表示节点u和节点v之间有一条边权重为w。
输出格式
输出一个整数,表示异或长度最大的路径的最大异或和。
数据范围
1≤n≤1000001≤n≤100000,
0≤u,v<n0≤u,v<n,
0≤w<2310≤w<231
输入样例:
4
0 1 3
1 2 4
1 3 6
输出样例:
7
样例解释
样例中最长异或值路径应为0->1->2,值为7 (=3 ⊕ 4)
算法:dfs + 01字典树
题解:设 D[x] 表示根节点到 x 的路径上所有边权的 xor 值 , 显然有:
D[x] = D[father(x) ] xor weight(x,father(x))
根据上式,我们可以使用dfs,从根节点开始遍历,依次记录每条路径。
又相同的两个数的异或和为0,那么,只要把所求的D[x] 数组像求最大异或对一样就行(最大异或对:https://www.cnblogs.com/buhuiflydepig/p/11306057.html)。
你需要知道它是一棵树。
例如:0 -> 1 -> 2 -> 5 的结果是 4,存再D[5]中。
0 -> 1 的结果是1,存在D[1]中。
现在我们需要求1 -> 5 的结果,就只要把D[1] ^ D[5]就行了,相同的地方异或为0,根据这条性质,就可以得出结果。
#include <iostream> #include <cstdio> #include <vector> using namespace std; const int maxn = 1e5+7; vector<pair<int, int> > g[maxn]; int tree[maxn * 32][2]; int d[maxn]; int tot; void dfs(int u, int fa) { int len = g[u].size(); for(int i = 0; i < len; i++) { pair<int, int> v = g[u][i]; if(v.first != fa) { d[v.first] = d[u] ^ v.second; dfs(v.first, u); } } } void insert(int x) { int root = 0; for(int i = 30; i >= 0; i--) { int idx = (x >> i) & 1; if(tree[root][idx] == 0) { tree[root][idx] = ++tot; } root = tree[root][idx]; } } int search(int x) { int root = 0; int res = 0; for(int i = 30; i >= 0; i--) { int idx = (x >> i) & 1; if(tree[root][1 ^ idx] != 0) { root = tree[root][1 ^ idx]; res |= (1 << i); } else { root = tree[root][idx]; } } return res; } int main() { int n; scanf("%d", &n); for(int i = 0; i < n - 1; i++) { int u, v, w; scanf("%d %d %d", &u, &v, &w); g[u].push_back(make_pair(v, w)); g[v].push_back(make_pair(u, w)); } dfs(0, -1); int ans = 0; for(int i = 0; i < n; i++) { insert(d[i]); ans = max(ans, search(d[i])); } cout << ans << endl; return 0; }