"I've been here once," Mino exclaims with delight, "it's breathtakingly amazing."
"What is it like?"
"Look, Kanno, you've got your paintbrush, and I've got my words. Have a try, shall we?"
There are four kinds of flowers in the wood, Amaranths, Begonias, Centaureas and Dianthuses.
The wood can be represented by a rectangular grid of nn rows and mm columns. In each cell of the grid, there is exactly one type of flowers.
According to Mino, the numbers of connected components formed by each kind of flowers are aa, bb, cc and dd respectively. Two cells are considered in the same connected component if and only if a path exists between them that moves between cells sharing common edges and passes only through cells containing the same flowers.
You are to help Kanno depict such a grid of flowers, with nn and mm arbitrarily chosen under the constraints given below. It can be shown that at least one solution exists under the constraints of this problem.
Note that you can choose arbitrary nn and mm under the constraints below, they are not given in the input.
The first and only line of input contains four space-separated integers aa, bb, cc and dd (1≤a,b,c,d≤1001≤a,b,c,d≤100) — the required number of connected components of Amaranths, Begonias, Centaureas and Dianthuses, respectively.
In the first line, output two space-separated integers nn and mm (1≤n,m≤501≤n,m≤50) — the number of rows and the number of columns in the grid respectively.
Then output nn lines each consisting of mm consecutive English letters, representing one row of the grid. Each letter should be among 'A', 'B', 'C' and 'D', representing Amaranths, Begonias, Centaureas and Dianthuses, respectively.
In case there are multiple solutions, print any. You can output each letter in either case (upper or lower).
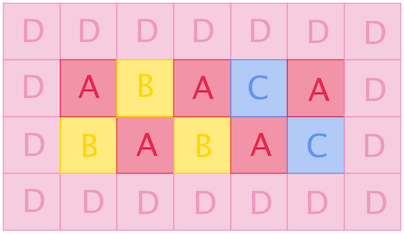
5 3 2 1
4 7
DDDDDDD
DABACAD
DBABACD
DDDDDDD
50 50 1 1
4 50
CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
ABABABABABABABABABABABABABABABABABABABABABABABABAB
BABABABABABABABABABABABABABABABABABABABABABABABABA
DDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDDD
1 6 4 5
7 7
DDDDDDD
DDDBDBD
DDCDCDD
DBDADBD
DDCDCDD
DBDBDDD
DDDDDDD
In the first example, each cell of Amaranths, Begonias and Centaureas forms a connected component, while all the Dianthuses form one.
题意: 告诉你a,b,c,d的个数,要你输出包含这么多个a,b,c,d个数的图
规则:与相同块相联通的是同一个
题解:先构造一个只含有A、B的图,然后i+=2,间隔着往里面加B、C、A、D
QAQ 还是不太会构造题,hzwer了解一下?
QAQorz天下第一


#include<bits/stdc++.h> using namespace std; const int M = 48; const int maxn=64; char mp[maxn][maxn]; int a,b,c,d; int main(){ ios::sync_with_stdio(false); while(cin>>a>>b>>c>>d){ for(int i=0;i<M/2;i++){ for(int j=0;j<M;j++){ mp[i][j]='A'; } } for(int i=M/2;i<M;i++){ for(int j=0;j<M;j++){ mp[i][j]='B'; } } a--,b--; for(int i=0;i<M/2;i+=2){ for(int j=0;j<M;j+=2){ if(b) mp[i][j]='B',b--; else if(c) mp[i][j]='C',c--; } } for(int i=M/2+1;i<M;i+=2){ for(int j=0;j<M;j+=2){ if(a) mp[i][j]='A',a--; else if(d) mp[i][j]='D',d--; } } printf("48 48 "); for(int i=0;i<M;i++){ printf("%s ",mp[i]); } } return 0; }