codeforces 572（Div2）A、B、C、D1、D2、E

Cdoeforces 572（Div2）A、B、C、D1、D2、E

传送门：https://codeforces.com/contest/1189

A.题意：

给你一串长为n的字符串，要求你将其切割为若干个good 的子串，一个子串如果其中0和1的个数不相等，那么这个子串是good子串，输出最少切割后的子串个数和切割后的结果

题解：

最多只用切1次，因为一个串中0和1的个数只有相等和不相等两种情况，如果串中0和1的个数不相等那么就不用切割，否则随便拿头或者拿尾即可

代码：

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
 
typedef long long LL;
typedef long long ll;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********
")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]
"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]
"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]
"
 
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const LL INFLL = 0x3f3f3f3f3f3f3f3f;
struct EDGE {
    int v, nxt;
} edge[maxn << 1];
int head[maxn], tot;
void add_edge(int u, int v) {
    edge[tot].v = v, edge[tot].nxt = head[u], head[u] = tot++;
}
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    int n;
    string str;
    cin >> n >> str;
    int cnt1 = 0, cnt0 = 0;
    for(int i = 0; i < n; i++) {
        if(str[i] == '0') {
            cnt0++;
        } else {
            cnt1++;
        }
    }
    if(cnt1 != cnt0) {
        cout << 1 << endl;
        cout << str << endl;
    } else {
        cout << 2 << endl;
        cout << str.substr(0, n - 1) << " ";
        cout << str.substr(n - 1, 1) << endl;
    }
    return 0;
}

B题意：

给你n个数，要求你将其排成一个数环，要求第i个数小于第i-1、第i+1个数之和，构造出来

题解：

排序后，形成一个环，我们贪心的构造一下，我们取max，sec,th三个最大的数，构成一个环，那么max是放在sec和th之间时，他们三个如果符合条件，那么形成的环里面，按排序顺序输出的时候，i-1项都为三项中的最大项，即一定满足条件

代码：

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
typedef long long ll;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********
")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]
"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]
"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]
"

const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const LL INFLL = 0x3f3f3f3f3f3f3f3f;
struct EDGE {
    int v, nxt;
} edge[maxn << 1];
int head[maxn], tot;
void add_edge(int u, int v) {
    edge[tot].v = v, edge[tot].nxt = head[u], head[u] = tot++;
}
int a[maxn];
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    sort(a + 1, a + n + 1);
    if(a[n - 1] + a[n - 2] <= a[n]) {
        printf("NO
");
    } else {
        printf("YES
");
        printf("%d %d %d ", a[n - 2], a[n], a[n - 1]);
        for(int i = n - 3; i >= 1; i--) {
            printf("%d%c", a[i], i == 1 ? '
' : ' ');
        }

    }
    return 0;
}

C题意：

现在有n个数字，n满足2的幂次，现在要你将每两项结合起来，形成新数列，再将新数列的每两项结合起来，形成一个新数列，依次递推，最后只剩下一项时停止，当结合时，然后两项之和大于10就模10，并且得到一个贡献，现在有m次询问，询问数列[l,r]区间的贡献是多少

题解：

因为是和超过10就有一个贡献，所以区间和有多少个10那么就有多少贡献。。。。

emmm思维题

代码：

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
 
typedef long long LL;
typedef long long ll;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********
")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]
"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]
"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]
"
 
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const LL INFLL = 0x3f3f3f3f3f3f3f3f;
struct EDGE {
    int v, nxt;
} edge[maxn << 1];
int head[maxn], tot;
void add_edge(int u, int v) {
    edge[tot].v = v, edge[tot].nxt = head[u], head[u] = tot++;
}
int n;
int a[maxn];
int sum[maxn];
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        sum[i] = sum[i - 1] + a[i];
    }
 
    int m;
    scanf("%d", &m);
    while(m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d
", (sum[r] - sum[l - 1]) / 10);
    }
}

D1题意：

给你一颗树，边权任意，你每次可以选择任意两个叶子节点在路径上add一个任意的实数边权，问你是否可以形成边权的任意组合

题解：

拿这个图来举例

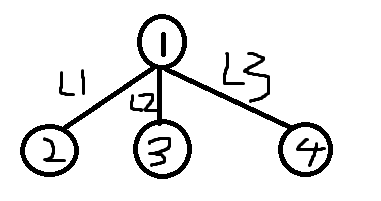
我要想得到（L1，L2，L3）（x，0，0）这种组合，那么我只需要在2，3的路径上添加x/2，2，4的路径上添加上x/2，3，4的路径上添加上-x/2，就可以得到这种组合了。

即如果图中有度数为1的点若干个，度大于等于3的点若干个，我就可以组合出任意组合来

即，如果我的点的度数为2，就会导致false

所以判断一下度数就好了

代码：

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
 
typedef long long LL;
typedef long long ll;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********
")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]
"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]
"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]
"
 
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const LL INFLL = 0x3f3f3f3f3f3f3f3f;
struct EDGE {
    int v, nxt;
} edge[maxn << 1];
int head[maxn], tot;
void add_edge(int u, int v) {
    edge[tot].v = v, edge[tot].nxt = head[u], head[u] = tot++;
}
int degree[maxn];
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    memset(head, -1, sizeof(head));
    tot = 0;
    int n;
    scanf("%d", &n);
    for(int i = 1, u, v; i < n; i++) {
        scanf("%d%d", &u, &v);
        degree[u]++;
        degree[v]++;
    }
    bool flag = true;
    for(int i = 1; i <= n; i++) {
        if(degree[i] == 2) {
            flag = false;
        }
    }
    if(flag) {
        printf("YES
");
    } else {
        printf("NO
");
    }
 
    return 0;
}

D2题意：

和D1题意差不多

给你一颗树，但是现在给你了要求的边权，问你怎么样构造才能构造出这样的边权

题解：

要求的路径上有四种情况

1.两个端点u，v都是叶子节点

2.u在叶子节点，v不在

3.v在叶子节点，u不在

4.u，v都不在叶子结点

2和3情况一样

那么我们可以这样来讨论

对于第一种情况，改变u，v这两点上的路径边权即可

对于第二、三种情况，我们可以找出，一个非叶子节点v的两个叶子节点（因为是一颗完全二叉树，一定可以向下找出两个叶子节点，这个可以dfs一下实现），假设找到的两个叶子节点是点a和点b，那么我们可以u->a加上val/2

u->b加上val/2，最后a->b减去val/2即可

对于第四种情况同理，我们可以找到u的两个叶子节点a，b，v的两个叶子节点c，d，然后和刚才的方法一样，

a ->c加上val / 2，然后b -> d去加上val / 2，最后，a ->b减去val / 2，以及c -> d去减去val / 2即可。

代码：

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long LL;
typedef long long ll;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********
")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]
"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]
"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]
"

const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const LL INFLL = 0x3f3f3f3f3f3f3f3f;
struct EDGE {
    int v, w, nxt;
} edge[maxn << 1];
int head[maxn], tot;
void add_edge(int u, int v, int w) {
    edge[tot].v = v, edge[tot].w = w; edge[tot].nxt = head[u], head[u] = tot++;
}
int degree[maxn];
// strcut Path{
//     int u, v, w;
//     P() {};
//     P(int _u, int _v, int _w) {
//         u = _u, v = _v, w = _w;
//     }
// } path[maxn];
pair<pair<int, int>, int> path[maxn];

inline int dfs(int u, int fa) {
    if(degree[u] == 1) return u;
    else {
        for(int i = head[u], v; ~i; i = edge[i].nxt) {
            v = edge[i].v;
            if(v == fa) continue;
            else return dfs(v, u);
        }
    }
    return u;
}

vector<pair<pair<int, int>, int>> ans;
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    memset(head, -1, sizeof(head));
    tot = 0;
    int n;
    scanf("%d", &n);
    for(int i = 1, u, v, w; i < n; i++) {
        scanf("%d%d%d", &u, &v,&w);
        add_edge(u, v, w);
        add_edge(v, u, w);
        degree[u]++;
        degree[v]++;
        path[i] = make_pair(make_pair(u, v), w);
    }
    for(int i = 1; i <= n; i++) {
        if(degree[i] == 2) {
            printf("NO
");
            return 0;
        }
    }
    printf("YES
");
    for(int i = 1, u, v; i < n; i++) {
        tie (u, v) = path[i].first;  //u、v就是path[i]的u、v
        pair<int, int> UU = {-1, -1};
        for(int j = head[u], tv; ~j; j = edge[j].nxt) {
            tv = edge[j].v;
            if(tv == v) continue;
            int tmp = dfs(tv, u);
            if(UU.first == -1) UU.first = tmp;
            else if(UU.second == -1) {
                UU.second = tmp;
                break;
            }
        }
        pair<int, int> VV = {-1, -1};
        for(int j = head[v], tu; ~j; j = edge[j].nxt) {
            tu = edge[j].v;
            if(tu == u) continue;
            int tmp = dfs(tu, v);
            if(VV.first == -1) VV.first = tmp;
            else if(VV.second == -1) {
                VV.second = tmp;
                break;
            }
        }
        if(degree[u] == 1) UU = {u, u};
        if(degree[v] == 1) VV = {v, v};
        int real = path[i].second / 2;
        ans.push_back(make_pair(make_pair(UU.first, VV.first), real));
        ans.push_back(make_pair(make_pair(UU.second, VV.second), real));
        if(UU.first != UU.second) ans.push_back(make_pair(make_pair(UU.first, UU.second), -real));
        if(VV.first != VV.second) ans.push_back(make_pair(make_pair(VV.first, VV.second), -real));
    }
    printf("%d
", (int)ans.size());
    for(int i = 0; i < ans.size(); i++) printf("%d %d %d
", ans[i].first.first, ans[i].first.second, ans[i].second);
    return 0;
}

E题意：

给你n,p,k，要你求有多少对数，满足

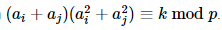
题解：

公式推导如下：

[(a_i+a_j)(a_i^2+a_j^2)=kmodp\ (a_i^2-a_j^2)(a_i^2+a_j^2)\%p=k(a_i-a_j)\%p\ (a_i^4-ka_i)\%p=(a_j^4-ka_j)\%p ]

所以得到(a_i^4-ka_i\%p)的个数，组合一下即可

代码：

#include <set>
#include <map>
#include <deque>
#include <queue>
#include <stack>
#include <cmath>
#include <ctime>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
 
typedef long long LL;
typedef long long ll;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pLi;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********
")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]
"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]
"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]
"
 
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const LL INFLL = 0x3f3f3f3f3f3f3f3f;
struct EDGE {
    int v, nxt;
} edge[maxn << 1];
int head[maxn], tot;
void add_edge(int u, int v) {
    edge[tot].v = v, edge[tot].nxt = head[u], head[u] = tot++;
}
map<int, int> mp;
LL a[maxn];
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    int n, k, p;
    scanf("%d%d%d", &n, &p, &k);
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
        LL t = ((a[i] * a[i] % p * a[i] % p * a[i] % p) % p + p - (k * a[i]) % p + p) % p;
        mp[t]++;
    }
    LL ans = 0;
    map<int, int>::iterator it;
    for(it = mp.begin(); it != mp.end(); it++) {
        int val = it->first;
        int sz = it->second;
        // debug2(val, sz);
        ans += sz * (sz - 1) / 2;
    }
    printf("%lld
", ans);
 
    return 0;
}