CCPC-Winter Camp div2 day8 A

---恢复内容开始---

题目：

题解：

我们考虑第i个叶子节点的情况，根据题目给的输入条件，我们可以知道，深度大的节点的序号一定是大于深度浅的节点的序号的

如图

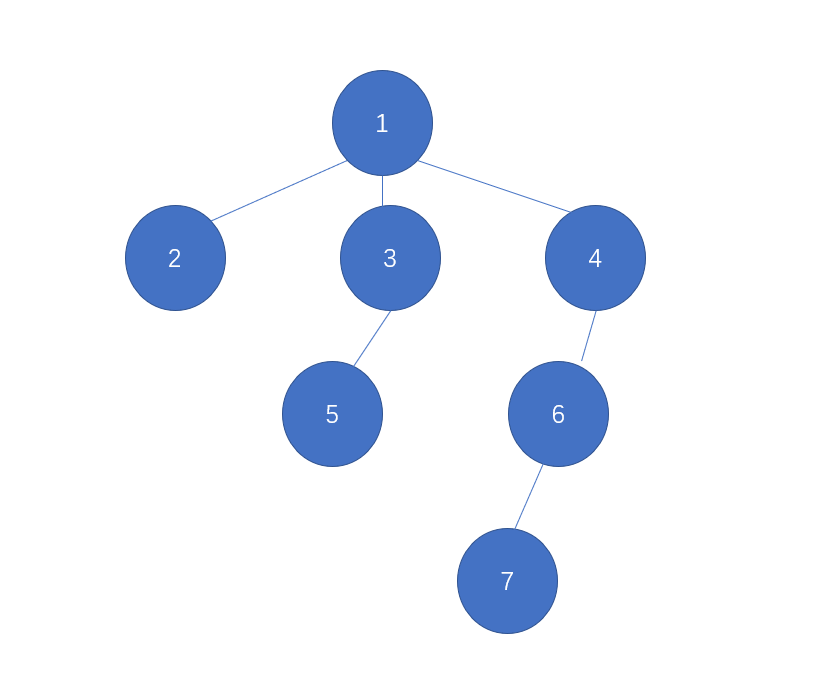
题目要求我们找出每一个叶子节点距离编号小于他的叶子节点的最小值

叶子节点很好找，就是树中出度为0的点，那么我们怎么找距离最近呢？

我们知道节点深度随着叶子节点的序号递增时递增，但是相邻的两个叶子节点的距离是否一定是最小的呢？显然不是的

 我们需要求出最小距离

以这张图为例

对于点5，我们是找点5和点2的距离 dep[1,5]+dep[1,2]

对于点7，我们是找点7和点2的距离 dep[1,7]+dep[1,2]

对于点10，我们是找点10和点7的距离 dep[6,7]+dep[6,10]

聪明的你有没有看出来，实际上我们只是需要找到，叶子节点的lca点即可！

那么我们最短的距离一定是，从底至上更新信息，当推到根节点或者走过的点的时候，当前节点的信息就是，当前点，到距离他最近的叶子节点的距离

那么第i个叶子节点的答案就是

从当前节点向上dfs，直到找到根节点或者被标记的节点为止，然后回滚，更新每个节点到距离他最近的叶子节点的距离

得到答案就是这个被标记点的到距离这个被标记点最近的叶子节点的距离+当前叶子节点到被标记点的距离

由于我们是从编号最小的叶子节点开始枚举，我们不会计算重复的情况

代码如下：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 3e6 + 5;
int n, in[maxn], out[maxn], fa[maxn], minn[maxn], vis[maxn], ans[maxn];
int dfs(int u, int cnt, int id) {
    if(vis[u]) {
        ans[id] = minn[u] + cnt;
        return minn[u] + 1;
    }
    vis[u] = 1;
    minn[u] = min(cnt, dfs(fa[u], cnt + 1, id)); //更新从下往上的值还有从上往下的值
    return minn[u] + 1;
}
int main() {
    scanf("%d", &n);
    vis[0] = 1;
    fa[1] = 0;
    for(int v = 2; v <= n; v++) {
        int u;
        scanf("%d", &u);
        out[u]++;
        fa[v] = u;
    }
    vector<int> vec;
    for(int i = 1; i <= n; i++) {
        if(out[i] == 0) {
            vec.push_back(i);
        }
    }
    minn[0] = 1e9;
    sort(vec.begin(), vec.end());
    for(int i = 0; i < vec.size(); i++) {
        dfs(vec[i], 0, i);
    }
    ans[0] = -1;
    for(int i = 0; i < vec.size(); i++) {
        printf("%d %d
", vec[i], ans[i]);
    }

}