首先来了解下一些概念性的东西。
二分图:
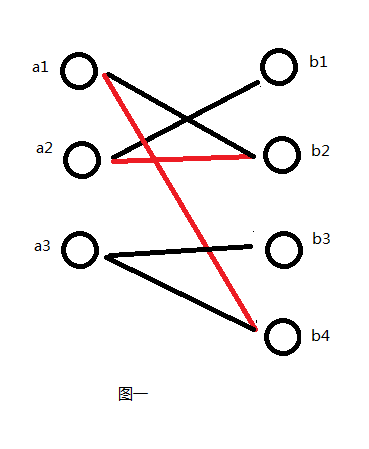
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。图一就是一个二分图。
匈牙利算法:
匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。匈牙利算法是基于Hall定理中充分性证明的思想,它是一种用增广路径求二分图最大匹配的算法。
Hall定理:
二部图G中的两部分顶点组成的集合分别为X, Y; X={X1, X2, X3,X4, .........,Xm}, Y={y1, y2, y3, y4 , .........,yn}, G中有一组无公共点的边,一端恰好为组成X的点的充分必要条件是:X中的任意k个点至少与Y中的k个点相邻。(1≤k≤m)
匹配:
给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配。图一中红线为就是一组匹配。
未盖点:
设Vi是图G的一个顶点,如果Vi 不与任意一条属于匹配M的边相关联,就称Vi 是一个未盖点。如图一中的a3、b1。
交错路:
设P是图G的一条路,如果P的任意两条相邻的边一定是一条属于M而另一条不属于M,就称P是一条交错路。如图一中a2->b2->a1->b4。
可增广路:
两个端点都是未盖点的交错路叫做可增广路。如图一中的b1->a2->b2->a1->b4->a3。
顶点的数目:
图中顶点的总数。
最大独立数:
从V个顶点中选出k个顶,使得这k个顶互不相邻。 那么最大的k就是这个图的最大独立数。
最小顶点覆盖数:
用最少的顶点数k来覆盖图的所有的边,k就是这个图的最小顶点覆盖数。
最大匹配数:
所有匹配中包含的边数最多的数目称为最大匹配数。
顶点的数目=最大独立数+最小顶点覆盖数(对于所有无向图都有效)
最大匹配数=最小顶点覆盖数(只对二分图有效)
这么多概念罗列出来了,下面放个实际中可能遇到的问题。其实就是算法竞赛中的一道题目,简化阐述下。
问题:
分析:
可以按男女画出二分图。因为要求选出的小孩都要相互认识,则可以在相互不认识的小孩之间连线,这样只要小孩之间没有线直接相连,那么他们就肯定就是相互认识的了。也就因此转化为了求这个二分图的最大独立数。
为了便于理解,首先我们来做个游戏。假设现在有5个男孩(b1,b2,b3,b4,b5)、五个女孩(g1,g2,g3,g4,g5)。b1不认识g1,g2;b2不认识g2,g3;b3不认识g2,g5;b4不认识g3;b5不认识g3,g4,g5。男孩女孩站两排,相互不认识的他们之间用一根线相连。得到的图如下:
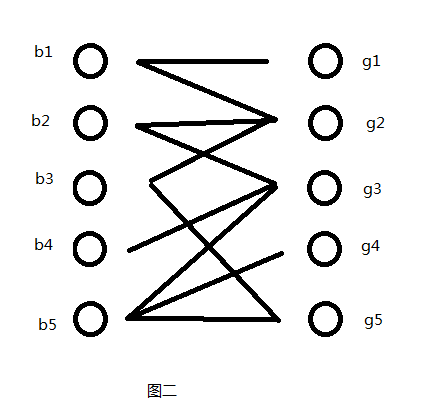
因为相互不认识的小孩之间会有一根线,所以如果我们想得到相互都认识的小孩,那么最终留下的小孩他们的手里都不能握有线了,很简单如果他们手中还有线,那就说明留下的人还有他不认识的。这样,之前的问题也就转变为了如何去除最少的小孩,使留下的小孩手中没有线。再换一种说法,也就是怎么在这么多小孩中找出最少的人,他们握有所有的线。这下就转换为了寻找最小顶点覆盖数。
这样如果找到了最小顶点覆盖数,我们又知道顶点数(所有的小孩的数目),就可以求出最大独立数(现场留下的小孩)。
又因为对于二分图,最大匹配数=最小顶点覆盖数。这个问题进而也就变成了求解最大匹配数。而匈牙利算法正是用来求最大匹配数的一个很好的方法。
下面我们就来看看匈牙利算法的具体流程。
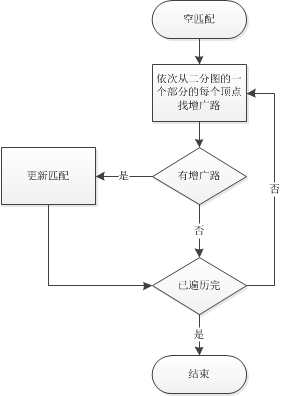
上面的流程有些抽象,具体要怎么来找增广路呢,下面给出具体操作的流程图。

是不是感觉有些乱,让我们来一步一步的分析。为了简化步骤我们用下图来分析
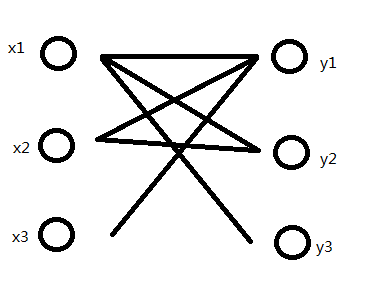
第一个最外层的循环从x1开始:
按照流程图,第一次肯定有xi了,清空标记后,yi肯定也是没有标记的了。然后对yi进行标记,第一次M自然也是空的了,M中加入(x1,y1)得到新的M{(x1,y1)},于是得到下图。

最外层循环到了x2:
好,接下来最大匹配数加1,循环继续。下面就该轮到x2了。首先清空Y的标记。
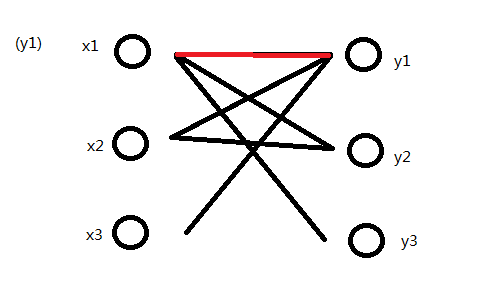
这时x2再找到y1时它已经没有标记了,这时再来标记它。但y1已经在M中了,它的对应顶点为x1。所以接下来x1要更新关联点。
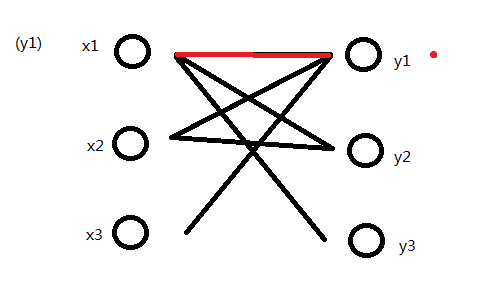
由x1开始查找时,在Y中y1已经被标记了,只能找下一个顶点,于是便找到了y2。y2未被标记,标记它。x1的关联点更新为y2,x2的关联点更新为y1。因此得新的M为{(x2,y1),(x1,y2)}
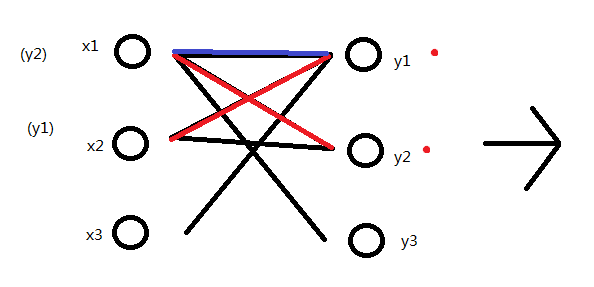
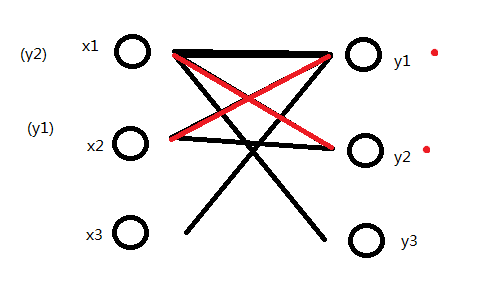
好,最大匹配数加1,循环继续。清空Y中标记。
最外层循环到了x3:

下面就轮到x3了。x3找到y1,y1未标记,标记之。
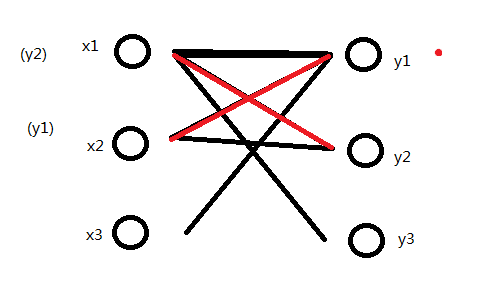
y1的关联是x2。又轮到x2找了。x2找到y1,但y1已被标记,于是便找到y2。y2未被标记,标记之。

y2的关联为x1,x1开始找。x1找到y1,y1已被标记,找到y2,y2已被标记。找到y3,y3未被标记,标记之。同时y3没有关联。更改x1的关联为y3。
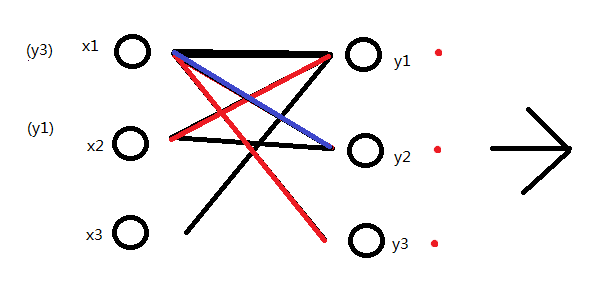
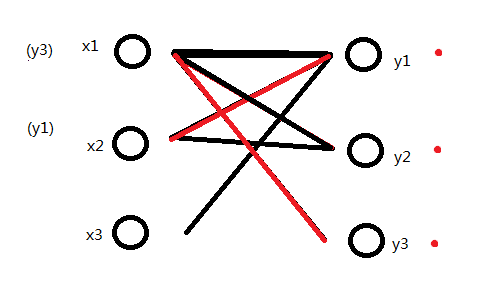
原(x1,y2)的关联也因为x1的改变,变为了(x2,y2)
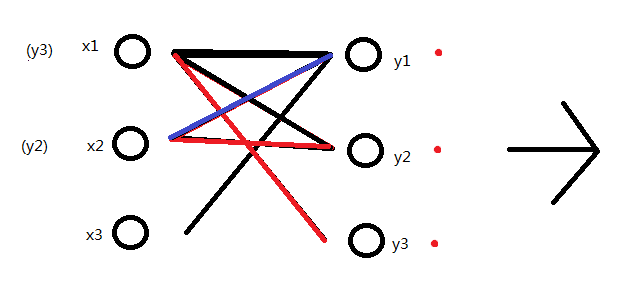
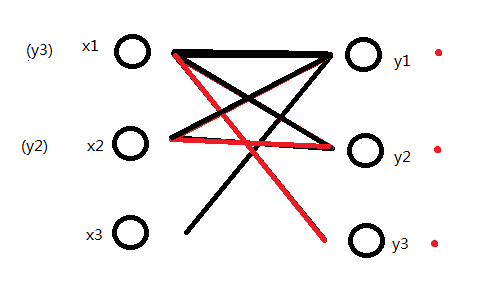
同时新增关联(x3,y1)更新M为{(x3,y1),(x2,y2),(x1,y3)}。最大匹配数加1。这时已经没有更多的X中顶点可选了。最大匹配数就这样被找出来了。
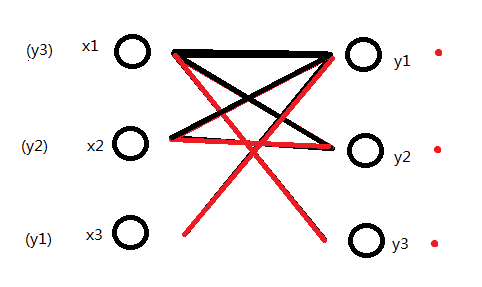
细心的人可能已经看出来了,有M'{(x2,y1),(x1,y2)},最后找出的路径x3->y1->x2->y2->x1->y3是一条增广路径。
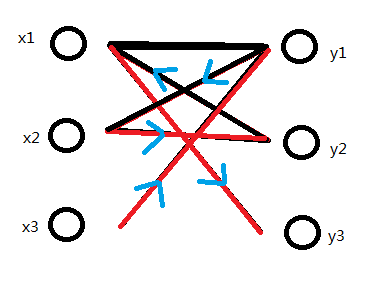
下面说一些增广路的特性,匈牙利法的正确性验证自己有兴趣可以证明下。
(1)有奇数条边。
(2)起点在二分图的左半边,终点在右半边。
(3)路径上的点一定是一个在左半边,一个在右半边,交替出现。
(4)整条路径上没有重复的点。
(5)路径上的所有第奇数条边都不在原匹配中,所有第偶数条边都出现在原匹配中。
(6)把增广路径上的所有第奇数条边加入到原匹配中去,并把增广路径中的所有第偶数条边从原匹配中删除(这个操作称为增广路径的取反),则新的匹配数就比原匹配数增加了1个。
接下来就要用计算机来实现这个算法的过程了。相信有了上面的基础,已经不难完成了。
我是用c++编译的,程序很多地方肯定还有待优化,主要是为了展示算法流程。到这里至少应该对匈牙利算法有所了解了,算法讲解到此结束。
#include <stdio.h> #include <string.h> #define MAXNUM 1000 //递归 //xi 二分图左部中的顶点 //ytotal 二分图右部顶点总数 //relation xy之间的关联关系 //link xy之间的匹配 //y的标记 bool recursion(const int xi, const int ytotal, const bool relation[][MAXNUM], int link[], bool* sign) { for(int i = 0; i < ytotal; i++) { if(relation[xi][i] && !sign[i])//有关联并且没被标记 { sign[i] = true;//标记 if(link[i] == -1 || recursion(link[i], ytotal, relation, link, sign))//y没有有匹配则更新y的匹配;y有匹配则用它的匹配继续查找 { link[i] = xi;//更新y的匹配 return true; } } } return false; } //匈牙利算法 //xtotal 二分图的左部包含顶点总数 //ytotal 二分图的右部包含顶点总数 //xy之间的关联 int Hungary(const int xtotal, const int ytotal,const bool relation[][MAXNUM]) { int link[MAXNUM][2];//与y匹配的x memset(link, -1, sizeof(link)); int cnt = 0;//最大匹配数 for(int i = 0; i < xtotal; i++) { bool sign[MAXNUM] = {false};//清空标记 if(recursion(i, ytotal, relation, link[i], sign))//寻找增广路径 { cnt++; } } return cnt; } int main(int argc, char** argv) { while(true) { int boytotal = 0; int girltotal = 0; bool relation[MAXNUM][MAXNUM] = {false}; //获取男孩总数 do { fflush(stdin); printf("请输入男孩总数(不大于%d): ", MAXNUM); scanf("%d",&boytotal); }while(0 == boytotal || boytotal > MAXNUM); printf("男孩总数输入成功。 "); printf("------------------------ "); //获取女孩总数 do { fflush(stdin); printf("请输入女孩总数(不大于%d): ", MAXNUM); scanf("%d",&girltotal); }while(0 == girltotal || girltotal > MAXNUM); printf("女孩总数输入成功。 "); printf("------------------------ "); //获取相互不认识的男女 do { int boyno = 0; int girlno = 0; fflush(stdin); printf("请输入相互不认识的异性小孩,如第一个男孩不认识第二个女孩则输入1,2: "); scanf("%d,%d",&boyno, &girlno); if(boyno>0&&boyno<=boytotal&&girlno>0&&girlno<=girltotal) { relation[boyno-1][girlno-1] = true; char ret = '�'; fflush(stdin); printf("一对互不认识的男女输入成功,是否结束输入?(Y/N) "); scanf("%c",&ret); if('Y' == ret || 'y' == ret) { break; } } }while(true); printf("------------------------ "); printf("男孩个数:%d;女孩个数:%d;小孩总数:%d ",boytotal,girltotal,boytotal+girltotal); //寻找最大匹配 int tmp = Hungary(boytotal, girltotal, relation); printf("最大匹配数:%d ", tmp); printf("最多可以留下人数:%d ", boytotal+girltotal-tmp); printf("------------------------ "); char ret; fflush(stdin); printf("是否退出?(Y/N) "); scanf("%c",&ret); if('Y' == ret || 'y' == ret) { break; } printf("------------------------ "); } return 1; }