c++<cstdlib>文件中的函数产生随机数

  C++中没有自带的random函数，要生成随机数就需要用c文件"stdlib.h"里的函数rand()和srand()，不过，由于rand()的内部实现是用线性同余法做的，

  所以生成的并不是真正的随机数，而是在一定范围内可看为随机的伪随机数，下面分别介绍一下各自的用法

1. int rand(void)；它是无参函数，返回int型数据，并且返回值范围是 0~RAND_MAX(32767)，RAND_MAX定义在头文件 <cstdlib>中，是一个8位数；

    rand()的作用是用来产生随机数序列的，它产生的随机数是根据种子生成的，不同的种子产生的随机序列也是不同的；而系统默认的种子是1，如果

    你没有设置种子的话，那每次使用rand()产生的随机序列都是固定的，它会产生相同的随机序列，所以这不是真正的随机，而是伪随机数，要做到真正

    的随机，就要使种子随机。下面先说一下rand()的用法，后面再说怎么设置随机种子，上代码

#include<iostream>
#include<ctime>
#include<cstdlib>
using namespace std;
int main()
{
    cout<<"第一次产生的随机序列：";
    for(int i=1;i<=10;i++)
        cout<<rand()<<" ";
    cout<<"
";
    return 0;
}

我运行了两次程序，分别产生了两个随机序列，如图

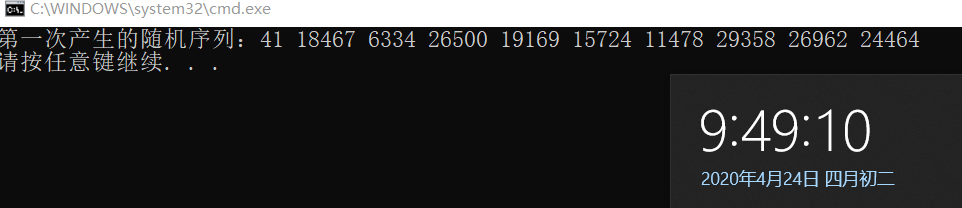
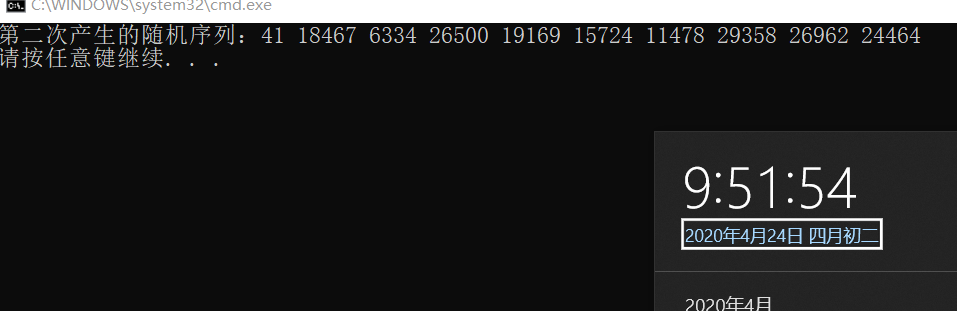
你会发现两次所生成的随机序列是相同的，这是为啥 ？上面说过系统默认的种子是1，而你又没有设置随机种子，所以每次产生的随机序列都是一样的，是伪随机。

如何解决这个伪随机的问题呢，这就引出了srand()。

2. void srand(unsigned int seed)；srand()就是用来设置rand()函数的种子的，若srand()每次设置的种子不同，那么rand()就会产生不同的随机序列。一般用时间来

    做种子，因为时间一直在变，这样种子就会不同，从而可以产生真正的随机数。方法为将函数time(0)作为srand()的参数(因为time会有返回值，实际上是让这个返回值做参数)，

    另外srand(time(0))只需要执行一次就行了。具体操作还是看代码吧

#include<iostream>
#include<ctime>
#include<cstdlib>
using namespace std;
int main()
{
    srand((int)time(0));  //用时间做种子
    cout<<"第2次产生的随机序列：";
    for(int i=1;i<=10;i++)
        cout<<rand()<<" ";
    cout<<"
";
    return 0;
}

还是运行了两次程序，分别产生了两个随机序列，结果如下图

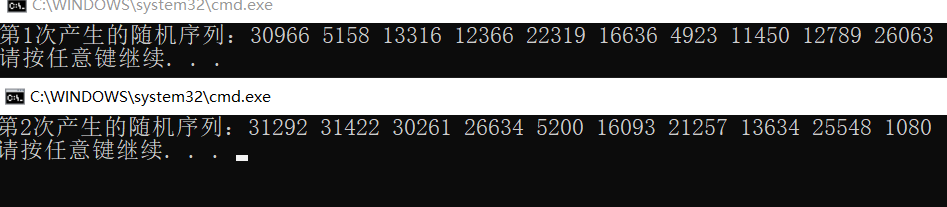
 那你会发现这两次产生的两个随机序列是不一样的，因为用了时间做种子。下面还有一个小问题，就是如果要产生某个范围内的随机数要怎么实现呢，比如

 要产生[0,100)这个范围内的随机数，或者[0,10000)这个范围内的随机数，就要用rand()%n来产生[0,n)这个范围内的随机数了。用rand()%(b-a)+a 来产生[a,b)

 这一范围内的随机数，下面用程序分别模拟一下这三种情况：

#include<iostream>
#include<ctime>
#include<cstdlib>
using namespace std;
int main()
{
    srand((int)time(0));  //用时间做种子
    cout<<"产生[0,100)内的随机数：";
    for(int i=1;i<=10;i++)
        cout<<rand()%100<<" ";
    cout<<"
";
    cout<<"产生[0,10000)内的随机数：";
    for(int i=1;i<=10;i++)
        cout<<rand()%10000<<" ";
    cout<<"
";
    cout<<"产生[100000,1000000)内的随机数：";
    for(int i=1;i<=10;i++)
        cout<<rand()%(1000000-100000)+100000<<" ";
    return 0;
}

结果如下图：

通过上面的操作就可以产生指定范围内的随机数了。

产生一定范围内的随机数的公式是：

要产生 [0,n) 内的随机数，用 rand()%n

要产生 [a,b) 内的随机数，用 rand()%(b-a)+a

要产生 [a,b] 内的随机数，用 rand()%(b-a+1)+a

要产生 (a,b] 内的随机数，用 rand()%(b-a)+a+1

通用公式为：a + rand() % n；其中的a是起始值，n是整数的范围，就是a~n之间的随机数。

参考：https://www.cnblogs.com/VVingerfly/p/5990714.html

           https://www.cnblogs.com/xiaokang01/p/9786751.html#_label0_2