WebGL入门教程(三)-webgl动画

前面文章：

WebGL入门教程(一)-初识webgl

WebGL入门教程(二)-webgl绘制三角形

WebGL动画有移动、旋转和缩放，我们将移动、旋转和缩放图形，然后将其绘制到屏幕上，称为变换(transformations)或者仿射变换(affine transformations).

1.移动

效果图：

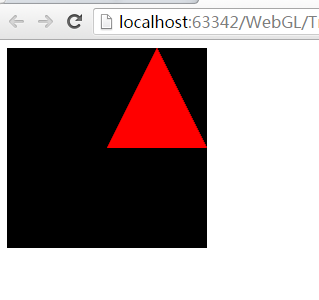
1.1在WebGL入门教程(二)-webgl绘制三角形的基础上进行修改，原理就是，三个顶点的坐标（x,y,z）同时发生了变化，重新计算三个坐标值；

//顶点着色器程序
    var VSHADER_SOURCE =
        "attribute vec4 a_Position;" +
        "uniform vec4 u_Translation;" +
        "void main() {" +
            //设置坐标
        "gl_Position = a_Position + u_Translation; " +
        "} ";

从上面可以看到，顶点增加了一个变量平移距离u_Translation，然后将平移距离传输给定点着色器；

//声明偏移变量
var Tx = 0.5,Ty = 0.5,Tz = 0.0;

//将平移距离传输给定点着色器
 var u_Translation = gl.getUniformLocation(shaderProgram,'u_Translation');

 gl.uniform4f(u_Translation,Tx,Ty,Tz,0.0);

 1.2还有一种表达方式，就是用变形矩阵进行计算坐标。

 经过计算得出平移矩阵公式（这是行主序，但是在写代码的时候就是列主序了）：

 

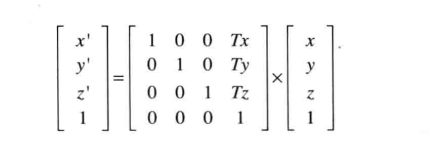
什么是列主序：

例如一个坐标点 V(x,y,z,w)，其实是以列的形势存储的。

[x]

[y]

[z]

[w]

刚才得到的公式是行主序的，所以，一定要灵活变通。

得出x'=x+Tx;y'=y+Ty;z'=z+Tz;

由上面的公式就开始写代码吧：首先就是顶点着色器的更改,<新坐标>=<矩阵>*<旧坐标>，得出下面代码；

var VSHADER_SOURCE =
        "attribute vec4 a_Position;" +
        "uniform mat4 u_xformMatarix;" +
        "void main() {" +
            //设置坐标
        "gl_Position = u_xformMatarix * a_Position;" +
        "} ";

然后将矩阵传输给定点着色器；

var Tx = 0.5,Ty = 0.5,Tz = 0.0;
//注意WebGL的矩阵式列主序的
var xformMatrix = new Float32Array([
        1.0, 0.0, 0.0, 0.0,
        0.0, 1.0, 0.0, 0.0,
        0.0, 0.0, 1.0, 0.0,
        Tx, Ty, Tz, 1.0
    ]);
//然后将矩阵传输给定点着色器
 var u_xformMatarix = gl.getUniformLocation(shaderProgram,'u_xformMatarix');
 gl.uniformMatrix4fv(u_xformMatarix, false, xformMatrix);

uniformMatrix4fv方法参数的讲解，

第一个参数：代表uniform变量的存储位置；

第二个参数：在WebGL中指定为false；

第三个参数：待传输的类型化数组；

2.旋转 

效果图：

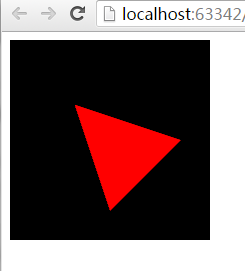
2.1同理，旋转也需要计算旋转之后三个坐标的值，不过它的要求就高了， 需要知道旋转轴，旋转方向和旋转角度。

这是就需要数学知识了

//顶点着色器程序
    var VSHADER_SOURCE =
        "attribute vec4 a_Position;" +
        "uniform float u_CosB,u_SinB;" +
        "void main() {" +
            //设置坐标
        "gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;" +
        "gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;" +
        "gl_Position.z= a_Position.z;" +
        "gl_Position.w = 1.0;" +
        "} ";

从上面可以看到，顶点着色器定义了正弦值，余弦值，然后根据得到的值或得坐标值，，然后将旋转图形所需的数据传输给定点着色器

//旋转角度
var ANGLE = 45.0;

// 将旋转图形所需的数据传输给定点着色器
var radian = Math.PI*ANGLE/180.0;//转化为弧度
var cosB = Math.cos(radian);
var sinB = Math.sin(radian);

var u_CosB = gl.getUniformLocation(shaderProgram,'u_CosB');
var u_SinB = gl.getUniformLocation(shaderProgram,'u_SinB');

gl.uniform1f(u_CosB,cosB);
gl.uniform1f(u_SinB,sinB);

2.2 经过计算得出旋转矩阵公式（这是行主序，但是在写代码的时候就是列主序了）：

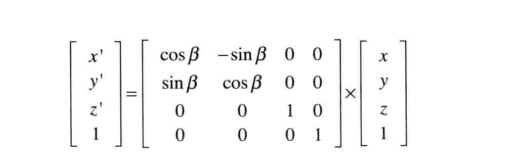
由上面的公式就开始写代码吧：首先就是顶点着色器的更改,<新坐标>=<矩阵>*<旧坐标>，得出下面代码；

var VSHADER_SOURCE =
        "attribute vec4 a_Position;" +
        "uniform mat4 u_xformMatarix;" +
        "void main() {" +
            //设置坐标
        "gl_Position = u_xformMatarix * a_Position;" +
        "} ";

然后将矩阵传输给定点着色器；

var xformMatrix = new Float32Array([
       cosB, sinB, 0.0, 0.0,
      -sinB, cosB, 0.0, 0.0,
       0.0, 0.0, 1.0, 0.0,
       0.0, 0.0, 0.0, 1.0
    ]);
    var u_xformMatarix = gl.getUniformLocation(shaderProgram,'u_xformMatarix');
    gl.uniformMatrix4fv(u_xformMatarix, false, xformMatrix);

3.缩放

效果图：

直接来看矩阵表示吧，毕竟以后都是用矩阵的，

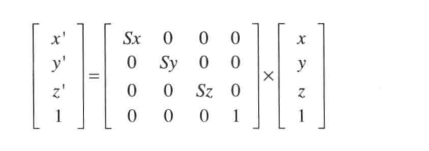
主需要更改传输到顶点时的代码

 var Sx = 1.0;Sy =1.5; Sz = 1.0;
    var xformMatrix = new Float32Array([
        Sx, 0.0, 0.0, 0.0,
        0.0, Sy, 0.0, 0.0,
        0.0, 0.0, Sz, 0.0,
        0.0, 0.0, 0.0, 1.0
    ]);
    var u_xformMatarix = gl.getUniformLocation(shaderProgram,'u_xformMatarix');
    gl.uniformMatrix4fv(u_xformMatarix, false, xformMatrix);

*以上摘至《WebGL编程指南》